这里对2010年至今的微软笔试题做了一个汇总和分类，然后进行了解答和分析，每一类题中涉及到的知识点和方法在很多别家公司的笔试面试中也有用，希望下面的内容能在大家找工作的时候给大家一些帮助。

1 、数组，排序相关

1 、 合并两个已排好序的数组在最坏情况下需要比较多少次？ （ 2010 年 9 月校招考题）

(A)2n (B)2n-1 (C)2n+1 (D)2n-2 (E)None of above

分析：最后所生成的数组元素个数为 2n 个 . 最坏情况为 : 每比较一次 , 只确定一个元素的位置 ( 最后一次比较确定两个元素的位置 , 即倒数第一个和倒数第 2 个 ), 所以总的最坏比较次数为 2n-1.

2、 编程题 （ 2010 年 9 月校招考题）

一个 rotated sorted array 是一个在某处交换了元素的 sorted array ，例如， rotated sorted array[13, 27, 37, 2, 3, 5] 是从 sorted array[2, 3, 5, 13, 27, 37] 变换而来的，这个 sorted array 是以增序排好序的。

现在需要计算给定值在 rotated sorted array 中的索引。例如， 27 在 rotated sorted array[13, 27, 37, 2, 3, 5] 中的索引是 2 。注意：如果想得满分，程序的时间复杂度需要小于 O(n) 。

分析：旋转数组求下标问题。

如果数组是有序数组，进行二分查找的时间复杂度是 O(logN) 。在旋转数组中，二分查找的情况稍微复杂一些，如下图所示，数组平分后一半是有序数组，一半仍是旋转数组。

确定下次二分查找在前半段区间还是后半段区间进行。
仔细分析该问题，可以发现，每次根据 low 和 high 求出 mid 后， mid 左边（ [low, mid] ）和右边（ [mid, high] ）至少一个是有序的。
a[mid] 分别与 a[left] 和 a[right] 比较，确定哪一段是有序的。
如果左边是有序的，若 x 且 x>a[left], 则 right=mid-1 ；其他情况， left =mid+1 ；
如果右边是有序的，若 x> a[mid] 且 x 则 left=mid+1 ；其他情况， right =mid-1 ；

代码如下：

[cpp] view plain copy

1. int binary_search_rotate_arry( int *a, int n, int x)

2. {

3. int low = 0, high = n - 1, mid;

4. while (low <= high)

5. {

6. mid = low + ((high - low) >> 1);

7. if (a[mid] == x)

8. return mid;

9. if (a[mid] >= a[low])

10. { //左边有序

11. if (x = a[low])

12. high = mid - 1;

13. else

14. low = mid + 1;

15. }

16. else //右边有序

17. {

18. if (x > a[mid] && x <= a[high])

19. low = mid + 1;

20. else

21. high = mid - 1;

22. }

23. //cout <

24. }

25. return -1;

26. }

3 、 一个文件中有多行信息，每一行信息中，第一个为一个 key ，后面用空格间隔若干 symbol ，例如：

B A C D E （每一行中的一个 symbol 至多出现一次，且不与 key 重复），表示 B 关联。

若一行中只有一个值，如 C 则表示无关联。

现在求写出一个算法，判断一个文件下的所有行中所包含的关联，能否囊括所有元素的关联，使之形成一个 sort 链，达到例如： A 的效果。

例 1

input:

A B C

B C

C

（ means:A ）

output ：

It can be sorted determine.

例 2

input:

A B

B A

C

（ means:A ）

output:

It can't be sorted determine.

例 3

input:

A B

A C

C

(means:A

output:

It can't be sorted determine.

分析：貌似是拓扑排序的一道题，这个博主不懂，大家补充，多谢。

4、数组中最大连续子段和问题，求其最优算法的时间复杂度   （ 2011 年 4 月实习招聘考题）

分析：典型的动态规划问题

若记 b[j]=max(a[i]+a[i+1]+..+a[j]), 其中 1<=i<=j, 并且 1<=j<=n 。则所求的最大子段和为 max b[j] ， 1<=j<=n 。

由 b[j] 的定义可易知，当 b[j-1]>0 时 b[j]=b[j-1]+a[j] ，否则 b[j]=a[j] 。故 b[j] 的动态规划递归式为 : b[j]=max(b[j-1]+a[j],a[j]) ， 1<=j<=n 。

据此，可设计出求最大子段和问题的动态规划算法如下：

[cpp] view plain copy

1. /**********************************************************************

2. 动态规划求最大子序列和

3. **********************************************************************/

4. int Maxsum( int * arr, int size)

5. {

6. int maxSum = -INF; //很重要，初始值赋值为负无穷大

7. int sum = 0;

8. for ( int i = 0; i

9. {

10. //小于0则舍弃

11. if (sum

12. {

13. sum = arr[i];

14. } else

15. {

16. sum += arr[i];

17. }

18. //比现有最大值大，则替换

19. if (sum > maxSum)

20. {

21. maxSum = sum;

22. }

23. }

24. return maxSum;

25. }

只用到了 O(n) 的时间复杂度和 O(1) 的空间复杂度。

5 、 快排的最优、最坏、平均的复杂度  （ 2011 年 4 月实习招聘考题）

分析：基础题。最优、平均： O( n log n) ，最坏： O(n^2)

6 、 找出一个数组中，第 M 大的数，时间复杂度是？

A O(logN)

B O(N)

C O(NlogN)

D O(N2) /* （代表平方） */

E 以上都不对

分析： 1 ） 利用快速排序的思想，从数组 S 中随机找出一个元素 X ，把数组分为两部分 Sa 和 Sb 。 Sa 中的元素大于等于 X ， Sb 中元素小于 X 。这时有两种情况：

1. Sa 中元素的个数小于 k ，则 Sb 中的第 k-|Sa| 个元素即为第 k 大数；

2. Sa 中元素的个数大于等于 k ，则返回 Sa 中的第 k 大数。时间复杂度近似为 O(n)

2 ） 利用 hash 保存数组中元素 Si 出现的次数，利用计数排序的思想，线性从大到小扫描过程中，前面有 k-1 个数则为第 k 大数，平均情况下时间复杂度 O(n)

7 、 给出一个一维的点集，求能够包含 [n/2] 个点的第一个最小区间的左边界和右边界（实际上就是数组） 。例如 {5,-3,10 ， 4 ， -2 ， -5} ，第一个包含 [n/2] 个点的最小区间就是 [-5,-2] 。（ 2011 年 4 月实习招聘考题）

分析：这道题目让求解的是前n/2 个数，也就是说，我们找到中位数和最大 ( 小 ) 元素即可。而求中位数的方法，在数组有序的时候显然是二分，但这里的数组是无序的，恩，要时刻记得快排的 partition 算法，在很多时候很有帮助。代码如下：

[cpp] view plain copy

1. int Partition( int * A, int begin, int end)

2. {

3. //分治元素

4. int X = A[end];

5. //A[begin]...A[i-1]

6. int i=begin;

7. //A[j]...A[end]>=X

8. int j=end;

9. //循环开始前A[j]是等待被填充的元素，该元素已被保存到X

10. while (i

11. {

12. //从前面开始找到小于X的数

13. while (A[i]

14. i++;

15. //A[j]被填充，A[i]等待被填充

16. if (i

17. A[j] = A[i];

18. while (A[j]>=X && i

19. j--;

20. //A[i]被填充，A[j]等待被填充

21. if (i

22. A[i]=A[j];

23. }

24. A[i] = X;

25. return i;

26. }

27. /*

28. 返回中位数元素

29. @para:

30. A[begin...end]为所求数组

31. middle_index 为中位数的索引

32. middle_element为中位数元素，返回用

33. */

34. void FindMiddleElement( int * A, int begin , int end,

35. int middle_index, int & middle_element)

36. {

37. if (!A || begin>end)

38. {

39. return ;

40. }

41. int split_pos = Partition(A,begin,end);

42. if (split_pos == middle_index)

43. {

44. middle_element = A[split_pos];

45. return ;

46. }

47. FindMiddleElement(A,begin,split_pos-1,middle_index,middle_element);

48. FindMiddleElement(A,split_pos+1,end,middle_index,middle_element);

49. }

8、 N 个数，范围从 -N 到 N, 可能重复，排序时间复杂度最好能到多少？ （ 2011 年 9 月招聘考题）

分析：答案是O(n) ，使用 计数排序和位图排序，桶排序都可以达到这个时间复杂度。

9 、 假设一个 长度为 80 的数组 选择排序已完成主循环 32 次迭代。现在 能保证有多少元素 是在他们 最终的位置 ？ （ 2012 年 4 月实习生招聘考题）

A 、 16    B 、 31 C 、 32 D 、 39   E 、 40

分析：这个不用过多解释吧，对选择排序不了解的详见找工作知识储备 (3)--- 从头说 12 种排序算法：原理、图解、动画视频演示、代码以及笔试面试题目中的应用

10 、下列哪项陈述是对的？ （ 2012 年 4 月实习招聘考题）

A 、我们能从一颗二叉树的先序遍历序列和中序遍历序列，确定这颗二叉树。

B 、我们能从一颗二叉树的先序遍历序列和后序遍历序列，确定这颗二叉树。

C 、近乎排序的数组，插入排序可以比快排更有效。

D 、假设 T(n) 是解决 n 个元素的问题时候的运行时间， T(N)= O(1) 如果 n = 1 ； T(n) ＝ 2×T(N/2)+ O(n) 当 n ＞ 1 ；则 T(n) 是 O(nlgn)

E 、上述都不对

11 、下面哪项 ( 些 ) 陈述是对的？ （ 2012 年 4 月实习招聘考题）

A 、插入排序和冒泡排序 在 大型数据集 下效率很低 。

B 、快速排序是在最坏情况 下 比较 了 O （ N^2 ） 次 。

C 、有一 序列 7,6,5,4,3,2,1 。如果使用选择排序（升序），交换操作 次 数是 6

D 、堆排序使用两个堆操作：插入、堆调整

E 、 上述都不对

分析：常规题，对各种排序算法要熟悉

12 、 最长递增子序列（ LIS ）是一个序列 满足 元素的值不断增加 的子序列中最长的序列 。

例如，里 { 2,1,4,2,3,7,4,6 } 是 { 1,2,3,4,6 } ，以及 LIS 的长度为 5 。

考虑具有 n 个元素的数组， 则得到 LIS 的长度 的 最低的时间复杂度和空间复杂度 是多少 ？（ 2012 年 4 月实习招聘考题）

A 、 Time : N^2 , Space : N^2
B 、 Time : N^2 , Space : N
C 、 Time : NlogN , Space : N
D 、 Time : N , Space : N
E 、 Time : N , Space : C

分析：详见找工作知识储备 (2)--- 数组字符串那些经典算法：最大子序列和，最长递增子序列，最长公共子串，最长公共子序列，字符串编辑距离，最长不重复子串，最长回文子串

13 、对于以下的定义 （ 201 3 年 4 月实习招聘考题）

[cpp] view plain copy

1. int [][] myArray3 = new int [3][]{

2. new int [3]{5,6,2},

3. new int [5]{6,9,7,8,3},

4. new int [2]{3,2}};

则 myArray3[2][2] 返回的是 ?

A. 9

B. 2

C. 6

D. overflow

分析：越界导致overflow

14 、以下哪些 排序方法是稳定的？ （ 201 3 年 4 月实习招聘考题）

A. 冒泡排序

B. 快速排序

C. 堆排序

D. 归并排序

E. 选择排序

15 、 快速排序的最好时间复杂度是 ? （ 2013 年 9 月招聘考题）

A 、 O(lgn)
B 、 O(n)
C 、 O(nlgn)
D 、 O(n*n)

分析：好吧，这一题就不解释了，大家都知道的。

2 、链表相关

1 、下列程序的输出是什么？ （ 2012 年 4 月实习招聘考题）

[cpp] view plain copy

1. #include

2. using namespace std;

3. struct Item

4. {

5. char c;

6. Item *next;

7. };

8. Item *Routine1(Item *x)

9. {

10. Item *prev = NULL,

11. *curr = x;

12. while (curr)

13. {

14. Item *next = curr->next;

15. curr->next = prev;

16. prev = curr;

17. curr = next;

18. }

19. return prev;

20. }

21. void Routine2(Item *x)

22. {

23. Item *curr = x;

24. while (curr)

25. {

26. cout< c<< " " ;

27. curr = curr->next;

28. }

29. }

30. int main( void )

31. {

32. Item *x,

33. d = { 'd' , NULL},

34. c = { 'c' , &d},

35. b = { 'b' , &c},

36. a = { 'a' , &b};

37. x = Routine1( &a );

38. Routine2( x );

39. return 0;

40. }

A 、 c b a d

B 、 b a d c

C 、 d b c a

D 、 a b c d

E 、 d c b a

分析：原程序将链表进行翻转了

2 、链表和数组的区别是 ? （ 201 3 年 4 月实习招聘考题）

A. Search complexity when both are sorted

B. Dynamically add/remove

C. Random access efficiency

D. Data storage type

分析：之前看这道题的D选项是有争议的，我这里根据自己的理解还是选上吧

3 、 给定一个链表 L: (L0 , L1 , L2...Ln-1 , Ln). 写程序使得链表中的节点变为 (L0 , Ln , L1 , Ln-1 , L2 , Ln-2...). （ 201 3 年 9 月招聘考题）

[cpp] view plain copy

1. struct Node

2. {

3. int val_;

4. Node* next;

5. };

要求：

1 ） 空间复杂度 O(1) 2 ）节点中只有 next 域可以改动

分析：其实就是把链表的后半部分翻转，之后再对前半部分和后半部分做一个交叉合并就可以了吧。代码如下：

[cpp] view plain copy

1. //完成对头为head的链表的反转

2. Node* ReverseList(Node*& head)

3. {

4. if ( (head == 0) || (head->next == 0) ) return ; // 边界检测

5. Node* pNext = 0;

6. Node* pPrev = head; // 保存链表头节点

7. Node* pCur = head->next; // 获取当前节点

8. while (pCur != 0)

9. {

10. pNext = pCur->next; // 将下一个节点保存下来

11. pCur->next = pPrev; // 将当前节点的下一节点置为前节点

12. pPrev = pCur; // 将当前节点保存为前一节点

13. pCur = pNext; // 将当前节点置为下一节点

14. }

15. Return Pcur;

16. }

17. //查找中间节点，使用一快一慢两指针，快指针一次走两步，慢指针一次走一步，最后返回慢指针

18. .Node * GetMiddleNode(Node*& head)

19. {

20. if ( (head == 0) || (head->next == 0) )

21. return NULL;

22. Node* pFast = head; //快指针

23. Node* pSlow = head; // 慢指针

24. while （pFast ！= Null && pFast->next != Null）

25. {

26. pFast = pFat->next->next;

27. pSlow = pSlow->next;

28. }

29. return pSlow;

30. }

31. // 交叉合并A和B两链表

32. Node* Merge(Node* & A,Node* & B)

33. {

34. Node *p,*q,*s,*t;

35. p=A->next;

36. q=B->next;

37. while (p&&q)

38. {

39. s=p->next;

40. p->next=q;

41. if (s)

42. {

43. t=q->next;

44. q->next=s;

45. }

46. p=s;

47. q=t;

48. }

49. return A;

50. }

51. //完成题目要求的顺序调整

52. Node* ReorderList(Node* pHead)

53. {

54. Node *pMiddle, *pEnd, *nHead;

55. pMiddle =  GetMiddleNode(Node*& head);

56. pEnd = ReverseList(pMiddle); //后半部分反转

57. nHead = Merge(pHead , pMiddle); //链表交叉归并

58. return nHead;

59. }

3 、 树，遍历

1 、 二叉树的任意两个节点间有一个唯一路径，求出 n 个节点的二叉树的最长路径的两个节点的最优算法时间复杂度是多少 （ 2011 年 4 月实习招聘考题）

分析：O(n) 就够了 :

从叶子节点开始，找到每个结点的经过它能得到的最长路径和它的最长分支，

(node1)

e1/         \e2

(node2)    (node3)

很明显，经过 node1 的最长路径为 node2 和 node3 的最长分支之和再加上两条边（ e1 和 e2 ）的长度 。

对这道题，多说两句，编程之美 3.8 有过解答，时间复杂度为 O(v) 。但是这里有点不同：树的边有权值。

第一种解法：最大距离的节点一定是叶子节点，首先将二叉树看成一个连通图，首先应该求根节点到所有叶节点的最大距离叶节点 A ，然后求 A 到所有其他节点的最大距离。假设要求节点 A 到其他节点之间的最长路径，题目的转换为求解以 A 为源点的最长路径。采用单源最短路径（ dijkstra ）的思想求解。这里要求最长路径，因此，每次选择时，应该从未知最大距离的节点集合中选择最大距离的节点加入已知最大距离的节点集合。如果采用堆结构来维护未知节点到 A 的最大距离，那么时间复杂度为 O （ vlogv ）。

第二种解法：采用编程之美 3.8 节的递归方法，递归遍历二叉树一次，得出最大距离，时间复杂度为 O （ v ）

思路：对于一路径，其有两种情况

1. 经过根节点，

2. 不经过根节点，

首先来考虑经过根节点的情况，这样把路径分成两部分，一是左子树起点为根节点的最长路径，

二是右子树起点为根节点的最长路径。

从根节点开始的最长路径可以通过遍历该树的叶子节点得到。

然后再考虑不经过根节点的情况，

不经过根节点，那么最长路径要不存在于左子树，要么存在于右子树。这样，我们就把问题

分解成了两个小问题，即取左子树最长路径和右子树最长路径的最大值。

现在，来分析算法复杂度，不妨记二叉树有 n 个节点，其复杂度为 f(n).

经过根节点的复杂度为 O(n) ，因为其必须遍历所有叶子节点，因此必须遍历所有的节点。

不经过根节点的复杂度为 2*f(n/2) ，假设左子树和右子树的节点数目相同。从而得到：

f(n) = O(n) + 2*f(n/2)

= O(nlogn)

2 、 后续遍历的二叉树： DEBFCA ，则下列中可能是其前序排列的是？ （ 2011 年 4 月实习招聘考题）
A ： ABFCDE
B ： ADBFEC
C ： ABDECF
D ： ABDCEF
E ： none of the above

3 、一颗 3 阶 B 树有 2047 个 key-words ，那这颗树的高度最大为多少？（ 2012 年 4 月实习招聘考题）

A 、 11 B 、 12     C 、 13    D 、 14
分析： m 阶 B- 树的根节点至少有两棵子树，其他除根之外的所有非终端节点至少含有 m/2( 向上取整 ) 棵子树，即至少含有 m/2-1 个关键字。 要想让3 阶的 B- 树达到最大的高度，那么每个节点含有一个关键字，即每个节点含有 2 棵子树，也就是所谓的完全二叉树了，这样达到的高度是最大的。即含有 2047 个关键字的完全二叉树的高度是多少。很明显求得高度是 11 。

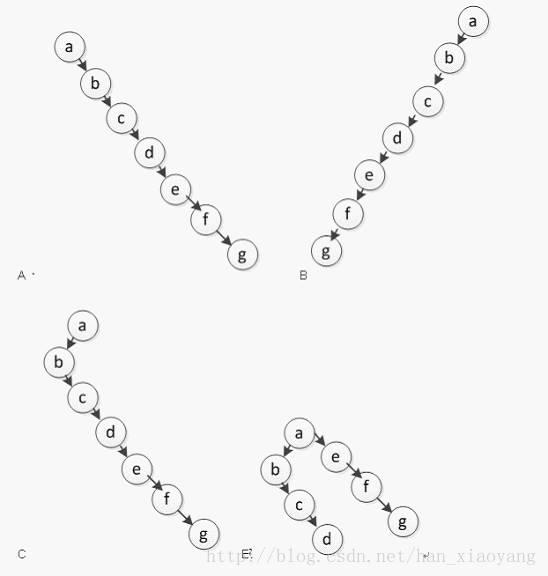
4 、 二叉树的 先序遍历结果 为 abcdefg ，则它的 中序遍历结果 可能是？ （ 2012 年 9 月招聘考题）

A 、 abcdefg
B 、 gfedcba
C 、 efgdcba
D 、 bceadfg
E 、 bcdaefg

分析：几种遍历方式，年年考，要特别注意。

5 、有 n 个元素的完全二叉树的深度是：（ 2012 年 9 月招聘考题）

A. D(n)=log2(n)

B. D(n)=1+log2(n)

C. D(n)=n+log2(n)

D. D(n)=1+n*log2(n)

分析：普遍来说，认为根结点深度为 1 ，所以深度 =1+ log2(n)

6 、我们在得知下列哪些选项的条件下可以还原 二叉树？

A. 先序遍历和中序遍历

B. 先序遍历和后序遍历

C. 中序遍历和后序遍历

D. 后序遍历

分析：一定要有一个中序遍历，才便于区分左侧和右侧部分。先序遍历和后续遍历无法确定一颗二叉树。

7 、 50 万个学生信息，其中有 id 和 name 字段， id 是 7 为数字， name 是字符串；问如果要查询 1) 通过 name 查 id 2) 通过 id 查 name 那么，合适的数据结构是 ? （ 2013 年 9 月招聘考题）

A. 1 ）叶子节点为 hash(100 bucket) 的树 2 ）叶子节点为链表的树

B. 1 ）叶子节点为链表的树 2 ）数组

C. 1 ）叶子节点为链表的树 2 ） hash(10000 bucket)

D. 1 ）排序链表 2 ）数组

分析：名字可能重复，而编号不会重复。查找名字用二叉查找树，找到节点后，会有若干个编号，所以每个节点存一个单链表。如果查找名字，编号是无重复的，有 50 万个， 10000 个桶不够用，直接用数组比较好。

4 、堆栈性质

1 、 有一个序列的 n 个数字 为 1,2,3 ， …… ， n ，现有一个 栈 最多 可以保持 M 个数 。将 N 个数 依次 进栈后，随机 弹出生成 序列。 例 设 n 为 2 ， m 为 3 ，输出序列可以 是 1 2 或 2 1 ，所以我们得到了 2 种不同的序列。设 n 是 7 ，和 m 是 5 ，请选择该栈的 可能出栈 序列。（ 2012 年 4 月实习招聘考题）

A 、 1,2,3,4,5,6,7
B 、 7,6,5,4,3,2,1
C 、 5,6,4,3,7,2,1
D 、 1,7,6,5,4,3,2
E 、 3,2,1,7,5,6,4

分析：这道题目不仅在微软笔试出现过，也被很多别家公司当做笔试题考过，甚至出现过相类似的算法大题。它包含一个隐藏的出栈顺序规则：对于编号较小的出现在较大的编号后面时一定是降序排列的，如：1,4,3,2 是合理的，而 1,4,2,3 就是一个错误出栈序列。这道题还需要考虑的一个问题是栈的大小是有限的，连续的降序段的长度不能大于5 。综合这两点可选出答案。

2 、 下面哪一种操作不是 stack 的基本操作？ （ 201 2年9月招聘考题）

A. 入栈

B. 出栈

C. 检查是否为空

D. 排序栈中元素

3 、以下这些序列中，哪些不可以写作一个二叉搜索树后序遍历的结果？ （ 201 3 年 9 月招聘考题）

A 、 1,2,3,4,5
B 、 3,5,1,4,2
C 、 1,2,5,4,3
D 、 5,4,3,2,1

分析：根据左右根的顺序。最后一个元素一定可以将前n-1个数分成前后两部分，一部分比它大，一部分比它小。B无法满足这种性质。

5 、 字符串与指针

1 、读程序写运行结果 （ 2011 年 4 月实习招聘考题）

[cpp] view plain copy

1. #include

2. using namespace std;

3. int func( int *s, int row, int col)

4. {

5. int count = 0;

6. int start = 1;

7. int current = start;

8. int pending = s[current];

9. do {

10. int r = current/col;

11. int c = current%col;

12. int next = c*row+r;

13. int tmp = pending;

14. pending = s[current];

15. s[current] = tmp;

17. ++count;

18. current = next;

19. } while (current != start);

20. return count;

21. }

22. void test()

23. {

24. int s[12];

25. int r = func(s,3,4);

26. cout<

27. }

28. int main()

29. {

30. test();

31. system( "pause"