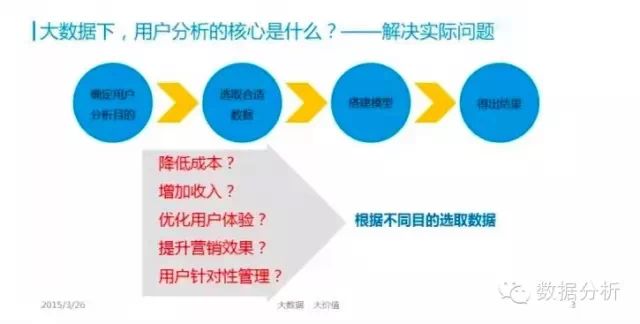
大数据下,用户分析的核心是什么? ——解决实际问题
确定用户分析目的,具体是为了降低成本?增加收入?优化用户体验?提升营销效果?用户针对性管理?
确定目的后开始选择合适的数据,然后搭建模型,最后得出结果,并用数据可视化解读。
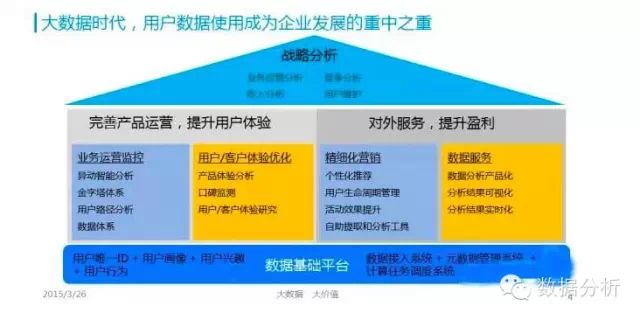
大数据时代,用户数据使用成为企业发展的重中之重。
RFM方法是国际上最成熟、最为接受的客户价值分析方法,RFM实际上是一整套分析方法中的部分内容,但最具代表性,其它还包括客户购买行为随机模型、马可夫链状态移转矩阵方法、贝氏机率推导状态移转概率方法、回归拟合方法等。 它具体的技术原理又是如何呢?

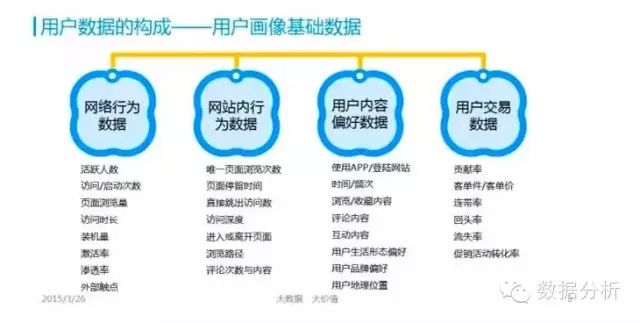
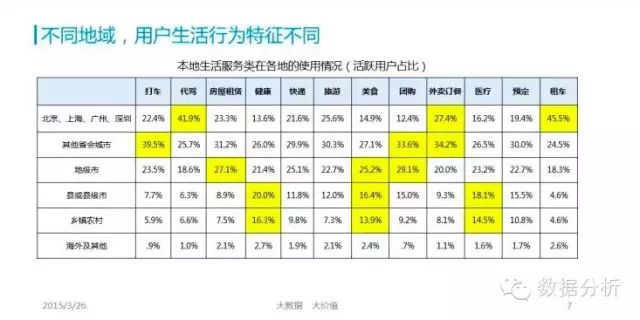
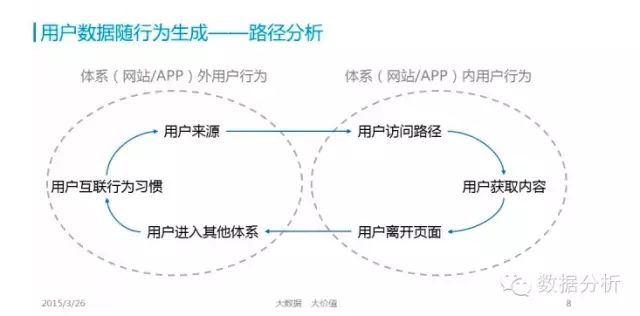
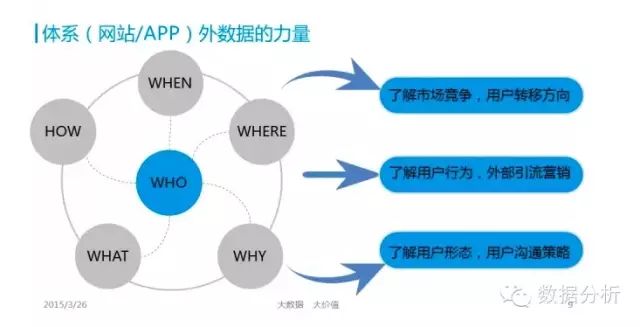

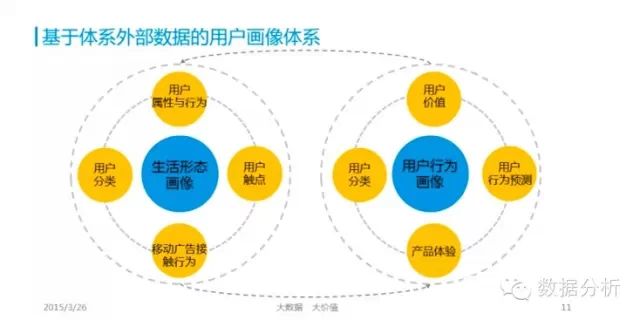
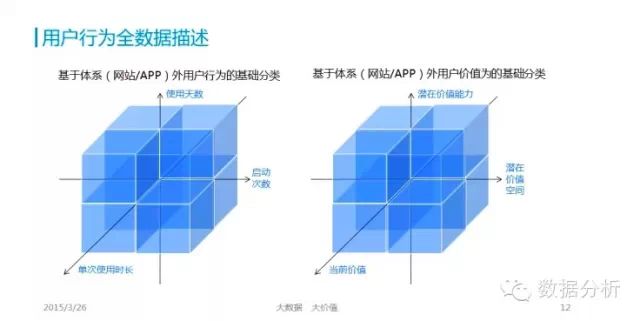
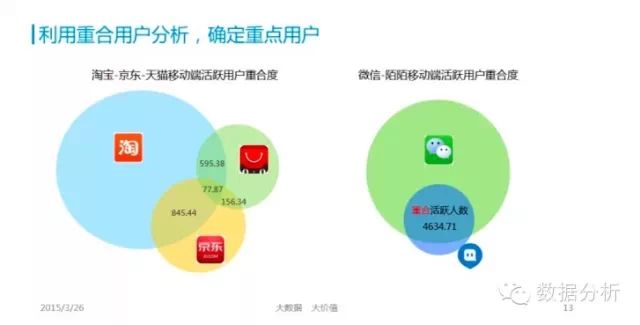
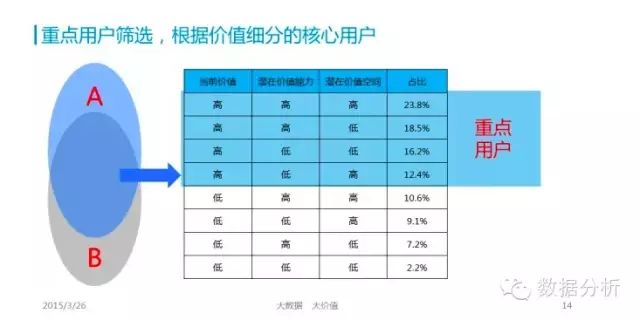
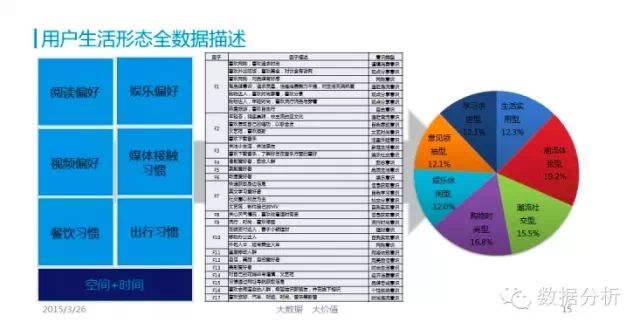

使用RFM方法(最近购买日Recency, 各期购买频率Frequency, 各期平均单次购买金额Monetary)能够科学地预测老客户(有交易客户)今后的购买金额,再对销售毛利率、关系营销费用进行推算,就能按年、按季、按月分析出今后几期的客户价值。
在这里,客户价值指CRM毛利。CRM毛利 = 购买金额 - 产品成本 - 关系营销费用。
RFM方法是国际上最成熟、最为接受的客户价值分析方法,RFM实际上是一整套分析方法中的部分内容,但最具代表性,其它还包括客户购买行为随机模型、马可夫链状态移转矩阵方法、贝氏机率推导状态移转概率方法、回归拟合方法等。
一、客户购买行为随机模型中隐藏着哪些秘密?
随机模型除了显示购买频率概率、平均金额概率的密度分配,还隐藏着购买频率、平均金额的状态移转期望值和概率这两个秘密,等待被揭示。
揭秘后,您就更加理解用必要长度和宽度的样本数据建立起一套牢固、可靠随机模型的重要意义,样本越大,客户价值推测结果就越接近即将发生的事情。
【客户随机购买行为的六个基本假设】
-
假设一:假设客户随机购买频率和随机购买金额两个不同的行为纬度互相独立,不具有相关性。
-
假设二:假设客户的购买状态移转行为符合马可夫链的假设,这表示客户下一期购买状态发生的机率只和上一期的购买状态有关。
-
假设三:假设个别客户购买频率为卜松分配(Poisson Distribution)。
-
假设四:考虑客户的异质性,假设上述个别客户单位时间平均购买次数服从伽玛分配(Gamma Distribution)。
-
假设五:假设个别客户有购买行为的各期平均单次购买金额为伽玛分配(Gamma Distribution)。
-
假设六:考虑客户的异质性,假设上述各期平均单次购买金额又符合另一个伽玛分配(Gamma Distribution)。
1、观察随机模型
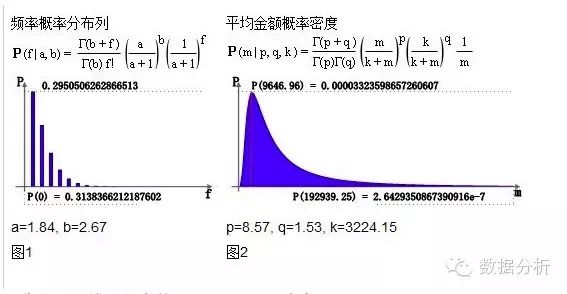
曲线形状均由其参数a、b、p、q、k决定。
频率概率分布列符合负二项分配,参数a、b由客户的平均购买频率计算出来。假设有一组样本,对应n家成交客户,fi(i = 1, 2 … n)【样本长度为n】表示每家客户的平均购买次数,通过最大概似估计法可求得a、b,并且可求得平均频率 = b/a。频率模型为离散函数,f>0,频率平均值=ceil(b/a)=ceil(2.67/1.84)=2。示例的无成交概率分布列P(0)≈31%,意味着其余有成交概率分布列之和ΣP(i)≈69%,其中P(1)≈30%(峰值),P(2)≈19%,P(3)≈10%。
平均金额概率密度符合伽玛-伽玛分配,参数p、q、k由客户的平均购买金额计算出来。假设共有n家客户【样本长度为n】,且每家客户有发生购买行为的期数分别为hk(k=1, 2 … n)【样本宽度分别为hk】,每家客户有发生购买行为期间的该期平均单次购买金额为mi,j(i=1, 2, … n, j=1, 2, … hi),通过最大概似估计法可求得p、q、k,并且可求得对应峰值概率的平均金额 = (p-1)/(q+1)*k。平均金额m的概率密度分配为连续函数,m>0,p、q为形状参数,k为尺度参数。示例的峰值概率密度位于m=9646.96,P(9646.96)=0.00003323598657260607。
从上面随机模型中您已能初步观察到购买频率、平均金额的概率分布情况。
2、推导购买频率、平均金额移转期望值
以平均金额为例,观察以下图形:
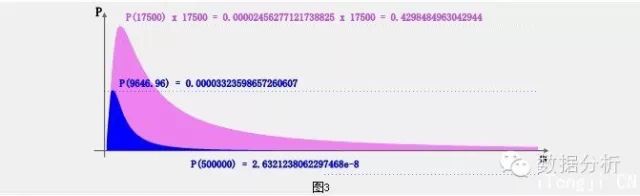
蓝色的就是平均金额概率密度曲线,紫色的是m轴每个mi坐标乘以对应蓝色概率密度pi得到的新曲线。换句话说,紫色包络线上每个点的值都是蓝色包络线对应点的mi倍。
在上图任意位置mi作条垂线,垂线至m=500,000.00(假设此为历史最大平均金额)之间,紫色面积除以蓝色面积,结果就是mi的状态移转期望值。可对m设定一些刻度,如0.01、1,000.00、10,000.00、100,000.00、200,000.00、300,000.00、400,000.00,即可得到这些刻度的对应的平均金额移转期望值。
用积分表达式描述就是:平均金额移转期望值 = ∫紫色曲线函数dm / ∫蓝色曲线函数dm,积分区间由mi到500,000.00。
购买频率移转期望值也类似,只是频率概率为离散函数。
3、推导购买频率、平均金额移转概率
从随机模型推导移转概率要复杂些,与上述求面积不同,它是一个求体积的计算(二重积分),较为抽象。
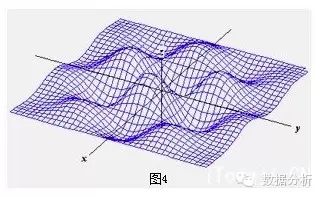
二重积分在直角坐标系中求体积的示意图如右。下面我们换个角度,不在三维坐标系中谈体积积分,而是继续用求面积这种更直观的方式来推导平均金额移转概率。
基础知识:客户从上期状态移转至下期状态,在马可夫链中记作(r1, f1, a1≤m1
|
|
平均金额由m1移转到m2的移转概率记作fm(m2 | a1≤m1
与推导移转期望值相似,当期望值m2分别等于0.01、1,000.00、10,000.00、100,000.00、200,000.00、300,000.00、400,000.00时,也可用下图的a1至b1之间的绿色面积除以对应的蓝色面积来推到平均金额的移转概率。
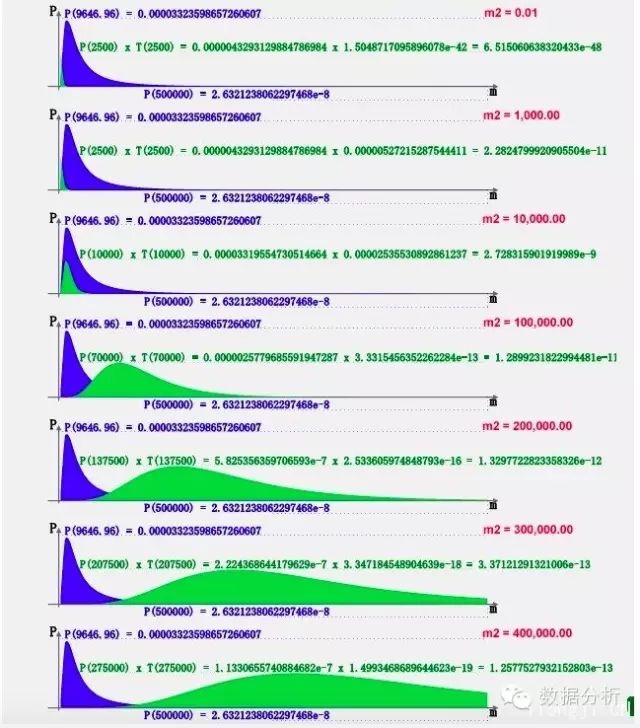
图5
图5中的蓝色曲线就是图2的平均金额概率密度函数。绿色曲线就不是平均金额概率密度pi去乘以m坐标轴的每个对应mi,而是去乘以另一个贝氏事后机率密度函数,这个函数是{[Γ(2p+q) * m2p-1 * (k+m1)p+q] / [Γ(p) * Γ(p+q) * (m2+m1+k)2p+q]},它是通过由果导因的方法获得。
当m2分别等于0.01, 1,000.00, … 400,000.00时,就得到图5的不同图形。当m2等于某值时,用m轴a1至b1之间的绿色面积除以对应的蓝色面积就得到平均金额移转概率fm(m2 | a1≤m1
用积分表达式就是:
fm(m2 | a1≤m1
其中H = ∫a1b1[Γ(2p+q) * m2p-1 * (k+m1)p+q] / [Γ(p) * Γ(p+q) * (m2+m1+k)2p+q] * [P(m1 | p,q,k)] dm1
其中L = ∫a1b1[P(m | p,q,k)] dm
而实际上m2也是一个连续变量,从a1≤m1
fm(a2≤m2
类似地,也使用贝氏机率方法推导频率移转概率,马可夫链中的r1值(无成交期数)、频率随机模型中的信任区间也是两个重要计算因素。
4、购买频率、平均金额移转期望值及移转概率计算
针对上述举例,移转期望值及移转概率的推导结果如下:
|
样本数据的最小频率=1,最大频率=3:
|
样本数据的最小平均金额=0.01,最大平均金额=499,999.00:
|
最近成交期的频率f1
下期的频率期望值f2
|
最近成交期至下期的未成交期数r1
下期的频率期望值概率p
|
|
f1≥1 → f2≥2
|
r1=0, p=0.3606;r1=1, p=0.2949
r1=2, p=0.2356;r1=3, p=0.1892
|
|
f1≥2 → f2≥2
|
r1=0, p=0.3606;r1=1, p=0.2949
r1=2, p=0.2356;r1=3, p=0.1892
|
|
f1≥3 → f2≥3
|
r1=0, p=0.1367;r1=1, p=0.0958
r1=2, p=0.0669;r1=3, p=0.0477
|
|
|
最近一期平均金额m1
|
下期平均金额的期望值m2、概率p
|
|
0.01≤m1
|
m2=39,510.75,p=0.0126
|
|
1,000.00≤m1
|
m2=39,598.21,p=0.3719
|
|
10,000.00≤m1
|
m2=46,920.90,p=0.8754
|
|
100,000.00≤m1
|
m2=186,871.69,p=0.4707
|
|
200,000.00≤m1
|
m2=296,732.74,p=0.3049
|
|
300,000.00≤m1
|
m2=379,455.72,p=0.2227
|
|
400,000.00≤m1
|
m2=445,441.60,p=0.1748
|
|
某客户下期的购买金额 = (该客户的)下期频率 * 下期平均金额 * 下期频率概率 * 下期平均金额概率
二、预测下期产品成本和关系营销费用
CRM毛利 = 购买金额 - 产品成本 - 关系营销费用。
RFM只预测客户下期的购买金额,
RFM并不预测下期的毛利率和费用。对个别客户以往的毛利率、费用采取平均法或移动平均法,应用于下期,该推断显然不合适;采取如RFM的概率分析方法去推断下期毛利率和费用也不合适,因为这两者并不是源自客户(或企业、员工)的随机行为,而更是源自企业总体成本控制和差别应对。
【销售毛利率、关系营销费用的五个基本假设】
-
假设1:假设销售毛利率和关系营销费用不是随机现象,并且毛利率、费用遵循各自的发生规律。
-
假设2:假设个别客户下期的销售毛利率最接近该客户有成交上期的毛利率。
-
假设3:假设个别客户上期、下期之间存在无交易期数,则下期销售毛利率的升、降,服从该客户在无交易期间的企业整体毛利率的拟合回归规律。
-
假设4:假设个别客户下期的关系营销费用服从该客户以往的费用、购买金额比例,即服从关系营销投入产出比。
-
假设5:假设个别客户下期可能存在一个最小关系营销费用基数,它相当于该客户以往各期费用中的最低值。
1、下期产品成本
下期产品成本 = 下期购买金额 * (1 - 下期销售毛利率)
如果某客户上、下期之间无交易期数为0,则下期毛利率 = 上期毛利率。上期指有成交的最近一期。
如果某客户上、下期之间无交易期数为r1 (r1>0),则下期毛利率 = 上期毛利率 * (1 + Δ)。其中Δ = (上期至r1=0期之间的)线性回归方程的斜率 * r1 / 2,用Δ对毛利率进行微调。之所以采用线性拟合回归,是因为决定系数R2在这里并不重要,我们仅是求得无交易期间的企业整体毛利率升、降趋势,并且不是用拟合回归方程本身去预测下期毛利率。
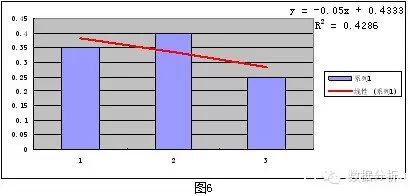
2、下期关系营销费用
定义:Ratei = Σ客户i以往费用 / Σ客户i以往购买金额
Expensei = 客户i以往各期中最小的那期费用(大于0)
Monetaryi = 客户i下期购买金额
Xi = Monetaryi * Ratei
如果Xi > Expensei,则下期费用 = Xi;
否则如果Monetaryi 否则,下期费用 = Expensei。
3、在SynleadCRM 2008中,对下期的毛利率和费用还可手工修正
用SynleadCRM 2008分析客户价值时,选项“提取产品成本”表示提取以往产品成本并推算今后几期的产品成本,选项“提取费用”表示提取以往关系营销费用并推算今后几期的关系营销费用。前面提到,产品成本和关系营销费用属于企业总体成本控制和差别应对,其未来变化不一定按趋势平滑,可能下期个别客户或整体客户群的情况出现逆反或抖动。依据您的判断,在SynleadCRM 2008中对下期的毛利率和费用还可手工个别/批量地调整、修正。
另一方面,也可能出现少许产品成本、费用数据没有及时填写进CRM系统,例如“机会-产品”中未及时填写或更新产品/销售价/成本价,造成统计时产品成本=0.00、毛利率=100%;或者极特殊的数据没有排除,例如上期毛利率为负值。该情况也需要对个别客户的下期毛利率进行手工修正。
三、完整客户关系生命周期内的客户价值
客户价值 = CRM毛利 = 购买金额 - 产品成本 - 关系营销费用。在完整客户关系生命周期内(从建立关系到未流失的最近一期),分析客户今后价值的意义远远大于分析客户历史价值,因此通常所讲的客户价值分析是对客户今后的价值进行分析。
SynleadCRM 2008为您分析客户今后三期价值的同时,也向您展示客户的历史价值作为参照。
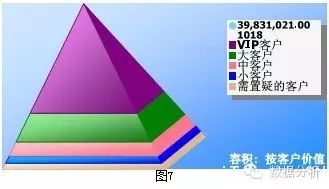
对预测出的今后客户价值结果,您就可按客户价值分层。CRM客户关系管理将传统的整体营销推进到分块差别化营销、一对一差别化营销的高度,其立足点就是客户价值差别化分析。
通过预测客户价值,您就清楚一旦VIP客户、大客户流失将在今后造成怎样的利润损失;也可以找出那些临近亏本或负价值的客户,进行置疑分析,找出对策。
也要清醒地认识到,即便预测出的客户价值较高,也只是说明其价值势能(购买潜力)较高,坐等客户送上门的价值动能(实际购买)是不现实的,必须回过头去用CRM基础方法论踏踏实实地与客户互动,推动客户追加购买、交叉购买。
客户价值分析,是企业决策最重要的依据之一,请做好您企业的客户价值分析,正确指引商务运营。
文章转自:中国统计网;ppt图片转自:杨小宝的博客;
版权声明:本号内容部分来自互联网,转载请注明原文链接和作者,如有侵权或出处有误请和我们联系。
商务合作|约稿 请加qq:
365242293
。
更多相关知识请回复:
“ 月光宝盒 ”;
数据分析
(ID :
ecshujufenxi
)互联网科技与数据圈自己的微信,也是WeMedia自媒体联盟成员之一,WeMedia联盟覆盖5000万人群。






