作者:余理华 (美国布鲁克海文国家实验室)
作为杨振宁先生的学生,我很想在这里回忆一下杨先生是怎样引导我,影响了我的思想方法,工作习惯,和研究方向的。我就从1979年我第一次见到杨先生开始。
人们可以想象我第一次见到杨先生时会有多么兴奋。我当时着迷于量子力学统计解释的问题,对于其中关于粒子波函数在测量时会在瞬间收缩到一点觉得不可思议,总想找到一种实验去检验这种说法。于是我就和杨先生讨论这个问题。正如赵午前面所讲,杨先生对学生是十分关照的。这个问题杨先生很耐心地和我谈了两次。第三次时,杨先生说:我想过了。这个问题的确很神秘。但今后我不能再跟你谈这个问题了。这是一种obsession。如果有了obsession,是可以一事无成的。这无疑对我是一次非常重要的影响。我终于明白了,打断了这种痴迷。
后来在多次与杨先生的交谈中杨先生常讲到他的一个习惯:如果他想一个问题,有两三天没有进展,他就会把问题放下,去考虑一个新的问题。这也影响了我后来的习惯。如果我考虑一个问题,很久没有进展,又舍不得放下,我便想到了杨先生的话,将问题暂时放下了。

图1 1993年杨振宁先生帮我修改文章
又一次,在聊天中,杨先生问我怎样读书。我说我一行一行地读。如果有一行不懂,我就反复读,查阅和推导,直到我懂了。杨先生说,这并不一定是唯一的读法。另一种读法是“跳着读”,一下跳过好多页,甚至几章以后,然后再跳回来。他的一个儿子就是这样读书的。我立即觉得有道理。后来我也常常这样。因为不是每一本书都需要细读的。如果都细读,所学的就会太少了。
在石溪,有一次学术报告我听不懂,感到十分挫折。中间休息时,我见到杨先生就问他怎么这么难懂?他说这很常见,常常有许多是听不懂的,没关系,但需要像伸得很高的天线一样,能抓住一点信号,尽管听不懂,往往还是能找到新的问题的。这样我就不再那么害怕听不懂了,往往还会学会一点新东西来解决其他的看似无关的别的问题。
在杨先生六十寿辰时,石溪同学会请杨先生讲话。其中他说到研究生时期是人生最困难的一个时期。我听了觉得受到了很大的鼓舞。这是因为研究生作问题不再像以前那样只做老师出的题目,而需要寻找一个能做出来而且又有意义的题目,当时我正困惑于此。听到杨先生这段话我感到很大的安慰。既然如此,我的困难也就是一般情况了,也会被克服的。
杨先生又讲到,对一个问题而言,知道有答案是一个很重要的启示。为什么我们在考试时往往能做出十分困难的问题?因为我们知道考试题一般是有答案的,我们会尽全力去寻找答案。我想这一点表面上似乎很简单,实际上关系到研究领域的中心问题,就是要判断一个问题有答案的机会是否较大。我们要选有希望的方向走,才会有更大的机会成功。
跟这一点直接相关的,杨先生常常说到的,就是要寻找新的方向。如果某一个矿藏是一座老的矿藏,许多人在那里发掘过了,你在那里就很难发现新的东西。如果有一个新的矿藏,那你一旦进入那里,有时就会发现遍地都是宝。因此寻找新的方向是十分重要的。
我这里所谈到的,只是我从杨先生的教诲中领会到的许多观点中的一小部分。可以看到,这许多道理常常看起来是非常明显的, 杨先生一说到,我就会觉得当然是对的。但另一方面,杨先生没说之前,有许多我却没有注意到。而且仔细想来,这里面又有很深的道理,这些对我的思想方法有深远的影响。
正如前所说,那个时期我就在寻找新的方向。也正如赵午所说,杨先生常常说起高能物理的现状。杨先生说高能物理的发展依赖于大型加速器的发展。现在的高能加速器越造越大,越来越贵,这种趋势难以长期持续下去。这会导致高能物理缺乏大量新的实验数据,高能理论的发展就会出现“粥少僧多”的情况。就是说,研究高能理论的人太多,而可做的题目,在缺少大量数据时,却越来越少。
这样就促使我在更大的范围内寻找新的方向。也就在这个时期我听到了来自布鲁克海文国家实验室的一项关于自由电子激光的报告。这是一个全新的方向。在这样的情况下,经过考虑,我终于决定离开我所爱好的粒子物理方向,在1981年末作为石溪的研究生来到布鲁克海文国家实验室,转向了自由电子激光,1984年取得了博士学位。
正如杨先生所言,自由电子激光这个新的发展方向充满了新的课题。在我加入这个方向的时候,正在出现一个新的概念,即高增益自由电子激光。在高增益条件下,电子束可以将很弱的输入光在一次性穿过扭摆磁铁后指数放大到很高的强度。由于不需要镜面,这种方法有可能适用于缺乏反射镜面的短波激光。于是出现了X 射线激光的可能性。
在1987—1988 年间,世界范围内的高增益自由电子激光已经发展到我们对其有许多定性的了解。但我们仍然不知道什么样的参数可以导致X射线激光的实现。为了寻找实现X射线激光的条件,我们需要定量的方法能在短时间内扫描大量的参数空间来优化各种参数。在1989 年我和SamKrinsky 终于推导出了定量计算高增益的公式,发表在《物理评论快报》上。经过优化我们得到了一组X 射线激光的参数。这些参数表明当时的技术已接近可能达到软X 射线,距离硬X射线还差大约10倍。
那时我仍常常见到杨先生。在与杨先生谈论中,他认为技术的改进往往是非常快的,也许几年就可以改进几倍甚至几十倍。这样看来硬X射线激光是可能的。我与Sam 讨论后决定与我们的副所长R. Palmer 谈一谈这项进展。我俩在他的办公室黑板上列出那组数据。看到这组激动人心的数据,他决定召开一个专题讨论会, 叫做“ Prospects for a 1 Å Free-Electron_Laser Workshop”, 即“1 埃自由电子激光展望研讨会”。这样,X射线激光便不再只是一种可能或希望,而是有了具体可行的方向和指标。
这个研讨会于1990 年4 月在布鲁克海文附近的Sag Harbor 召开。会上我在题为“Scaling Relations and Parameters for 1 Å FEL”的报告中第一次给出了1 Å 自由电子激光的具体数字(图2)。19 年以后建成的世界上第一个X 射线自由电子激光(LinacCoherent Light Source,LCLS)设计的波长是1.5 Å,仔细对照图2
表中最后一列参数可以发现,因为这组数据用的是1 Å而不是1.5 Å,这与多年后LCLS 的设计数据大约只差不到一倍。该组数据显然适用于直线加速器提供的电子束。
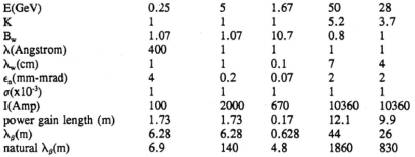
图2 右列为1 Å自由电子激光的具体数字(摘自“Prospects for a 1 Å Free-Electron_LaserWorkshop”)
两年后,即1992 年,Barletta, Sessler和我发表了一篇题为Using the Two Mile Accelerator For Powering An FEL的文章,再次给出了用SLAC的直线加速器建造1 Å和40 Å自由电子激光的两组参数。该文与Pellegrini同时发表的一篇建议用SLAC 的直线加速器建造X 射线激光的文章为发起LCLS 奠定了理论基础。图3 的示意图表达了这些工作与LCLS 之间的逻辑关系。我们知道,LCLS于2009年开始运行。

图3 两次研讨会与LCLS之间的逻辑关系
这些理论都是关于自发辐射放大的。这种辐射频带宽,不完全相干。为此我发展了“高增益谐波发生”(High Gain Harmonic Generation) 的过程来产生全相干光,简称HGHG。自1990年后我们便致力于用实验来验证这些理论。1997 年及2002 年我和Sam 与Ilan Ben-Zvi 及其他小组成员在布鲁克海文国家实验室分别实现了5 μm和266 nm的HGHG实验,分别发表在Science 和《物理评论快报》(图4)。这些实验不仅证实了我们关于增益的计算, 也证实了关于自发辐射启动功率和谐波发生启动功率的理论。至此,关于X 射线自由电子激光的参数已经确信无疑了。
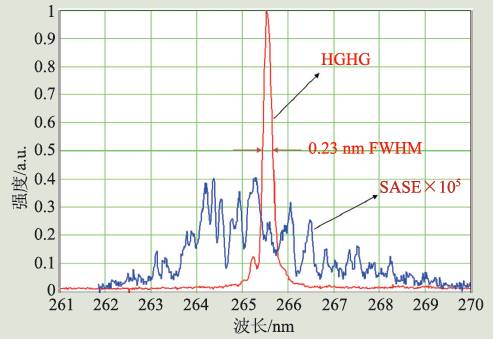
图4 2002 年HGHG光谱与自放大的自发辐射光谱的比较(摘自PRL,91,7,074801 (2003))
自从到布鲁克海文国家实验室后,我有幸继续常常见到杨先生,谈起各方面的有趣题目。1997年前后,在交谈中杨先生问起我X射线自由电子激光的进展情况,我表示我认为这是一定会成功的。杨先生说,“既然一定会成功,我应当建议中国发展自由电子激光。”杨先生很快开始了行动,向中国科学界的领导人建议向X 射线自由电子激光方向发展。杨先生建议由陈佳洱、陈森玉和我在国内组织发展高增益自由电子激光。之后他又多次写信,关注事情进展。
从此以后,我曾多次回到北京和上海,协助中国科学院高能物理研究所、北京大学、中国科学院上海应用物理研究所发展高增益自由电子激光。在前面的报告中,陈佳洱先生更为详细地介绍了这些发展,而且展示了当年杨先生的建议书。陈佳洱先生还介绍了上海应用物理所取得的成功,我们看到了上海应用物理所相关谐波发生的实验结果在Nature 杂志上发表的文章。我在这里想提到的是另一项重大成果,即大连相干光源的成功。中国科学院大连化学物理研究所在上海应用物理研究所的协助下于2017 年1 月建成了工作在20—100 nm 范围内的相干自由电子激光,所用的原理是HGHG。这个激光是世界上第一座该波长范围内的自由电子激光。其强大的全相干的激光吸引了世界其他国家的科学家来大连做实验。这项成功取得了世界科学界的承认,并于2017 年1 月20日在Science上报道了。
中国科学院上海应用物理研究所正在试行运转一项软X射线自由电子激光,而且正在发展一项更大规模的高重复频率的超导加速器驱动的硬X射线自由电子激光。中国的自由电子激光事业在杨先生的推动下已经向前迈出了一大步。
当我在布鲁克海文进行自由电子激光和其他存储环相关的工作时,我有幸继续与杨先生常常讨论各种物理问题。
1993 年前后,量子力学的基础问题中出现了进展,叫做“去相关性”。杨先生知道我一直关心着量子力学统计解释的问题,特别是波函数在测量时的突然收缩。他找了我和当时正在石溪访问的孙昌璞讨论去相关问题。经过一番努力,我们解开了一个遵守薛定谔方程的粒子与一个充满了简谐振子的环境相互作用的问题。答案表明,波函数会收缩,而收缩时间等于粒子振动的衰减时间。而且波函数会收缩成一个由互不相干的点函数组成的统计分布。我们发表的文章显示了波函数收缩成点函数的过程。这显然是一个十分有趣的答案。由此刚到石溪时我心中抹不去的那个波函数收缩问题,虽然关于收缩到分布函数中的哪一点的问题仍然似乎神秘莫测,但毕竟从完全不可思议变得清晰了许多。使我得到了人生认知上的一个完全出乎预料的大收获,这是人生最大的快乐之一。特别是,当想到我在此文开始时提到的怎样打破我刚到石溪时的obsession,我更加感激杨先生的指点。
1995 年前后,物理学上出现了一项重大的突破,就是玻色—爱因斯坦凝聚在气体中的实验证实。杨先生在20 世纪50 年代曾在此方向上做过非常重要的理论工作。40 年前的理论工作终于可以与实验比较了。新的实验情况与40 年前理论中的实验环境有所差别,这在于新实验中的粒子有一个位井。为了能比较,需要加上位井。为了能推导公式,这次我对杨先生的文章必须一行一行地读。在我了解了杨先生的这个理论后,杨先生在讨论中提出了一个十分具体的问题,即能否求出在粒子相互作用为零时分布函数的精确解。经过考虑,我想到如果按照费曼一本关于统计物理学的课程书中所讲,把现在问题中的温度换成虚数的时间的倒数,这个问题的解就变成前面所提到的波函数收缩问题的解。这样两个看似毫不相关的问题居然是有密切联系的,体现了物理学理论之美。杨先生采纳了这个解,作为后来在物理评论中发表的一篇文章的一小部分。我从中再次感到与杨先生工作中得到的巨大快乐。
最近,我在存储环的工作中找到了一种用方阵解开非线性方程的方法。想到杨先生所讲到的关于新矿藏有时可能会遍地是宝,这方法又是新的,我又有了更大的动力去寻找更新的解法。杨先生是我前进的动力。
祝杨先生95寿辰健康!快乐!















