本文经AI新媒体量子位（公众号ID:qbitai ）授权转载，转载请联系出处。

本文共 4200 字 ，建议阅读 12 分钟 。

“有时候，正是那些意想不到之人，成就了无人能成之事。”—— 艾伦·图灵

106年前的6月23日，阿兰·麦席森·图灵在英国伦敦出生。

1968年，也就是图灵逝世14年后，一份此前从未发表过的图灵论文原稿出现在了《科学美国人》杂志上。

在这篇写于1948年、题为《智能机器》的论文里，图灵第一次为世人勾勒出了人工智能领域的轮廓。

本公众号对话界面回复 “图灵” ，即可下载图灵1948年《智能机器》论文。

他不仅为联结主义理论奠定了基础，还引入了多种对于日后的AI研究至关重要的概念。

而在此之前，联结主义被广泛认为起源于1957年首次发表相关论文的弗兰克·罗森布拉特。

然而，图灵这篇跨时代的论文在当时被自己的领导、英国国家物理实验室主任查尔斯·达尔文斥为“小学生作文”，不予发表。

一份伟大的思想，就此失去了提早照亮世界的机会。

观其一生，图灵对于宣扬自己的思想始终缺乏足够的热情。他古怪、孤僻、木讷，任凭自己和作品在偏见中被埋没，并最终如愿以偿……

如同那份被埋藏的论文手稿——阿兰·图灵，最终成为了被遗忘的那个人。

算出不可计算之物

1935年，图灵23岁。

这一年，他构想出了一种后来被世人称为 “通用图灵机” 的抽象设备。这种设备拥有无限的内存，能够同时存储程序和数据；它还包括一个在内存上以一个符号为单位前后移动的扫描器，用于读取信息及写入额外的符号。

机器的每一种基本行为都十分简单，比如“识别扫描器所处位置的符号”，“写入‘1’”或是“向左移动一个位置”。但当大量类似的基本行为联结在一起，结果就会变得复杂。

虽然结构简单，但一台通用图灵机足以执行今天最强大的计算机能够完成的任何任务——事实上，所有现代数字计算机本质上都是通用图灵机。

在1935年，图灵的目标是设计出一台尽可能简单的机器，让它能在无限的时间、功耗、纸和笔以及完美的专注度下进行任何人类数学家能够借助算法完成的计算。称其“通用”，就是因为它有能力进行所有类似的运算。

图灵本人曾写过：“电子计算机是为了执行任意特定的、依靠经验法则的处理进程，这些进程原本可以由人类以一种有规则但却笨拙的方式完成。”

理论而言，图灵成功了。不过，一个引人注目的问题依然随之产生：我们有可能设计出甚至比通用图灵机更加强大的机器吗？

有段时间，超计算（Hypercomputation）领域吸引着越来越多的科学家。一部分人猜测，已知最为复杂的信息处理器——人脑本身——就是一个超计算机（Hypercomputer）的自然实例。

而在人们真正燃起对于超计算的兴趣之前，所有已知对于通用图灵机而言过于复杂的信息处理工作都被作为“不可计算之物”而忽略。从这个意义上讲，一台超机器（Hypermachine）应该能够算出 “不可计算之物” 。

“不可计算之物”的实例在数学领域十分常见。比如，对于一些随机选定的算术陈述，一台通用图灵机并不能判断出哪些属于定理（如“7+5=12”）以及哪些不是定理（如“任意一个数都是两个偶数之和”）。

还 有一种“不可计算的”问题来自于几何领域。 一组大小不同、各条边的颜色也不同的正方形瓷砖是否能“铺满“一个欧几里得平面（没有空隙、没有重叠且接合各边的颜色相同视为“铺满”）？夏威夷大学的逻辑学家William Hanf和Dale Myers就曾发现过一组通用图灵机无法计算的瓷砖。

在计算机科学领域，一台通用图灵机无法一直预测对眼前的程序是会终止，还是会永远继续运行下去。有时这种情况被人们称为，没有通用目的语言（Pascal、BASIC、Prolog、C等等）能够拥有一个哪怕最简单的崩溃调试器，它们难以发现能够导致崩溃的故障，包括那些会引发无限处理循环的错误。

图灵本人成为了第一个对所谓“超计算机”的构想进行研究的人。 1938年，在自己的博士学位论文中，图灵描绘了“一种全新的机器”——“预言机”（O-machine）。

““预言机”“即一台通用图灵机加上一个黑箱后得到的成果。黑箱又被称为“预言家”（Oracle），是一种用以执行那些“不可计算的”任务的机制。

而在其他方面，”“预言机”“都与一般的计算机十分相似。输入一个被数字化编码过的程序之后，”“预言机”“会通过重复的基本行为组合一步步地输出结果。其中一步就是向“预言家”传输数据并记录其反馈。

图灵并没有说明“预言家”是如何工作的（他也从没解释过通用图灵机的那些基本行为——识别扫描器中的符号”是如何实现的）。不过单从概念上看，一种能够满足“预言家”特性的机制并非难以想象。

原则上，如果神经元的活动被去同步化，一个合适的B型网络就能对那些“不可计算之物”进行计算（如果存在一个能让各神经元协调工作的中枢生物钟，该网络的运作就能在一台通用图灵机中被精确地模拟出来）。

在超计算理论中，像“分辨算术定理和非算术定理”这类任务都不可解；即便是能够分辨出程序是否由C语言写成的调解器，也会陷入理论上可能的无限循环。

而如果超计算机能被制造出来，那么用它破解那些看似不可解的逻辑和数学问题的潜力将会十分巨大——不过，相关的研究尝试也很可能因无法满足实现“预言家”所需的条件而告吹。

在数理逻辑之外，图灵的”“预言机”“几乎被忘得一干二净；相反，一个神话被人们供奉了起来：在一份子虚乌有的记录中，图灵在二十世纪三十年代中期成功证明了超机器是可能的——传言中，他与自己在普林斯顿大学的博士生导师阿隆佐·邱奇宣称一台通用图灵机可以精确地模拟任何其他信息处理机器的行为。

这条被广为误读的 “邱奇—图灵论题” 意味着，没有机器能够解决通用图灵机能力范围之外的任务。

但事实上，邱奇和图灵只说过，一台通用图灵机能够模拟任何人类数学家在使用笔和纸的情况下借助算法完成的工作——对于一个神话而言，这个命题显然过于薄弱了。

图灵对于超计算机的理论贡献无疑被忽视了——即便是对于工作于这一领域的研究者而言。专家们永远谈论的是要执行“超越图灵局限”的信息处理任务，称自己的工作是在尝试“打破图灵障碍”。

《新科学家》杂志上曾有一篇报道甚至声称，全新的机器已经“超出了图灵的概念范畴”，它们是“图灵从未构想到的计算机类型”……

就仿佛半个世纪前，那位来自英国的天才从未踏足过这片领土。忧伤的是，那只不过是图灵联结主义思想的又一次复活罢了。

图灵联结

数字计算机都是无与伦比的神算子。如果让它们预测火箭的发射轨迹，或是计算大型跨国公司的账目，它们可以在几秒内就给出答案。

然而，换成那些对于人类而言轻而易举的事情——比如认脸或是阅读手写的文字，机器会变得完全不知道从何入手。

也许是因为组成人脑的神经元网络具备专门应对这类任务的部门，而普通计算机没有。因而，科学家们开始尝试开发结构更加接近人脑的计算机。

1948年，图灵36岁。

这一年，他在一篇未能发表的论文中第一次引入了 联结主义 的思想。在论文中，图灵发明了一种他称之为“B型非结构化机器”的神经网络，包含人工神经元以及可以对神经元之间的联结进行调节的设备。

B型机器中的神经元可以是任意数量，也可以以任意模式相联结，但依然神经元之间的联结必须通过调节器。

所有调节器都具有两条训练光纤。 向其中一条光纤上加置一个脉冲，会将调节器设定为“通过模式”：在这种模式下，一个输入（0或1）将会原封不动地从中通过并转化为输出。

而在另外一条光线上加置的脉冲将会把调节器设定为“干预模式”：在这种模式下，无论输入为何，输出结果都将为1。在这种状态下，调节器会将所有试图通过的信息全部破坏。

一旦被设定完成，调节器将会一直保持“通过”或“干预”的状态，除非其收到另一条训练光纤上的脉冲。这一独创性的设计使得B型非结构化机器能够以图灵称之为“适度干预，摹拟教育”的方式来进行训练。

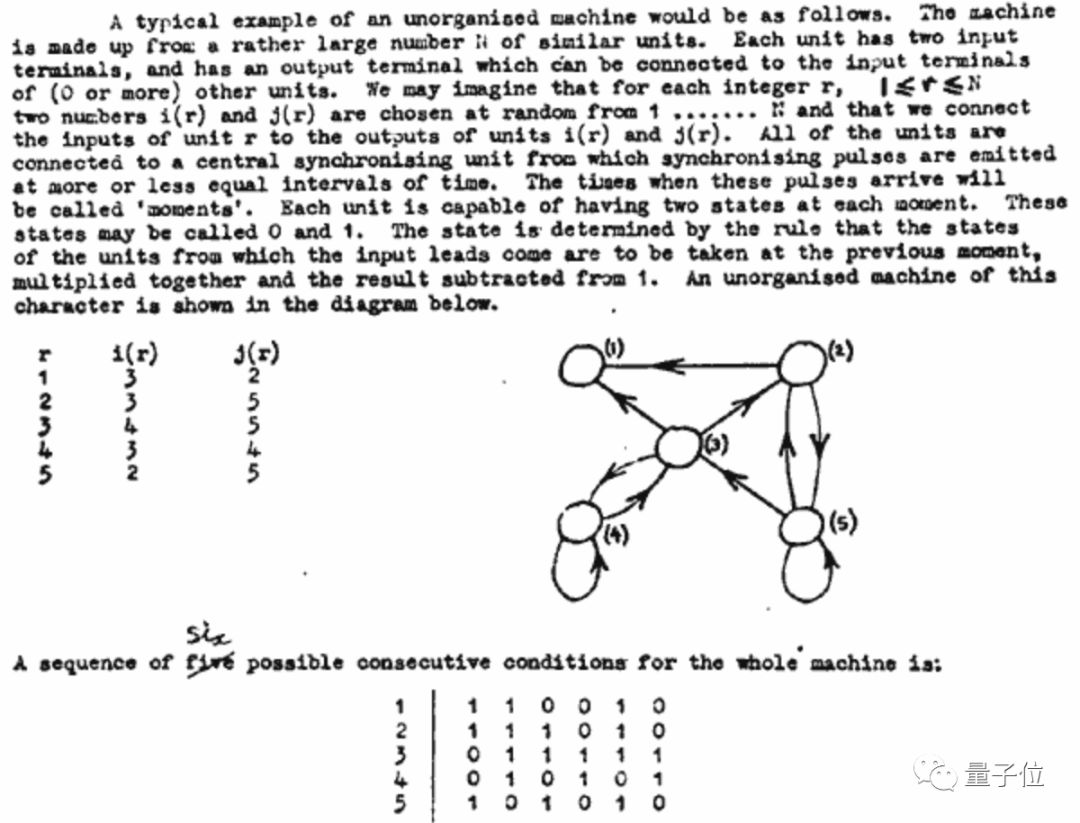
事实上，正是图灵创立了“幼儿的皮层是一个非结构化机器，可以通过适度干预训练来实现结构化”的理论。

图灵设计的每个神经元模型都有两条输入光纤，而每个神经元的输出就是两个输入的逻辑函数。网络内的每个神经元都执行相同的逻辑操作——“与非”（NAND），即只要其中一个输入为0，则输出为1；如果两个输入均为1，则输出为0。

图灵选择“与非”是因为所有其他的（布尔）逻辑操作都可以通过与非神经元的组合实现。 更进一步，图灵还证明了连联结调节器本身也能通过“与非”来构建。 因而，图灵指定了一种只由与非神经元和它们的联结光纤所构成的网络——这也几乎是最简单的大脑皮层模型。