一个简单的行星运动轨迹，是如何引导我们去探索空间和时间的

中科院物理所 · 公众号 · 物理 · 2017-04-01 10:59

正文

用一根弦将两点相连，会得到一条直线。从弦的一端以另一端为圆心走一圈，就会得到一个圆。一条直线和一个圆，两种如此简单常见的形状，构成了几何里最基础的形状。

早期的天文学专注于标注时间，比如什么时候冉冉升起的太阳会出现在最北端，或者新月再次出现的天数。而这些简单的曲线几何给了我们机会将地球与天空联系起来。月亮、太阳甚至是其它的恒星看起来就像是绕着地球做圆周运动。同样地，一个下落的球会笔直的砸向地面，燃烧的火焰成线性的上升。圆和线就像是天地间神圣的几何形状。

△ 《几何原本》。（图片来源：Biography Online）

大约公元前300年，欧几里得写下了一部不朽之作《几何原本》（共13卷），建立了空间秩序最久远最权威的逻辑推演语系。他从五条关于线和圆的基本假设（公理）开始：

任意两个点可以通过一条直线连接。
任意线段能无限延长成一条直线。
给定任意线段，可以以其一个端点作为圆心，该线段作为半径作一个圆。
所有的直角都全等。
同平面内一条直线和另外两条线相交，若在直线同侧的两个内角之和小于180度，则这两条直线无限延长后在这一侧一定相交。

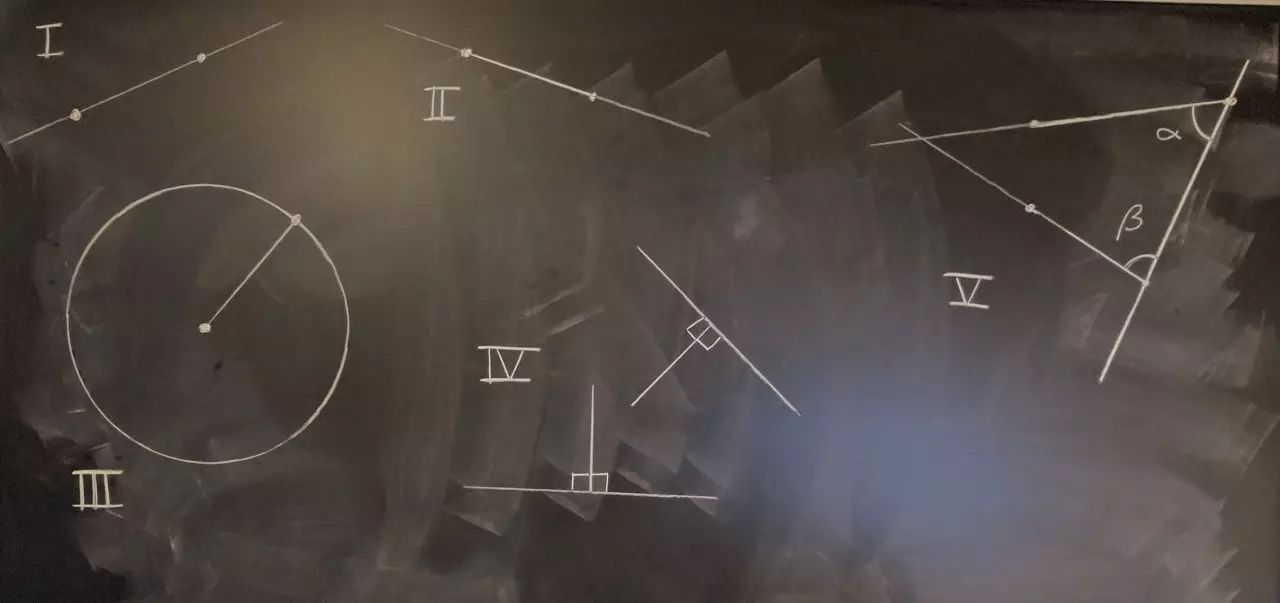
△ 欧几里得的五条公理。（图片来源：One Universe at a Time）

从这些公理，他发展了一套证明的方法和定理，如果这些最初的公理是正确的，那么几何的其它方面都必须是正确的。欧几里得赋予了我们几何的语言，才有了今天现代数学的语言。这些几何语言可以被用来描述天体的运动。如果你想知道火星和木星什么时候离我们最近，或者金星什么时候看起来像一颗晨星，你就需要利用几何来计算。

利用这些简单的几何，人们可以计算出那些天体绕着地球的真正轨道。但是，很快人们就意识到行星绕地球的运动并不是圆形轨道。在过去，线和圆在解决问题上是如此的有效，以至于大多数人提出来的解决方法还是专注在它们身上，比如，行星其实是绕着太阳做圆周运动或者本轮和均轮的概念。虽然提出来的诸多模型都比先前的更为复杂，但都不能解释真正的问题。

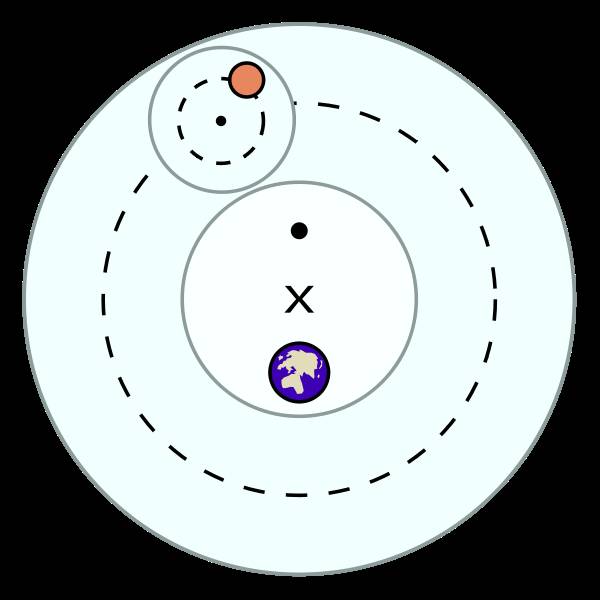
△ 一颗行星在本轮（小的虚线圆）和均轮（大的虚线圆）上。（图片来源：Wikipedia）

最终的答案来自于开普勒，他认为行星是绕着太阳进行椭圆运动，而不是圆形。

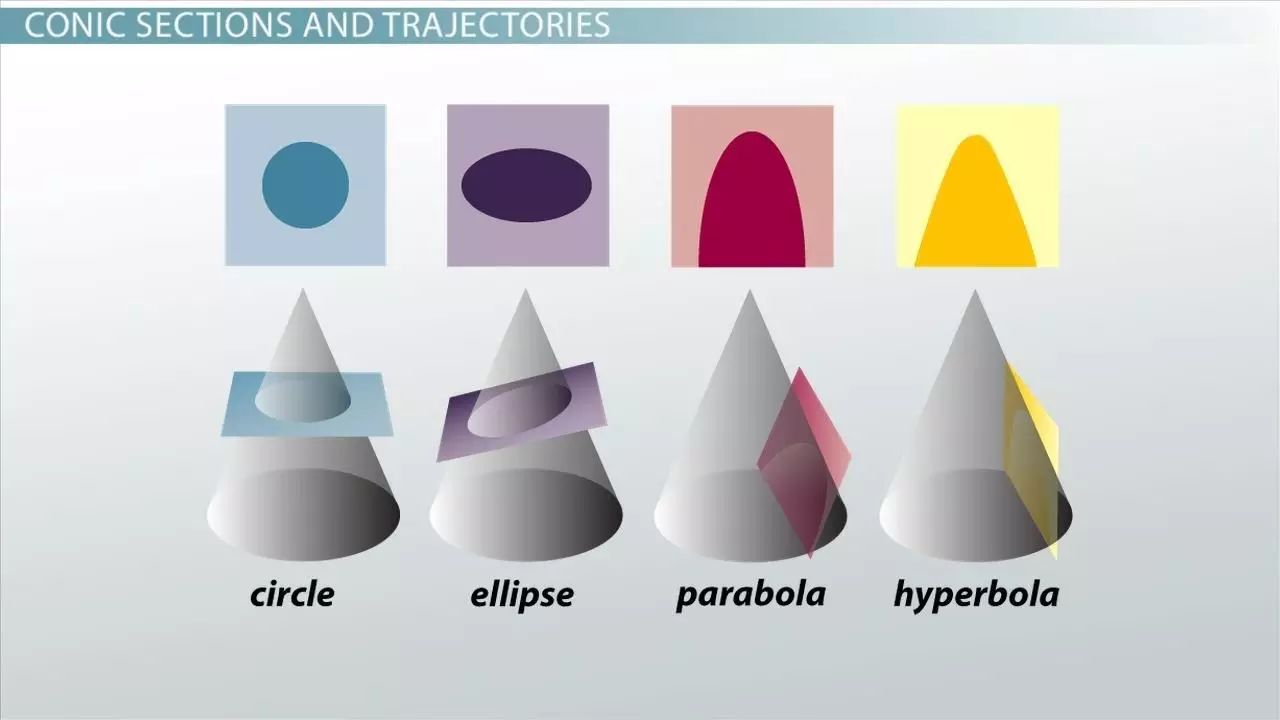
△ 四种圆锥曲线。（图片来源：One Universe at a Time）

椭圆是属于圆锥曲线的一员，通过从不同的角度平切圆锥可以得到四种类型的的曲线：圆、椭圆、抛物线和双曲线。从圆到椭圆的扩展，开普勒发现了行星运动的三个基本定律，被称之为开普勒定律。这些定律不仅能够准确地描述行星的运动，而且相比其它的模型更为简单。

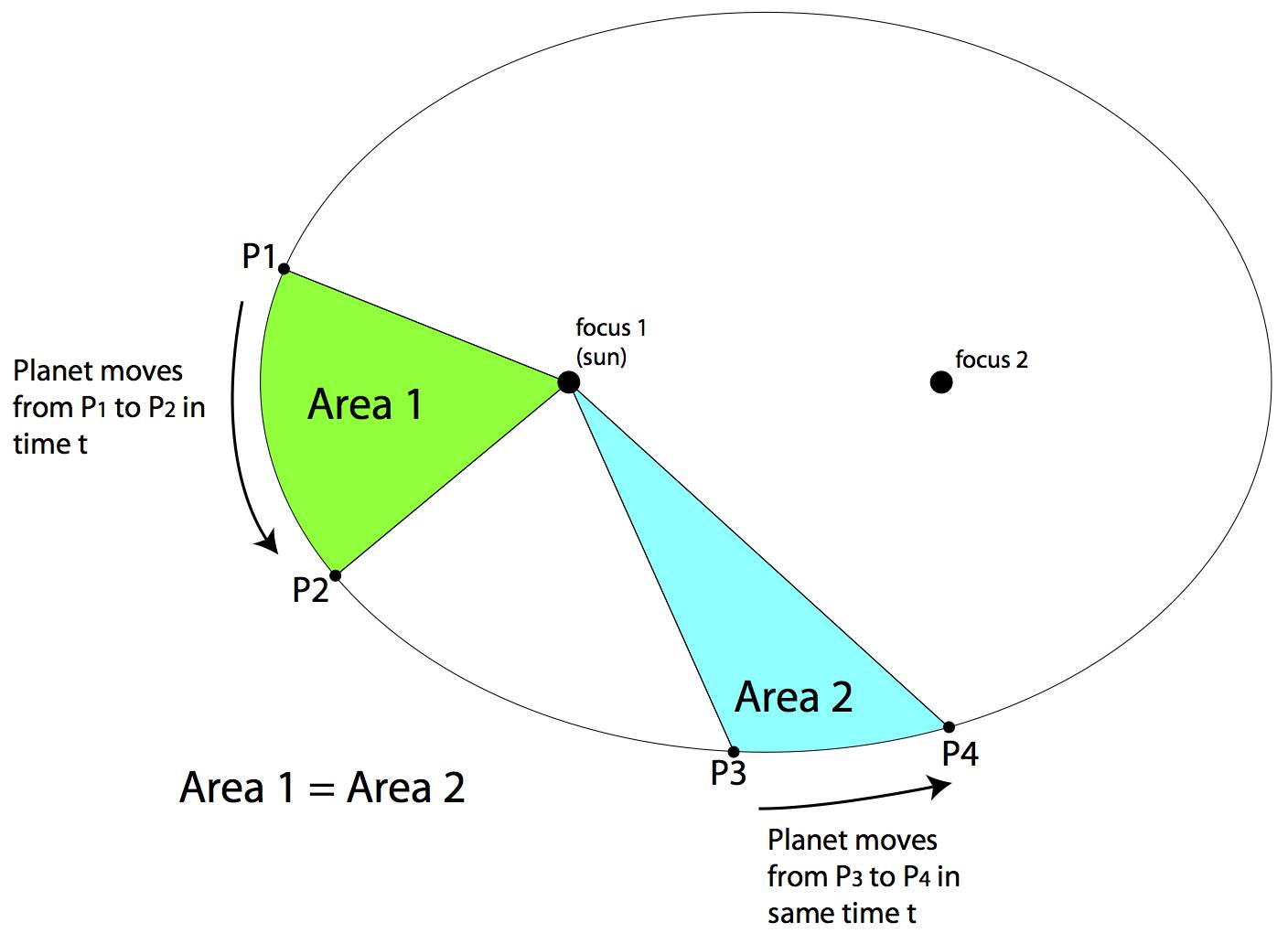
△ 开普勒第二定律：相同时间内，行星扫过的面积相等。（图片来源：One Universe at a Time）

大约在同时期，笛卡尔发展了一种描述几何的新方法。尽管在过去我们对几何图形的理解有飞跃的进步，但都依赖于欧几里得的方法。想象一条线平分一个圆，一个圆嵌入在一个立方体之中。几何都是关于线、曲线和不同形状之间的联系，而这往往很复杂。举个例子，开普勒的第二定律用一条线连接行星和太阳，在相同的时间内，这条线扫过的面积相等。

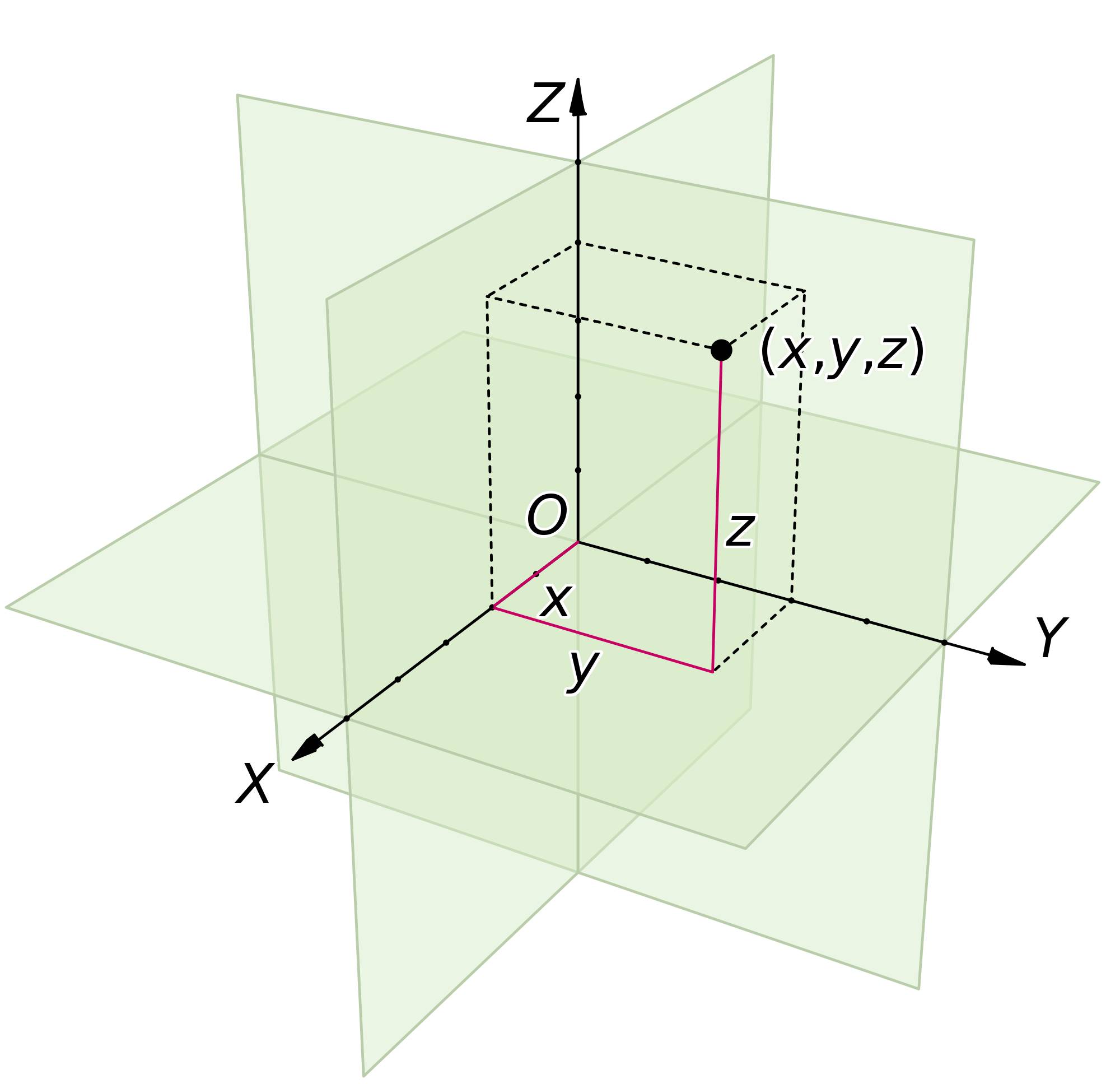
△ 空间的每一点都有独一无二的坐标。（图片来源：One Universe at a Time）

而笛卡尔把空间想象成充满了网格作为参考系。如此，空间中的每一个点都可以用独一无二的一套数字（坐标）来表示，一条曲线可以代表一个函数，连接不同的坐标。有了这种解析几何，笛卡尔将几何和代数联系在一起，给了我们更多的工具描述曲线和形状。

解析几何不仅把运动看做是经过空间的路径，也把它看成是经过时间的路径。在空间中的每一点都可以用三个坐标数字来表示它的位置，通过加入第四个表示时间的坐标，我们就建立了在哪里和什么时候的几何。当牛顿发展他的运动定律的时候，他用速度和加速度来描述运动。利用解析几何，他可以连接那些时间的函数和空间中的曲线，从而计算出物体在空间和时间中的路径。这个方法也被牛顿用来证明开普勒的运动定律其实是万有引力的结果。

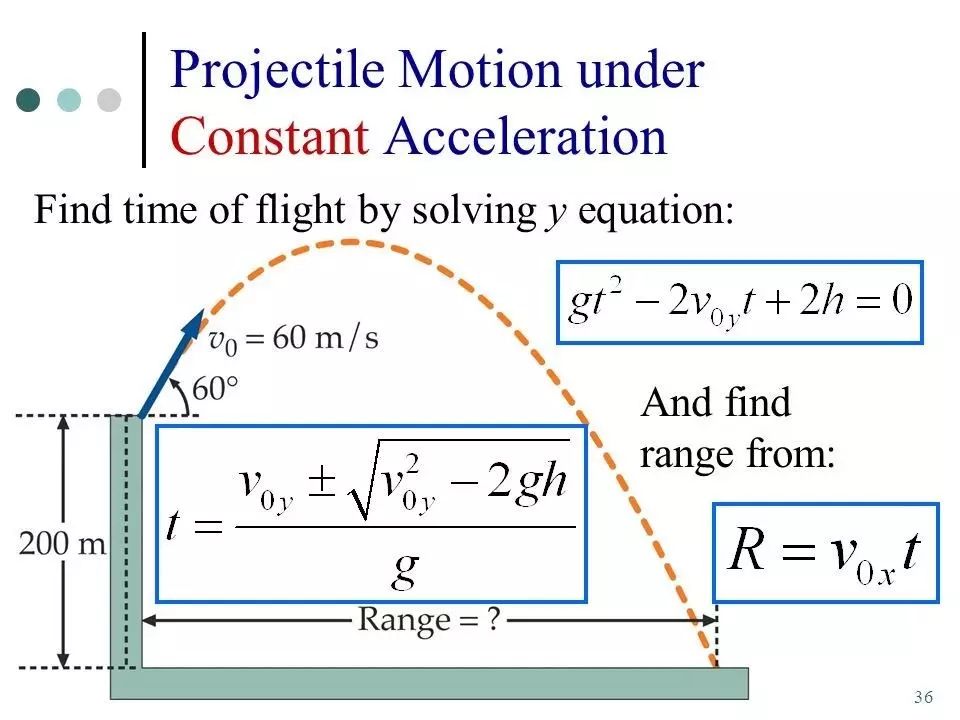
△ 牛顿的空间和时间几何在今天仍然在使用。（图片来源：One Universe at a Time）

欧几里得几何是如此的强有力，它的有效性似乎不容置疑。结合牛顿力学在当时的地位，我们似乎已经达到了理解的一个顶峰。

但是，在19世纪，一个年轻的数学开始探索欧几里得几何的替代，他就是黎曼。笛卡尔坐标系可以用来描述欧几里得的几何空间，但如果这些坐标之间的联系可以被扭曲呢？我们可以把欧几里得表面想象成一张画满了网格的纸。但如果这张纸其实是由橡胶做成的，拉伸或扭曲这张纸就可以破坏格子的形状。有一些几何规则仍然可以应用在这张纸上，但欧几里得的五个基本定理可不一定。就像圆是圆锥曲线的一个例子，欧几里得几何只是一个更大的几何家族中的一员。

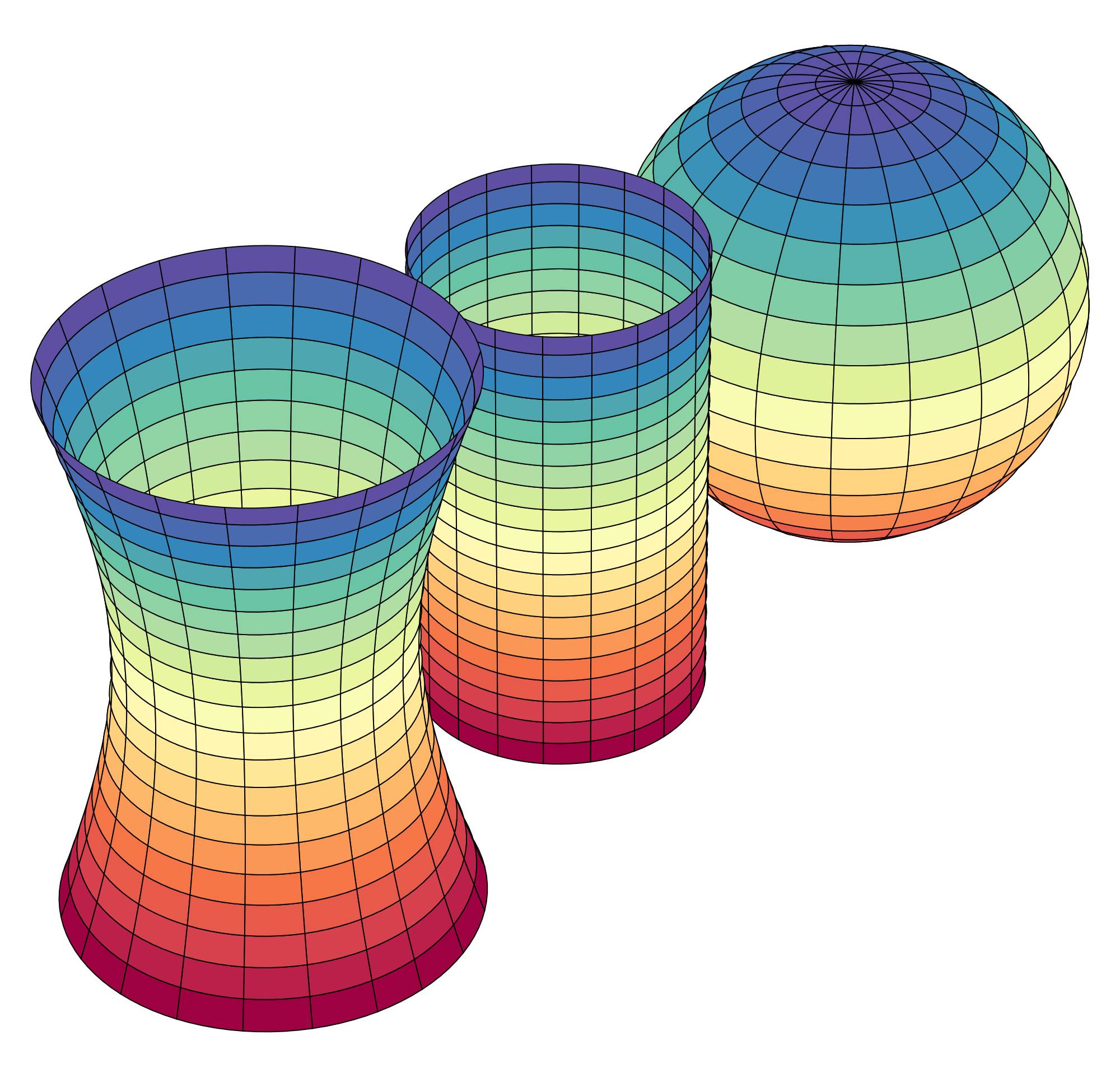
△ 黎曼几何有许多不同的形状。（图片来源：One Universe at a Time）

黎曼开启了几何的一个新篇章。在黎曼几何中，空间不再是固定的背景，而是可延展的流形。在空间中的点之间的联系由流形的结构所决定。欧几里得的规则显露了它的局限性。平行的两条线可能会相交，三角形的内角和不再是180度，两个周长一样的圆可能有不同的半径。就像笛卡尔将几何和代数联系在一起，黎曼将几何和拓扑联系了起来。几何不再限制于固定的背景网格。

但是，黎曼几何对于我们理解宇宙有什么影响吗？似乎没有，因为一张纸和橡胶球可以被弯曲成不同的形状，但空间又不是一种物质。它当然必须是固定和绝对的。空间和时间也自然必须是欧几里得几何学的。

但是，值得注意的是欧几里得的公理只是假设。虽然直觉上它们对空间和时间是正确的，但假设可以是错的。其中一个重要假设就是，时间在宇宙的所有地方都是一样的。如果将两个时钟同步，无论它们是在以不同的速度运动，或者相隔光年远，它们的走时率都是一样的。但如果我们认为空间和时间是绝对的网格，那么我们测量物体的运动速度时就必须相对于该网格，包括光速。也就是说，如果你相对于背景网格在运动，你所测量的光的速度和你静止时测量的不一样。然而，实验结果却告诉我们空间和时间并不是绝对的，光才是。光在空间和时间之间产生了几何联系，联系空间和时间的几何规则就是光的速度是常数。