对于字符串来说,还有一种查询效率较高的数据结构,叫做Trie树。
比如我们有一系列的字符串:{bachelor#, bcs#, badge#, baby#, back#, badger#, badness#},我们之所以每个字符串都加上#,是希望不要一个字符串成为另外一个字符串的前缀。把它们放在Trie树中,如图所示。
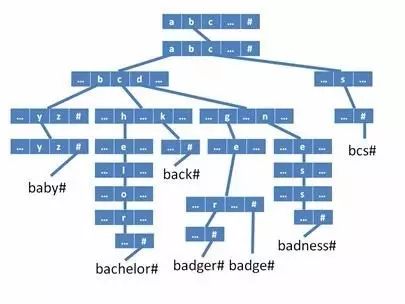
在这棵Trie树中,每个节点都包含27个字符。最上面的是根节点,如果字符串的第一个字符是“b”,则“b”的位置就有一个指针指向第二个层次的节点,从这一层的节点开始,下面挂的整棵树,都是以“b”开头的字符串。第二层的节点也是包含27个字符,如果字符串的第二个字符是“c”则“c”的位置也有一个指针指向第三个层次的节点,第三个层次下面挂的整棵树都是以“bc”为前缀的,以此类推,直到碰到“#”,则字符串结束。通过这种数据结构,我们对于字符串的查找速度就和字符串的数量没有关系了,而是字符串有多长,我们就顶多查找多少个节点,而字符串的长度都是有限的,所以查询速度是相当的快。
当然细心的同学也发现了,高速度的代价就是空间占用太大,而且是指数增加的,还是以27为底数的。好在还是英文啊,说破天不过就是26个字母,要是中文可怎么办啊。所以咱们可不能有没有的都列在哪里,出现的字符咱就占用空间,不出现的咱可不浪费。基于这种理念,上面的那棵Trie树就变成了图的样子。
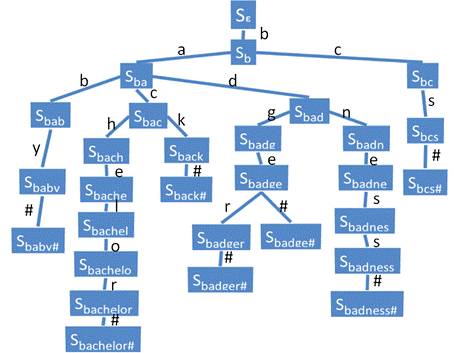
图中仅仅保留了已有的字符,并将每个节点变成了一种状态(State),在没有任何输入的情况下,我们处于根节点的状态,当输入字符“b”后,便到了下一层的状态S
b
,当再输入字符“a”后,就到了再下一层的状态S
ba
,所有在S
ba
下面挂着的整棵树都是以“ba”作为前缀的。
熟悉编译原理或者形式语言的同学已经发现了,这是一个有限状态机。不熟悉的同学也不要紧,很容易理解,假设有一个门,有两个按钮“开”和“关”,代表用户的输入,门有两种状态,“开着”和“关着”。门的状态根据用户的输入而变化,比如门处于“关着”的状态,用户输入“开”,就转换到“开着”的状态,然后再点“关”,就回到“关着”的状态。当然也可以识别不合法的输入,比如门本来就“开着”,你还猛点“开”这个按钮,门或者报错,或者没有反应。在上面的有限状态机中也是这样的,一开始处于根节点的状态,用户输入“b”,就进入状态S
b
,输入“c”,就进入状态S
bc
,再输入“s”,进入状态S
bcs
,最后用户输入“#”,字符串结束,进入状态S
bcs#
,说明字符串“bcs#”在我们的状态机里面是合法的,存在的。如果用户输入“b”之后输入“z”,在状态机中没有对应的状态,所以以“bz”开头的字符串是不存在的。通过我们的这个有限状态机,同样能够起到查询字符串的作用。
其实这个状态机还可以进一步简化。我们发现有的状态是有多个后续状态的,比如S
bac
,根据输入的不同进入不同的后续状态,而有的状态的后续状态是唯一的,比如当用户到达状态S
bach
,此后唯一的合法输入就是“elor#”,所以根本不需要一个个的进入状态S
bache
,S
bachel
,S
bachelo
,S
bachelor
,直到状态S
bachelor#
才发现用户输入是否存在,而是在到达状态S
bach
之后,直接比较剩余的字符串是否是“elor#”就可以了,所以上面的有限状态机可以变成图的样子,所谓的剩余的这些字符串,我们称之为后缀。
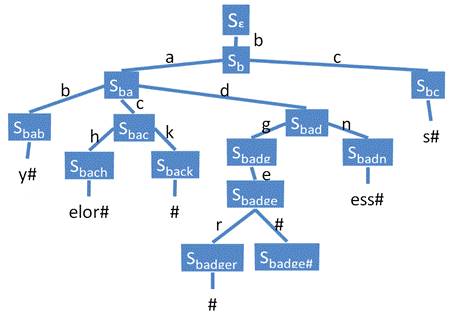
接下来的任务,就是如何将这个简化了的树形结构更加紧凑的保存起来了。我们在这里要介绍一种不需要占用太多空间的Trie树的数据结构,双数组Trie树。
顾名思义,双数组Trie树就是将上述的树形结构保存在两个数组中,那怎么保存呢?
我们来看上面的这个树形结构,多么像咱们的组织架构图啊,最上面的根节点是总经理,各个中间节点是各部门的经理,最后那些后缀就是咱们的员工了。现在公司要开会了,需要强行把这个树形结构压扁成数组结构,一个挨一个的坐,那最应该要维护的就是上下级的关系。对于总经理,要知道自己的直接下级,以及公司有多少领导干部。对于中层领导,一方面要知道自己的上级在哪里坐,下级在哪里坐;对于基层领导,除了知道上级在哪里坐,还需要知道员工在那里坐。
双数组Trie树就是一个维护上下级关系的一个数据结构。它主要包含两个数组BASE和CHECK,用来保存和维护领导干部之间的关系的,另外还有一个顺序结构TAIL,可以在内存中,也可以在硬盘上,用来安排咱们员工坐的。更形象的说法,两个数组就相当于主席台,而员工只有密密麻麻坐在观众席上了。
BASE和CHECK数组就代表主席台上的座位,如果第i位,BASE[i]和CHECK[i]都为0,说明这个位置是空的,还没有人坐。如果不是空的,说明坐着一位领导干部,BASE[i]数组里面是一个偏移量offset,通过它,可以计算出下属都坐在什么位置,比如领导S
b
有两个下属S
ba
和S
bc
,如果领导S
b
坐在第r个位置,则BASE[r]中保存了一个偏移量q(q>=1),对于下属S
ba
,是由S
b
输入“a”到达的,我们将字符“a”编号成一个数字a,则S
ba
就应该坐在q+a的位置,同理S
bc
就应该坐在q+c的位置。CHECK[i]数组里面是一个下标,通过它,可以知道自己的领导坐在什么位置,比如刚才讲到的下属S
ba
,他坐在q+a的位置,他的领导S
b
坐在第r个位置,那么CHECK[q+a]里面等于r,同理CHECK[q+c]里面也应该是r,那BASE[q+a]和BASE[q+c]中保存的什么呢?当然就是S
ba
和S
bc
他们的下属的位子了。所以职场中,每个人都同时扮演两种角色,一方面是上司的下属,一方面是下属的上司,所以每个位子i都有两个数字BASE[i]和CHECK[i],坐在每个位子上的人都应该知道,自己的上司是谁,下属是谁。
对于基层领导稍有不同,因为基层领导的下属就是普通员工了,不坐在双数组主席台上了,而是坐在TAIL观众席上了,所以对于基层领导,如果他坐在第i个位置,则BASE[i]就不是正的了,而是一个负的值p,表示他是基层领导,在双数组主席台上 没有下属了,而|p|则表示基层领导所下属的哪些普通员工在TAIL观众席上的位置。
至于TAIL观众席的结构,就非常简单了,普通员工嘛,别那么多讲究,一个挨一个的做,用$符合进行分割。
根据上述的原理,上面的那颗树保存在双数组里面应该如图,至于这里面的数据如何形成,下面会一步一步详细说明:
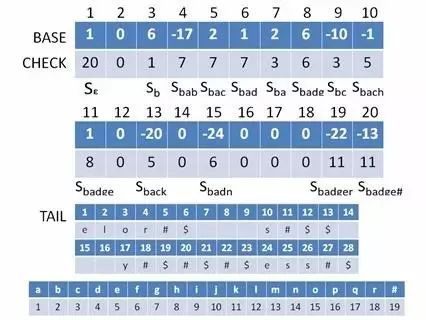
图中的最下方是对每个字符的编号。从图中我们可以看出,总经理S
ᵋ
总是坐在头一把交椅,CHECK[1]=20,主席台总共有20个位子,总经理当然应该对干部的总体情况有所把握。总经理的下属S
b
坐在BASE[1]+b = 1+2=3的位子上,S
b
的上司是总经理,所以CHECK[3]=1,S
b
的下属有两个S
ba
和S
bc
,他们的座位BASE[3]+a=6+1=7以及BASE[3]+c=6+3=9,自然CHECK[7]和CHECK[9]都等于3,以此类推。有人可能会困惑为什么BASE[1]是1而BASE[3]是6,不是1也不是5呢?这是在安排座位的过程中逐渐形成的,从下面双数组Trie树的形成过程大家会更详细的了解,在这里就简单说明一下,对于每一个坐在第i个位置的领导,BASE[i]里面都保存下属相对于他的offset,当然每个领导都希望offset越小越好,这样自己的下属也能坐在前面,对于总经理来说,当然他最牛,所以BASE[1]可以取最小值1,因为总经理刚坐下的时候,主席台是空的,他的下属随便坐都可以,对于其他的领导干部就不一定了,如果BASE[i]取1,结果计算后给自己的下属安排位置的时候,发现位置以及被先来的人坐了,所以没办法,只有增加BASE[i],让自己的下属往后坐坐。对于状态S
bab
,S
bc
,S
bach
,S
back
,S
badn
,S
badger
,S
badge#
,他们的BASE[i]都是负的,所以他们是基层领导,通过BASE[i]里面的值的绝对值,可以找到TAIL观众席中自己的下属,比如S
bab
的BASE值为-17,在TAIL中第17个字符开始是“y#$”,所以连接起来就是“baby#”。当然TAIL中也有一些很奇怪的,比如第20和第22个都只保存了“#$”,这说明了,除了结束符“#”之外,在最后一个字符才与其他的字符串做了区分,第20个就是这样的,“back#”到了字符“k”才和“bachelor#”有所区分(“back#”和“bachelor#”都是以bac为开头的,都归S
bac
领导,必须提拔字符“k”和“h”到主席台,形成状态S
back
和S
bach
来区分两个团队),既然分开了,就是一个单独的团队,虽然后面只跟了一个“#”,S
back
作为一个小小领导,也需要等上主席台,别拿村长不当干部。其实还有更惨的,对于第13个,就只剩下分隔符“$”,这是因为“badge”完全是另外一个字符串“badger”的前缀,多亏加了个结束符“#”才将两者区分开来,对于“badge#”来讲,到了“#”字符才区分,那么只好也做上主席台,做个光杆司令了。还有一点奇怪的就是,TAIL中为什么有空位置啊,比如位置7,8,9?这是历史原因造成的,因为一开始字符串“bachelor#”刚来的时候,其他的字符串还没来,公司规模较小,就一个团队,不需要那么多层领导,所以就S
b
作为唯一的一个团队的头坐主席台,其他的“achelor#”都坐观众席,所以“achelor#$”总共占了9个位置,后来“bcs#”来了,光是领导S
b
不足以区分这两个字符串团队“bachelor#”和“bcs#”(他们都是以b开头的啊),所以“achelor#”中的字符“a”和“bcs#”的字符“c”都被提拔为领导岗位,对两个字符串团队以作区分,就形成了状态S
ba
和S
bc
(从此“bachelor#”可以说我们是以ba开头的,而“bcs#”可以说我们是以bc开头的),后来“back#” 来了,仅仅字符“ba”以及“bac”都不足以区分“bachelor#”和“back#”,所以,不但“bachelor#”中的字符“c”被提拔成领导岗位,形成状态S
bac
,字符“h”也被提拔,形成状态S
bach
,从而员工就剩下了“elor#”,被提拔了三位,所以位置7,8,9就空下来了,那为什么不让后面的字符跟上呢?一方面,在双数组主席台中,其他团队的下属的位置都已经标好了,这一跟上都要改,比较麻烦,另外一方面,TAIL很可能保存在硬盘文件中的,将文件中的内容移动,也是很低效的事情。
有了上述结构,对字符串进程查询就方便了,一般按照以下的流程进行:
//输入: String inputString=”a
1
a
2
…… a
n
#”转换成为int[] inputCode
boolean doubleArrayTrieSearch(int[] inputCode) {
int r=1;
int h=0;
do {
int t = BASE[r] + inputCode[h];
if(CHECK[t] != r){
//在双数组中找不到相同前缀,说明不存在与这个集合
// a
1
a
2
…… a
h-1
都相同,a
h
不同
//座位t上坐的不是你的领导,在这棵树上这个字符串找不到组织
return false;
} else {
//前缀暂且相同,继续找下一层状态
// a
1
a
2
…… a
h
都相同,下个循环比较a
h+1
//说明你属于这个大团队,接着看是否属于某一个小团队
r = t;
}
h = h + 1;
} while(BASE[r]>0)
//到这一步双数组中的结构查询完毕,BASE[r]<0,应该从TAIL中查找了
If(h == inputCode.length - 1){
//如果已经到了结束符#,说明这个字符串所有的字符都在双数组中,是个光杆司令
Return true;
}
Int[] tailCode = getTailCode(-BASE[r]);//从TAIL中拿出后缀
If(compare(tailCode, inputCode, h+1, inputCode.length -1) == 0){
//比较TAIL中的字符串和inputCode中剩下的”a
h+1
…… a
n
#”是否相同,相同则存在
Return true;
} else {
Return false;
}
}
接下来,我们就来看看这种微妙的数据结构是如何构造的。其实构造过程说起来很简单,就是一开始整个双数组中只有根节点,然后随着字符串的不断插入而形成。要插入一个新的字符串,首先还是要调用上面的代码进行搜索一下的,如果能够搜索出来,则这个字符串原来就存在,则什么都不做,如果没有搜索出来,就需要进行插入操作。根据上面的搜索程序,搜索不出来分为两种情况,也就是上面的程序中返回False的地方
1) 第一种情况是在双数组中找不到相同的前缀。也即对于输入字符串a
1
a
2
… a
h-1
a
h
a
h+1
… a
n
#,在双数组中,a
1
a
2
… a
h-1
能找到对应的状态S a
1
a
2
… a
h-1
,然而从a
h
开始,找不到对应的状态S a
1
a
2
… a
h-1
a
h
,所以需要将S a
1
a
2
… a
h-1
a
h
作为S a
1
a
2
… a
h-1
的下属加入到双数组中,然后将a
h+1
… a
n
#作为S a
1
a
2
… a
h-1
a
h
的员工放到TAIL中。然而加入的时候存在一个问题,就是原来S a
1
a
2
… a
h-1
已经有了一些下属,并经过原来排位置,找到了合适的BASE值,通过它能够找到这些下属的座位。这个时候状态S a
1
a
2
… a
h-1
a
h
来了,当它想要按照BASE[r] + a
h
=t找到位置的时候,发现CHECK[t]不为0,也即位置让其他先来的人占去了。这个时候有两种选择,一种选择是改变自己的领导S a
1
a
2
… a
h-1
的BASE值,使得连同S a
1
a
2
… a
h-1
a
h
和其他的下属都能够找到空位子坐下,这就需要对自己的领导S a
1
a
2
… a
h-1
的原有下属全部迁移。另一种选择就是既然CHECK[t]不为零,说明被别人占了,把这个占了作为的人迁走,我S a
1
a
2
… a
h-1
a
h
还是坐在这里,要迁走位置t的人可不容易,要先看他的领导的面子,也即根据CHECK[t]=p找到他的领导的位置,迁移位置t的人,需要改变他的领导的BASE[p],而BASE[p]的改变,必将导致他的领导的原有所有下属都要迁移,另找 位置。那么选择哪一种方式呢?要看哪种方式迁移的人数少,就采取哪种方式。




