选自arXiv
作者:Yoav Levine等
机器之心编译
参与:吴攀
深度学习和量子物理是两个看似关联很小的领域,但研究者还是找到了它们之间的共同之处。近日,耶路撒冷希伯来大学的几位研究者的一篇论文《Deep Learning and Quantum Physics : A Fundamental Bridge》介绍了他们的发现:深度卷积算术电路(ConvAC)所实现的函数和量子多体波函数之间存在某种等价性。机器之心在本文中简要地编译介绍了这项研究,论文原文可点击文末「阅读原文」查阅。

深度卷积网络已经在许多不同的机器学习应用中取得了前所未有的成功。是什么让这些网络如此成功?研究正在逐渐揭开其中的秘密,但其中大部分仍然还是有待揭秘的重要奥秘。归纳偏置(inductive bias)就是其中之一,其反映了嵌入在网络架构中的先验知识(prior knowledge)。在这项研究成果中,我们建立了量子物理学领域和深度学习领域的一种基本(fundamental)联系。我们使用这种联系断言了全新的理论观察,该观察是关于卷积网络每一层的通道(channel)的数量在整体的归纳偏置中的作用。具体来说,我们给出了深度卷积算术电路(ConvAC:convolutional arithmetic circuit)所实现的函数和量子多体波函数(quantum many-body wave function)之间的等价性,这取决于它们共同的基础张量结构。这有助于将量子纠缠度量(quantum entanglement measures)用作深度网络表达能力(以建模其输入的复杂相关性结构)的定义良好的度量方法。最重要的是,构建张量网络(Tensor Network)方面的深度 ConvAC 成为了可能。这种描述让我们可以进行一个卷积网络的图论分析(graph-theoretic analysis),通过这种方式我们展示了一种通过深度网络的通道数量直接控制深度网络的归纳偏置的方法,这些通道是其基本图中的相关最小切割(related min-cut)。对任何为特定任务设计卷积网络的实践者来说,这个结果是有用处的。我们对 ConvAC 进行了理论上的分析,并且在更常见的卷积网络(ConvNet)(涉及到 ReLU 激活和最大池化)上通过实验验证了我们的发现。除了上面描述的结果,这项工作也提出了两个跨学科的桥梁:用良好定义的图论工具对深度卷积网络的描述和与量子纠缠的形式连接。
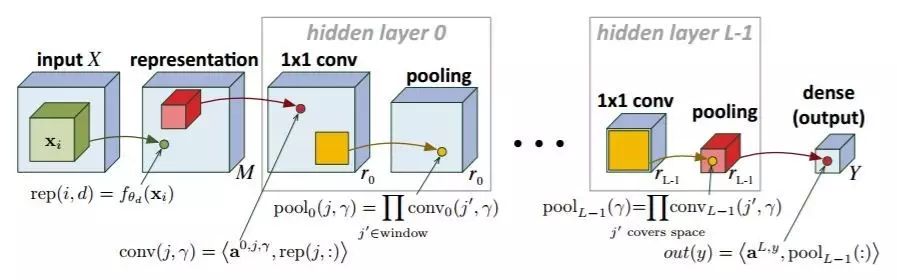
图 1:Cohen et al. (2016b) 提出了原本的卷积算术电路网络(Convolutional Arithmetic Circuits network)
3. 量子波函数与卷积网络
当描述一个由多个相互作用的粒子所构成的系统(被称为多体量子系统(many-body quantum system))的量子力学性质时,物理学家需要使用能够表示许多输入和一个输出之间的复杂关系的函数。类似地,监督学习或无监督学习等机器学习任务也需要使用能够表示许多输入(如图像的许多像素)和一个输出之间的复杂关系的函数。这一章我们将对这种类比进行公式化。在简单介绍了物理学家用来描述多体系统的量子力学性质的符号之后,我们说明了如何将 ConvAC 所实现的函数(式 2 和 式 3)与 N 个粒子的量子波函数在数学上等价起来。通过由 ConvAC 所带来的对深度卷积网络的张量描述,这在机器学习和量子物理这两个看似无关的领域之间构建了一种可靠的结构联系。我们遵循了 Preskill (1998) 中的相关推导,感兴趣的读者可参阅 Hall (2013) 获取对量子力学的全面数学介绍。
4. 纠缠和相关性的测量
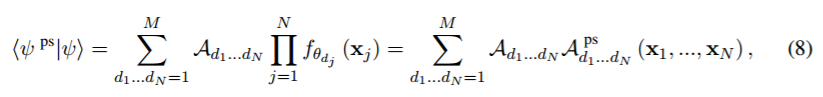
多体波函数和 ConvAC 所实现的函数之间的形式联系(如式 8 所示)让我们有机会使用已有的物理见解和工具来分析卷积网络。对于表征多体波函数的粒子间的相关性结构,物理学家给予了特别的关注,因为其对被观测系统的物理性质有广泛的影响。尽管机器学习领域对这个问题的关注较少,但我们可以直观地理解:在解决一个机器学习问题时,应该考虑表征该问题的相关性,比如数据集中典型图像的像素之间的相关性。我们应该看到,对于函数的「表达力(expressiveness)」的需求实际上是对该函数建模相关复杂相关性结构的需求,不管这个函数是卷积网络实现的,还是等价的多体波函数。在这一节,我们首先介绍了物理学家量化相关性的方法,然后讨论了可以如何将这些方法用于机器学习领域的分析。
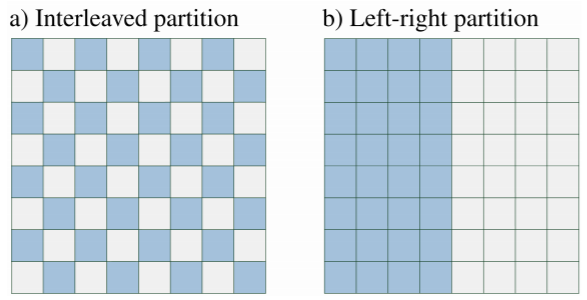
图 2:图片为 8×8 大小。a) 交错分区的图示,b) 左右分区的图示。如果你希望建模图像(比如面部图像)的两边之间的复杂相关性结构,那么该网络应该支持左右分区的高纠缠测量(high entanglement measure);如果你希望对邻近像素这样做(如自然图像),那么应该选择交错分区。在第 7 节,我们说明了这种对卷积网络的归纳偏置的控制可以如何通过适当调整每一层的通道数量来实现。
5. 张量网络和张量分解
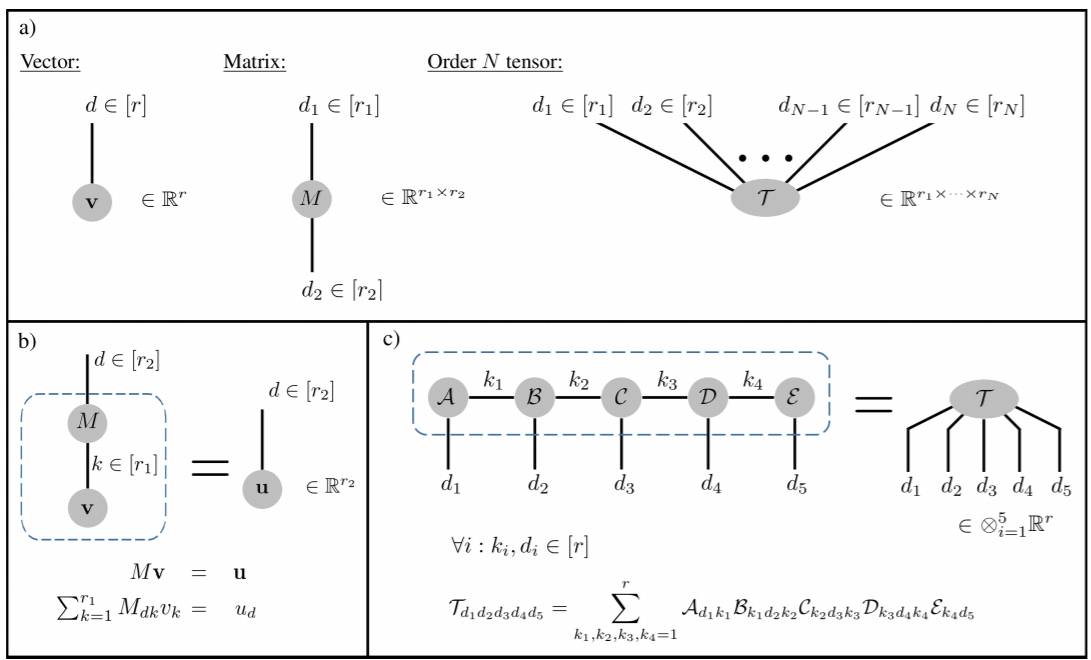
图 3:张量网络(TN/Tensor Networks)的简单介绍。a) 该张量网络中的张量用节点表示,节点的度(degree)对应于由其所表示的张量的阶数。b) 用 TN 符号表示的一个矩阵乘一个张量。收缩(contracted)指数用 k 表示并且相加。开放(open)指数用 d 表示,它们的大小等于由整个网络所表示的张量的阶数。所有这些指数的值都在 1 到它们的连接维度(bond dimension)之间。收缩(contraction)用虚线标示。c) 一个更加复杂的例子——一个网络使用在稀疏互连的低阶张量上的收缩表示一个更高阶的张量。该网络是一种分解(decomposition)的简单案例,其在张量分析社区被称为张量训练(tensor train,Oseledets (2011)),而在凝聚态物理学界则被称为矩阵积态(matrix product state,参见 Orús (2014))。
6. 一个用作张量网络的卷积网络
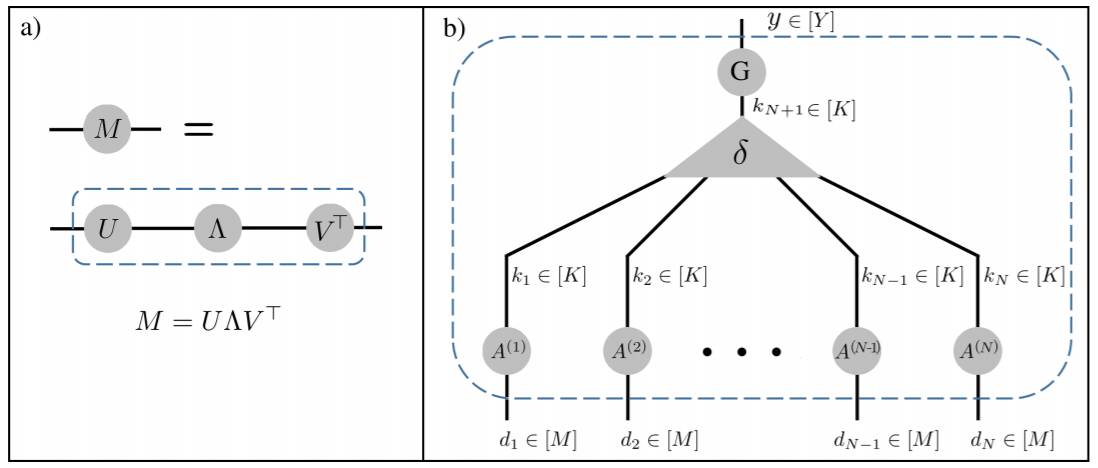
图 4:a) 张量网络(TN)形式的奇异值分解。Λ 节点表示一个对角矩阵、U 和 V 节点表示正交矩阵。b) 相当于 CP 分解的 TN。
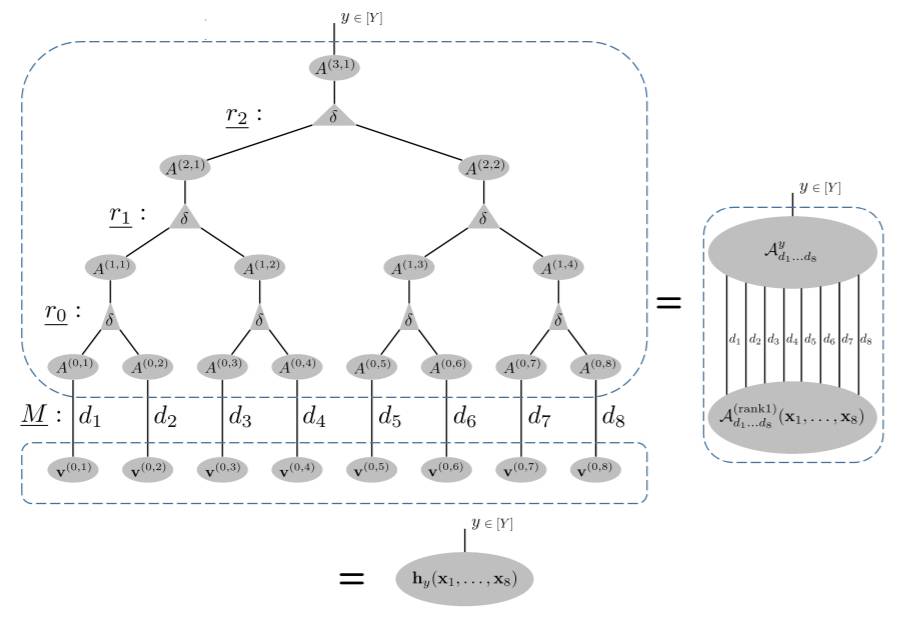
图 5:相当于 HT 分解的 TN,其带有对应于图 1 的 ConvAC(N=8)的计算的相同通道池化方案,详见 6.2 节 
原文链接:https://arxiv.org/abs/1704.01552v1
本文为机器之心编译,转载请联系本公众号获得授权。
✄------------------------------------------------
加入机器之心(全职记者/实习生):[email protected]
投稿或寻求报道:[email protected]
广告&商务合作:[email protected]

















