如何衡量变量之间的相关性？

我们都知道，大数据的机遇和挑战主要有三个方向：海量、高速与多样性。在我们获取到的海量数据中，与目标变量可能相关的影响变量自然也很多。那么，有必要全部的变量都放进来分析吗？在数据分析的建模过程中，如何对变量进行取舍？在变量的选择中，又用什么来衡量变量之间相关性的强弱程度呢？

在实际的数据分析工作中，我们通常需要同时结合技术和业务两方面来判断变量之间的相关程度，选择相关程度比较高的部分变量来进行建模分析。

业务判断重要吗？当然，骨干们累积的工作经验永远是无价之宝，是无法用数据来表达或衡量的财富，他们提出的建议能够给出数据分析无法传达的信息，对判断变量的相关性大有帮助。不过，我还是认为，技术才是判断的根本和基础。如果说业务判断是一朵鲜花，从统计专业的角度、客观量化变量之间的相关性就是绣着花的锦缎。

在各领域的相关性分析中，应用最广泛的当然要数 Pearson 相关系数了，也就是我们俗称的相关系数。相关系数能这样受欢迎，当然有其无法忽视的优点，比如便于操作、容易理解等；然而，相关系数也有自己的缺陷：一是仅能衡量变量之间的线性相关程度；二是两个变量的方差都不能为 0 。在实际工作中，很多变量之间的相关性并不是线性相关的关系；另外，许多金融数据往往是后尾分布，方差并不存在，这就使得 Pearson 相关系数顿时没了用武之地。

那么，除了 Pearson 相关系数之外，还有没有其他的指标可以衡量变量之间的相关性呢？ 这里我们就来介绍两个指标：

（ 1 ）从概率角度提出的方法，这个指标特别适合金融数据，由于是著名统计学家张尧庭教授提出的，就姑且命名为“张氏系数”吧；

（ 2 ）从比重差值角度提出的匹配系数。

两个指标的共同优点是对数据的分布没有要求，都可以衡量两个变量之间的相关性。下面，我们一起看看它们的原理吧。

1）张氏系数：

对于 A 和 B 两个事件，从概率的角度有以下情况：

引申到两个变量 X 和 Y ，如果样本数据大部分是(x1-x2)(y1-y2)>0 ， 那么我们可以说 x 和 y 是正相关的关系；反之，(x1-x2)(y1-y2)<0占据多数时， x 和 y 是负相关的关系。在这个基础上可以生成一个衡量相关性大小的指标：

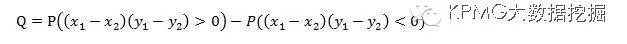
张氏系数 Q的 取值在 [-1 ， 1] 之间，取值越接近 1 ，正相关的程度越大；取值越接近 -1 ，负相关的程度越大。

2）匹配系数：

在比重差值的思想上提出的匹配系数主要用来衡量两个变量之间的比率相关性：

其中

，

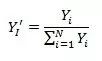M 的性质也比较好，取值是 [0 ， 1] 之间，取值越接近 1 ，比率相关的程度越大。

接下来，我们不妨将这两个指标在实际案例中应用一下。最近，我们团队的部分成员参加了阿里巴巴举办的 2016 年天池大数据竞赛 中的“ 需求预测和分仓规划大赛 ”，在处理数据的过程中，就用到了以上两种指标筛选变量。

这次竞赛中使用的数据是 商品从 20141010 到 20151227 的全国和区域分仓数据，商品在全国的特征包括商品的本身的一些分类，如类目、品牌等，以及历史上的一些用户行为特征，如浏览人数、加购物车人数、收藏人数、购买人数等。大赛要求参赛者需给出后面两周（ 20151228-20160110 ）的全国和区域分仓目标库存。

我们定义目标变量 Y 为某商品某天之后两周的全国非聚划算支付件数，自变量包括此商品某天之后一天的浏览次数、流量 UV 、被加购次数、加购人数、收藏人数、拍下笔数 、 聚划算引导浏览次数和聚划算引导浏览 等25个变量。我们选取商品 ID 为 197 的 25 个自变量、 378 天数据，想要通过相关性分析，知道这 25 个自变量与目标变量的相关程度大小。

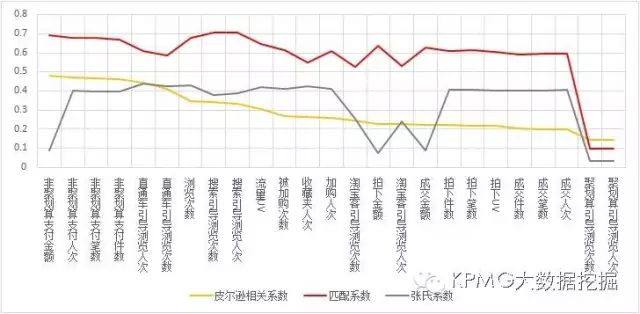
从上图可以看出，综合 三个系数来看，聚划算引导浏览次数和聚划算引导浏览人次这两个变量对 Y 的相关程度都最低，这与经验比较吻合，毕竟我们要考虑的是 非聚划算支付件数的问题