公众号ID
|
计算机视觉研究院
学习群
|
扫码在主页获取加入方式

论文地址:
https://arxiv.org/pdf/2111.13824.pdf
项目代码:
https://github.com/megvii-research/FQ-ViT
Column of Computer Vision Institute
将算法网络进行量化和模型转换可以显着降低模型推理的复杂性,并在实际部署中得到了广泛的应用。然而,大多数现有的量化方法主要是针对卷积神经网络开发的,并且在完全量化的vision Transformer上应用时会出现严重的掉点。今天我们就分享一个新技术,实现高精度量化的Vit部署。AI大模型落地使用离我们还远吗?
Transformer 是现在火热的AIGC预训练大模型的基础,而ViT(Vision Transformer)是真正意义上将自然语言处理领域的Transformer带到了视觉领域。从Transformer的发展历程就可以看出,从Transformer的提出到将Transformer应用到视觉,其实中间蛰伏了三年的时间。而从将Transformer应用到视觉领域(ViT)到AIGC的火爆也差不多用了两三年。其实AIGC的火爆,从2022年下旬就开
始有一些苗条,那时就逐渐有一些AIGC好玩的算法放出来,而到现在,AIGC好玩的项目真是层出不穷。
随着近两年来对视觉Transformer模型(ViT)的深入研究,ViT的表达能力不断提升,并已经在大部分视觉基础任务 (分类,检测,分割等) 上实现了大幅度的性能突破。然而,很多实际应用场景对
模型实时推理的能力要求较高
,但大部分轻量化ViT仍无法在多个部署场景 (GPU,CPU,ONNX,移动端等)达到与轻量级CNN(如MobileNet) 相媲美的速度。
因此,重新审视了ViT的2个专属模块,并发现了退化原因如下:
基于以上分析,研究者提出了Power-of-Two Factor(PTF)来量化LayerNorm的输入。通过这种方式,量化误差大大降低,并且由于Bit-Shift算子,整体计算效率与分层量化的计算效率相同。
此外还提出了Log Int Softmax(LIS),它为小值提供了更高的量化分辨率,并为Softmax提供了更有效的整数推理。
结合这些方法,本文首次实现了全量化Vision Transformer的训练后量化。
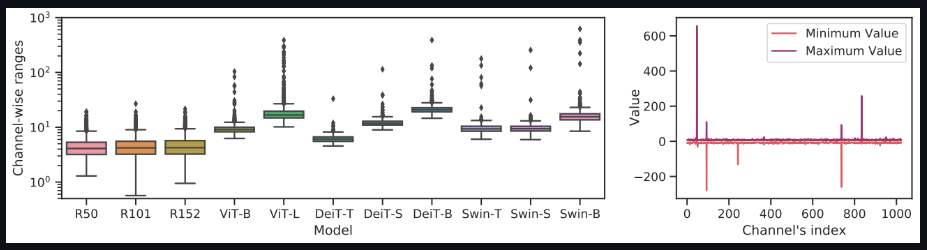
下面的这两张图表明,与CNN相比,视觉转换器中存在严重的通道间变化,这导致了分层量化的不可接受的量化误差。
首先解释网络量化符号。假设量化位宽为b,量化器Q(X|b)可以公式化为将浮点数X∈R映射到最近量化仓的函数:
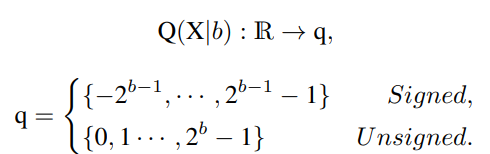
Uniform Quantization
Uniform Quantization在大多数硬件平台上都得到了很好的支持。它的量化器Q(X|b)可以定义为:
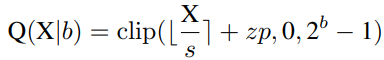
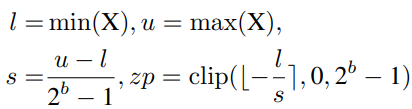
其中s(标度)和zp(零点)是由X的下界l和上界u确定的量化参数,它们通常是最小值和最大值。
Log2 Quantization
Log2 Quantization将量化过程从线性变化转换为指数变化。其量化器
Q(X|b)
可定义为:
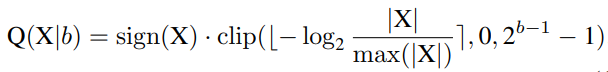
为了实现完全量化的视觉变换器,研究者对所有模块进行量化,包括Conv、Linear、MatMul、LayerNorm、Softmax等。特别是,对Conv、线性和MatMul模块使用均匀的Min-Max量化,对LayerNor和Softmax使用以下方法。
Power-of-Two Factor for LayerNorm
Quantization
在推理过程中,LayerNorm计算每个正向步骤中的统计量µX,σX,并对输入X进行归一化。然后,仿射参数γ,β将归一化输入重新缩放为另一个学习分布。
如刚开始解释分析一样,与神经网络中常用的BatchNorm不同,LayerNorm由于其动态计算特性,无法折叠到前一层,因此必须单独量化它。然而,在对其应用训练后量化时观察到显著的性能下降。查看LayerNorm层的输入,发现存在严重的通道间变化。
研究者提出了一种简单而有效的层范数量化方法,即
Power-of-Two Factor
(PTF)。PTF的核心思想是为不同的信道配备不同的因子,而不是不同的量化参数。给定量化位宽b,输入活动X∈RB×L×C,逐层量化参数s,zp∈R1,以及PTFα∈NC,则量化活动XQ可以公式化为:
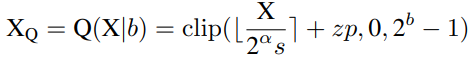
其中部分参数如下:
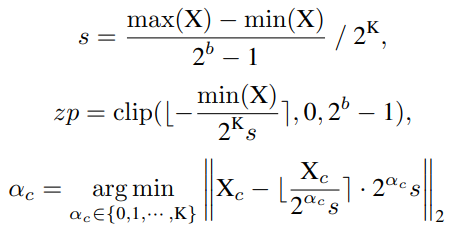
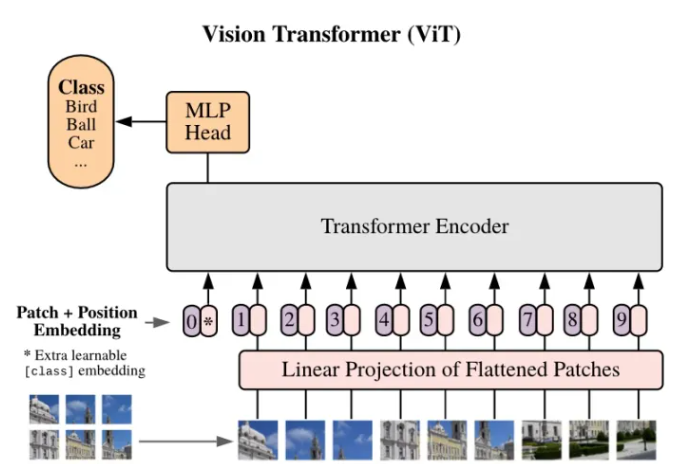
Softmax quantized with Log-Int-Softmax (LIS)
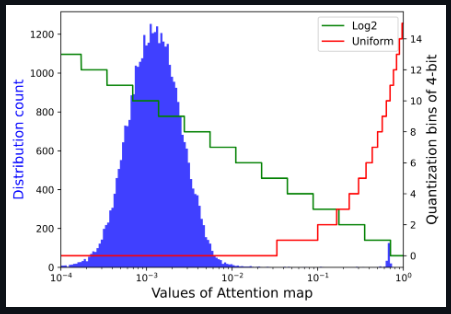
注意图的存储和计算是变压器结构的瓶颈,因此研究者希望将其量化到极低的位宽(例如4位)。然而,如果直接实现4位均匀量化,则会出现严重的精度退化。研究者观察到分布集中在Softmax输出的一个相当小的值上,而只有少数异常值具有接近1的较大值。基于以下可视化,对于具有密集分布的小值区间,Log2保留了比均匀更多的量化区间。

将Log2量化与i-exp(i-BERT提出的指数函数的多项式近似)相结合,提出了LIS,这是一个仅整数、更快、低功耗的Softmax。
整个过程如下所示。