从微观方面解析非注射用液体与半固体制剂放大效应

　　对工艺过程进行放大（或缩小），厂商做决定的最终依据是产品工艺的经济学，也就是原材料价格、人员费用、与生产有关的设备费用以及设备的操控费用。如果放大生产过程能够降低单个产品的生产成本，那么从经济学方面考虑是有益的，此过程将给厂商带来附加的经济效益。这样，工艺放大可能促使厂商快速将产品推进市场，或改进产品的市场的分布及反应，从而提高产品的市场占有率。在制药行业中，因为工艺放大具有潜在优势，你可能会认为多数制药厂会集中主要力量确保完成工艺放大。然而，与放大相关的出版研究报告和数据资料相对匮乏的现状提示情况并非如此。当然，从另一方面也可以认为公开性研究与数据匮乏的现象只不过反映了厂商以保密手段维持竞争优势的需求。

　　然而，对于参考文献不足的现象，人们也可以归因于制药加工过程中的单元操作的复杂性。如果制药技术人员认为放大只是比例问题，即：

放大比例=大规模生产率/小规模生产率

　　那么解决放大问题，只能说是维持在反复试验，不断调试的工作，而不是通过科学的方法解决。1998年，在一篇分散系统放大方面的专题论文中，Block指出：制药过程包括多种类型的单元操作（例如：混合、转移等），这一特点造成生产过程的复杂性，最终导致不能根据简单的外推法，从实验室或调试阶段推算到生产商品的水平。

　　“一个单元操作与另一个单元操作的成功衔接，限定了整个制备过程的功能性。对于每一个单元操作，都可以按照一定的比例进行放大或缩小，然而对于复合制造过程却行不通是因为每个单元操作具有不同的有效放大比例。正因如此，单元操作的放大与复合操作过程的放大之间存在分歧，而这种不同可能导致在放大过程中出现一些料想不到的问题。不仅如此，一些在小规模过程中无关紧要的问题可能存在于商品中。例如：只有生产大M-商品的时候，我们才会遇到产品的储存和装卸问题；而且在进行大批址生产过程时会产生热量，此热量可能超过系统的散热能力，上述问题都是不能通过小规模试验预测的。”

（单元操作与单元操作衔接图示例）

　　此外，当操作规模增加时，单元操作可能成为限速步骤。20世纪80年代中期，AstaritaE41曾谈到：“放大的运算法则是不存在的，也就是说我们不能通过小规模的结果预测大规模的生产过程”，这句话概括了所有放大问题的结果。

　　液体制剂和半固体制剂的生产过程中都含有复合单元操作，认识到此点是解决两制剂放大问题的线索。进一步考察核心单元操作可以发现，根据考察范围的不同，即微观水平(JIM-cm)或宏观水平(cm-m)，工艺过程中的流动状态和黏度可发生多个数量级的改变。综上考虑，进行有效放大操作的关键是对宏观和微观迁移现象的正确评价和理解。例如掌握迁移现象中的扩散和总体流量。扩散引起的转运是指：由电子、原子和分子等微观移动产生的特性流动，即质量、热能、动力、电磁能等从高浓度区域流动到低浓度区域。然而，无论是平流还是对流，总体流量都包括：宏观条件下的特性流动以及在人工（机械搅拌）或自然（密度差异）条件下的整体特性流动。

　　1.液体与半固体中的迁移现象及放大与单元操作的关系

　　在过去近四十年中，一些实质性的努力使迁移现象的研究受益匪浅。具体而言，主要是以计算机模拟试验和迁移现象理论模型为基础的基本理论知识取代了通过经验所得的理论。这些重大成就源于1960年Bird等困公开发表的第一版经典专著，在此专著中，重点对三种主要传递(质量传递、动量传递和动力传递)类型的关系进行了研究。与一般扩散方程一致，所有传递现象都是遵循相同的模式。流量（无量纲是）或一定方向单位面积上的总迁移速率。可以用梯度相乘的系统特征表示：

　　式中，Γ一单位体积内性质Q（质量、热能和电能等）的浓度，即r=Q/V；t一时间；x一迁移的距离；占一广义扩散系数；E一迁移梯度或驱动力。

　　质量和热量传递可以用各自浓度Q与V的比值表示，其中质量m的浓度可直接确定，而热量浓度需要经下式计算得出：

　　式中，C一比热容量；T一温度。假设ρC是常数，那么在广义扩散方程中ρCT项就可以消除ρC，从而通过温度确定热量浓度。根据上述方法类推，应用自身的导数可以替代时间偏导数，因此动力传递可以用动力浓度µ来表示：

　　式中，v--动力学钻度。考虑到压力和重力作用，可以应用Navier-stokes关系式，以此控制牛顿流体动力学。

　　如果流量Γ是通过三维空间评价计算，那么可由下式表示：

　　Griskeycl指出：在最简单情况下，可以分别用Fick's扩散定律和Fourier's热传导定律表达热传递和质量传递特征。作为向量，它们都在三维空间x、y、z方向上具有一定的强度。然而，动量或流量归属于张量，需要通过9个变量确定其值，而不是3个变量。所以与牛顿流体定律类似，即使在最简单的传递情况下，其也具有比较复杂的特征：

　　式中，гyx一x轴方向的剪切应力；（dvx/dy）—切变速率；η一牛顿流体粘度系数。即广义扩散方程的解为г=f（t，x，y，z）

　　以抛物线的偏微分方程的形式表示。如果现象越复杂（例如模型中存在局部对流传递现象），就越难对广义扩散方程进行分析解答。然而，当把微分方程转变成代数形式时，则比较容易得到方程的数字解。

　　2.传递现象及其与复合单元操作之间的关系

　　正如上文提到的，所有的液体和半固体制剂产品的生产过程都包括复合单元操作。实际上，大量事实已经证明复合过程是主要的单元操作。甚至其间接作用，例如在热传递方面，也可能作为生产过程的基础。然而，对于混合过程的机械学研究和定量描述，至今仍不完善。尽管如此，根据充足的基本原理和经验数据还是可以进行合理的预测。

　　动态混合设备呈现多样性：搅拌叶轮由动态或移动的叶片构成，主要形式有推进刮板式、涡轮式、桨式、螺旋带式、型叶片式和螺旋杆式等。此外，还可以通过对搅拌叶轮的数目、每个叶轮的叶片数、叶轮叶片的螺距和搅拌叶轮的位置等的调整，使混合设备的性能达到令人满意的程度。与搅拌叶轮的样式相比较，分散装置或转子/定子的形状对混合过程的作用更强，不仅如此，棍合操作也可以通过喷射混合机或静态混合设备完成。如今，混合设备的选择十分混乱，此种情况导致无法实现有效的放大。虽然混合设备种类越来越多，但是通过对混合速率和程度以及流动规律的评价，我们还是可以找到共性间题进行比较。

　　低黏度系统中，易溶液体的混合是通过传递过程实现的，即未混合原料经流动（主体流或对流）传递到混合区域（高剪切应力或充分混合区域）。换言之，混合过程的质量传递取决于己知路径的层流和湍流（无数、大小不一的漩涡和回旋移动）。高强度的湍流混合多数发生在搅拌叶轮区域，液体的流动驱使新鲜液体流入该区。综上所述：混合过程的特征是以混合设备中液体的流动规律为基础的。Reynold对管道中液体流动的经典研究表明：一旦超越无量纲比率变量的临界值，流动就从层流变为湍流。此比率称为雷诺数，NRe可用下式来表示：

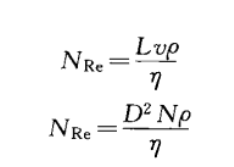
　　式中，p一密度；η一牛顿流体的黏度；v=速率；L一特性长度。式表示搅拌叶轮的雷诺数；D一搅拌叶轮的直径；N一搅拌叶轮的转速。NRe表示流动过程中惯性力与粘性力之比。当流体的流动占主导地位时，NRe值较高，反之，流体的黏度占主导地位时，NRe值较低。因此，从层流到湍流的转变过程受到流体的密度和黏度、平均速率和流动区域的大小（管道的直径，沉降微粒的直径）等因素的控制。对于直的圆柱形管道来说，当NRe<2100时，产生层流；当NRe>4000时，产生明显的湍流。当2100

　　在湍流中，漩涡随着组分的速度快速移动，这一速度是与参考点（流动液体表面）垂直的速度。因为漩涡的快速移动，所以湍流区域内的质量传递快于层流区域内分子扩散作用的结果，从而导致湍流区域的浓度梯度比层流区域的小。最终结果是湍流条件下的混合效率更高。然而，技术人员也应该牢记湍流具有的不利因素：例如漩涡数目增多，伴随着空气的介入，剪切应力的增加以及分散相中粒度分布的相应变化等。

　　在制药工业中，虽然一定范围内应用了连续的混合操作，但是多数液体和半固体制剂的生产过程，都是在搅拌槽或管道中通过分批操作实现的。虽然在制药企业和化妆品企业中，喷射或静态混合设备的使用逐渐广泛（长期用在化工企业中），但是我们将重点集中在分批操作过程，以下的混合过程都是由带搅拌叶轮的动态混合器完成。

　　混合器与泵的功能相同，混合器提供的功率通过搅拌叶轮传递到整个系统中，同时此功率与泵效应属于同类，均可以通过剪切应力和流体特性表示：

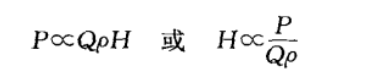
　　式中，P一搅拌叶轮输出功率；Q一流经混合设备的流体速度(泵出容量)；产一物质的密度；H一速度剪切应力。因此，在已知功率的条件下，剪切应力与容量成反比。

　　输人机械搅拌功率可通过Np计算：

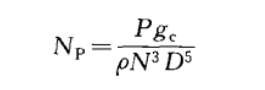
　　搅拌叶轮尺寸要与搅拌槽的大小成比例，这点也是十分重要的。如果搅拌叶轮直径D与搅拌槽直径T的比值较大（D/T>0.7），那么混合效率将很低。分析降低的原因，主要是因为搅拌叶轮与搅拌器壁之间的空间太小，使得液体回流路径受阻，最终导致不能产生较强的轴向流动。然而，在上述情况时，我们可以增加搅拌叶轮速度，以达到增强混合效果的目的，但是此过程还需要考虑到搅拌叶轮的厚度与角度的限制。相反，如果D/T的值太小，则搅拌叶轮在搅拌槽中不能产生合适的流速。

　　如果从雷诺数NRe的函数方面考虑系统行为，那么我们在混合操作方面将受益匪浅。图中用无量纲参数[无量纲速率，v'=v/ND；泵的抽吸量，NQ=Q/ND3；能量数，NP=（Pgc/PN3D5）；无量纲混合时间，t=tmN]表示NRe的对数函数。从公式角度考虑，虽然密度、黏度、混合容器的直径和搅拌叶轮的转速都是独立变量，但在引入雷诺数之后，以上几个变量之间就具有明显的内部关系。

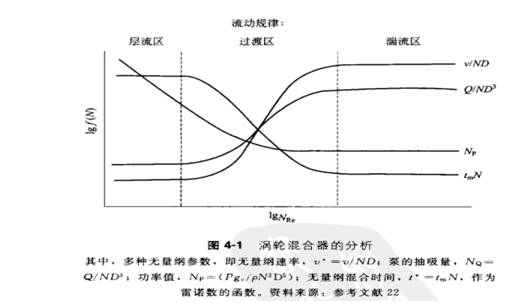
　　混合时间系指对预定质量实现混合所需要的时间，混合速率系指混合最终状态所对应的速度。对于一定配制的设备而言，混合时间tm由原料的性质和操作变量决定。而对于几何相似系统，如果系统的几何量纲可以按一定比值转变，那么混合时间就可以用无量纲数表示，即无量纲θm或tmN。

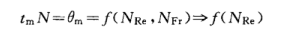
　　弗洛德数与NRe相似，表示作用在液体单位面积上的惯性力与重力的比。只有当密度差存在时，上式得出的这一结论才能够成立。当密度不存显著差异时（例如，乳剂的密度差异小于混悬剂）。方程中NFr项可以忽略不计。如图4-1中直线所示，无论是油流区还是层流区，无量纲的混合时间均与NRe值无关。然而，从组分流变学性质和设备几何学考虑。文献中有关θm灵敏度的数据存在一定分歧。所以必须把上式看作混合操作的简化。因此，在特殊情况应用此关系式时，需要慎重考虑。

　　在搅拌容器中。流动样式可能是放射状、轴向式或是沿着搅拌叶轮的切线方向。比较而言，锥个系统的速度方向和强度对流动样式的影响较强。尤其是在过渡区；如图4-1所示，在层流或湍流区内，无且量纲速率v或v/ND是常数，但在过渡区内速率在很大程度上取决于NRe。切向流或环状流最初产生的流动样式是小半径的辐射状或轴向流动，这种流动与淡涡的产生及最小限度的混合有关，甚至在多相系统中。还与微校的分层和分类有关。在整个系统中，我们通过挡板或定位的搅拌叶轮改变流体的方向。使流体偏离中心而流入搅拌槽，从而降低或消除激涡的产生。一定条件下，大容器比小容器更易产生游涡。因此，在过渡区，虽然小规模（实验室或中试工厂规模）条件下不盆要安装挡板，但在大规模生产中搅拌槽很可能需要安装挡板。

　　由于分散系统属于多相体系，且与牛顿流体相比具有较大的行为偏差。所以在分散系统（乳剂、混悬剂）生产过程中，混合过程较低黏度易溶液体的混合操作更为复杂。在系统的不同区城，同时产生层流和油流的现象很常见。在某些区城内，流动规律可能处于过渡区。也就是，既不是层流区也不是湍流区，而是两者之间。在放大过程中，应用变化的流动规律是十分重要的。但值得注意的是，只有充分进行布朗运动的时候，才能在分子水平达到均匀一致，此时混合过程进行得较完全。

　　未完，待续……

　　摘自书籍：《制剂工艺放大》第二版，【美】M.莱文（M.levin）主编（唐星等译）

　　备注：本文不存在商业用途，仅在于同行交流学习