
大数据文摘作品,转载要求见文末
翻译 | 张静,大力
校对 | 元元 时间轴 | 弋心
后期 | 郭丽(终结者字幕)
后台回复“字幕组”加入我们!
人工智能中的数学概念一网打尽!欢迎来到YouTube网红小哥Siraj的系列栏目“The Math of Intelligence”,本视频是该系列的第二集,讲解优化问题和常用便捷优化方法。后续系列视频大数据文摘字幕组会持续跟进,陆续汉化推出喔!
https://github.com/llSourcell/The_Math_of_Intelligence
https://github.com/llSourcell/Second_Order_Optimization_Newtons_Method
本期视频时长11分钟,来不及看视频的小伙伴,可以先拉到视频下方看文字部分。
嗨!大家好!我是 Siraj。今天我们来聊一聊优化问题!世界上有成千上万种语言,每种语言在传情达意方面都有其各自的特点,但是有一门语言是全人类共通的,不论你来自哪里。
这就是数学,不论你的文化你的年龄如何,你都能理解这门数字的语言。是它将我们从空间和时间上联系起来。跟其他语言一样,数学也是熟能生巧,但有一点不同的是,数学语言运用得越熟练,在做其他想做的事时你就越游刃有余。

生活中处处有数学,只是一定程度上大多数人都没意识到。我们可以将事物都看成一组变量、看作矩阵,并且这些变量间存在联系。在数学里面,我们把这种联系称之为函数,我们就是用这种方法表达一组模式 一种映射关系,以及多个变量之间的关系。
不论我们用什么机器学习模型,也不论我们用什么数据库,机器学习的目的都在于优化目标,这样做我们就是在准确地估算函数。优化过程通过不断迭代,帮我们发现数据背后的函数。
上周我们介绍了一种较为流行的优化方法,梯度下降法,可以把它分为5个步骤——
1.首先,我们定义某个机器学习模型。该模型具有一组初始权值。箭头所示数值作为模型所表示函数的系数,表格为输入数据与输出预测之间的映射,这些值都是不成熟的预测值。我们不知道实际值应该是多少,但我们正设法找出最优解。
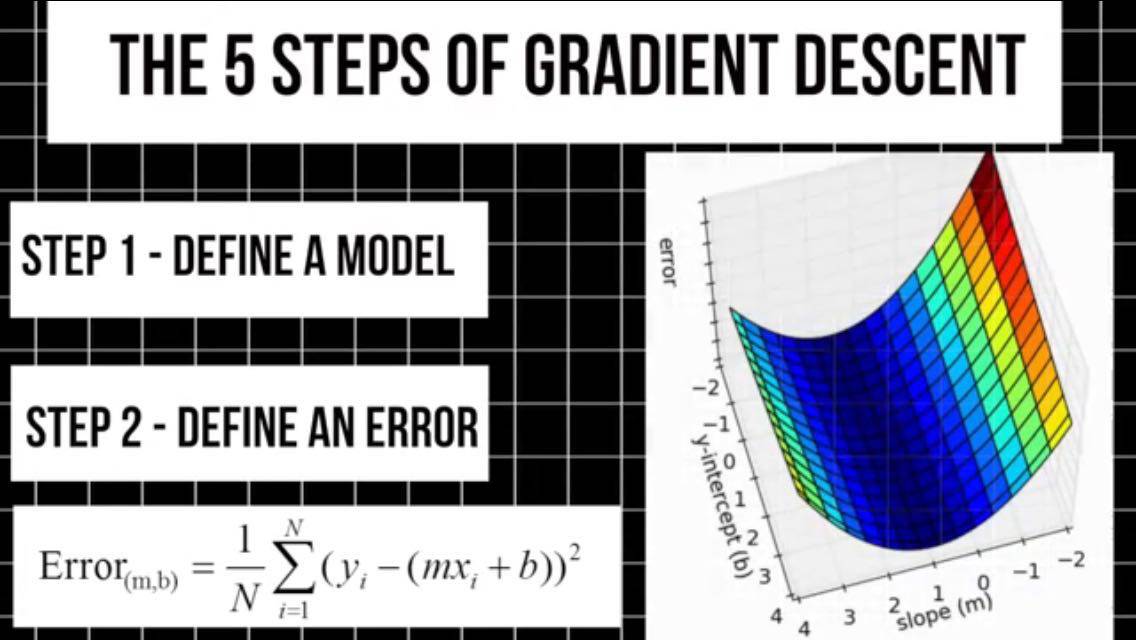
2.我们将定义一个误差函数,绘制一张关系图,表示函数中所有可能的误差值和所有可能的权重值之间的关系。从图上我们可以看到一个最低谷,即最小值。
3.我们利用误差函数帮助计算个权值的偏导,从而得出梯度。梯度表示误差变化,这种变化是由权值,从原始值变化很小的值后引起的。
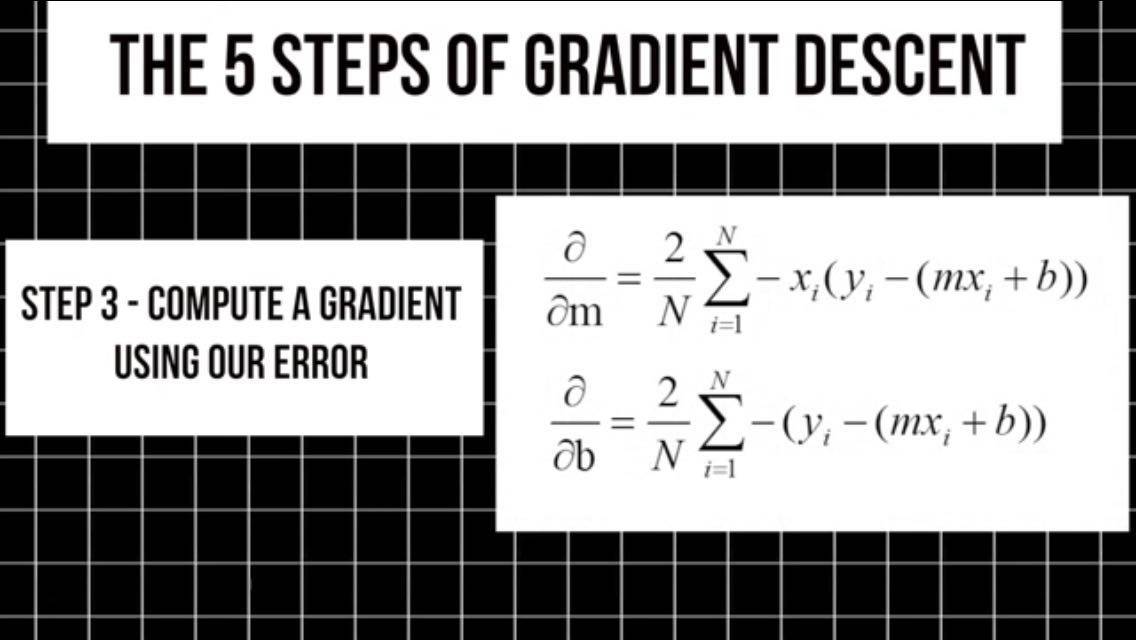
4.我们用梯度变化曲线来定向更新权值,以使误差最小化。通过迭代,逐步接近函数的最小值。
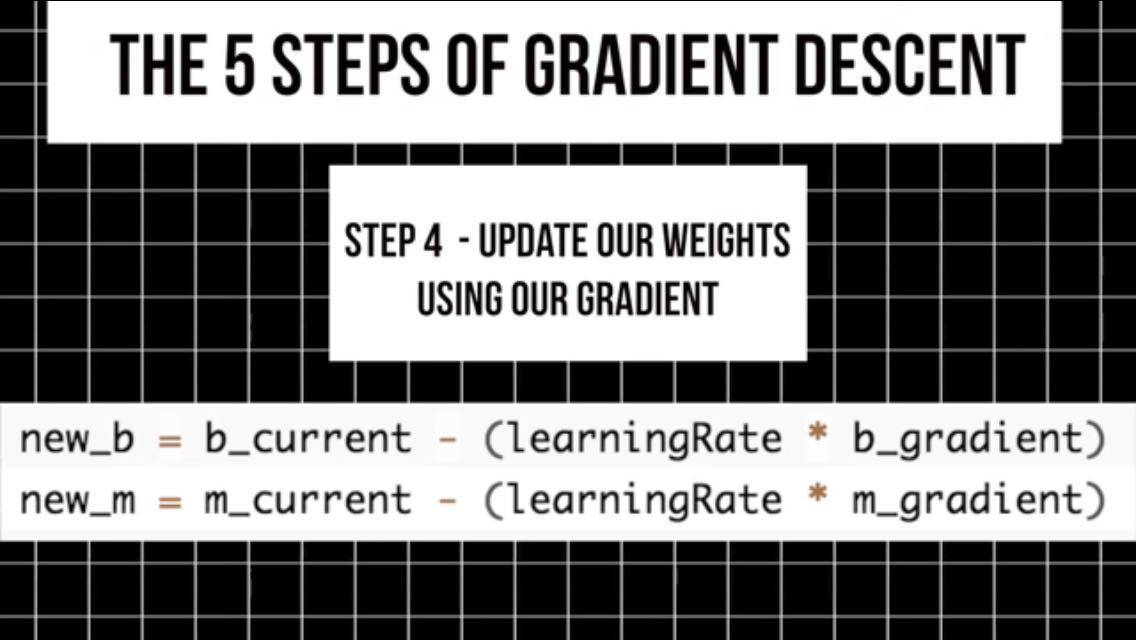
5.在梯度曲线负方向上,重复这一步骤,接近最小值后我们也就得到了所选模型的最佳权值。此时梯度为0,这时该模型就能对输入数据做出预测。
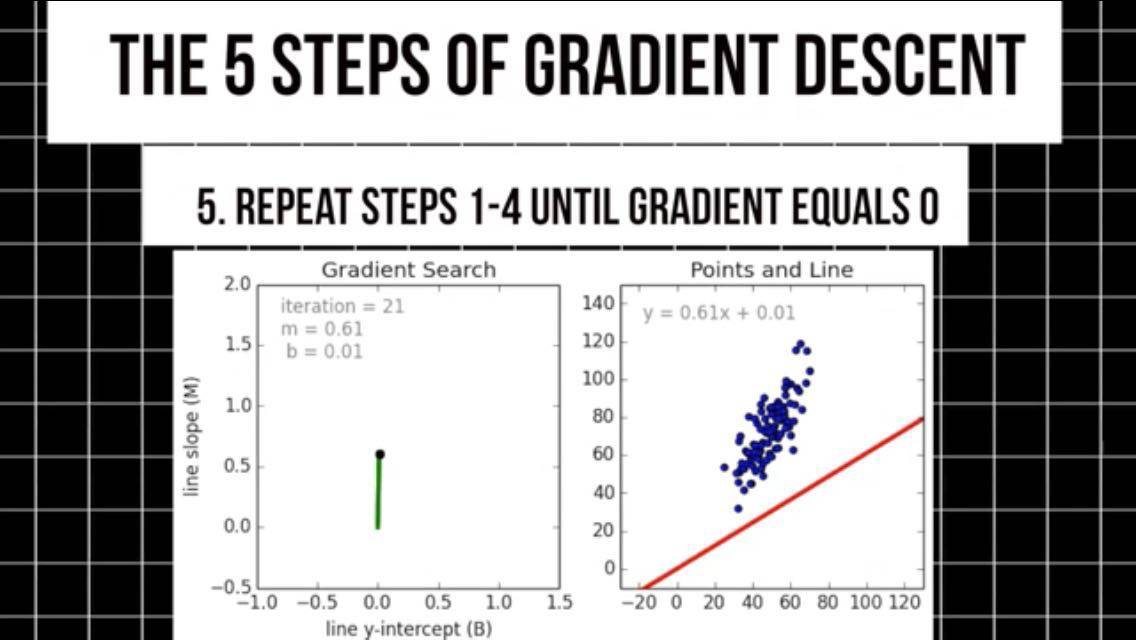
这些数据可以是模型从没用过的,大多数优化问题都能通过梯度下降法及其衍生方法来解决。它们都属于一阶优化方法,之所以称之为一阶,是因为我们只需要计算一阶导数。
还有一类方法,不过它们没有被广泛使用,我们称之为二阶优化法。这类方法要求我们计算二阶导数。一阶导数告诉我们,函数在某一点上是趋于增加还是减少。二阶导数则告诉我们,一阶导数的增减情况。
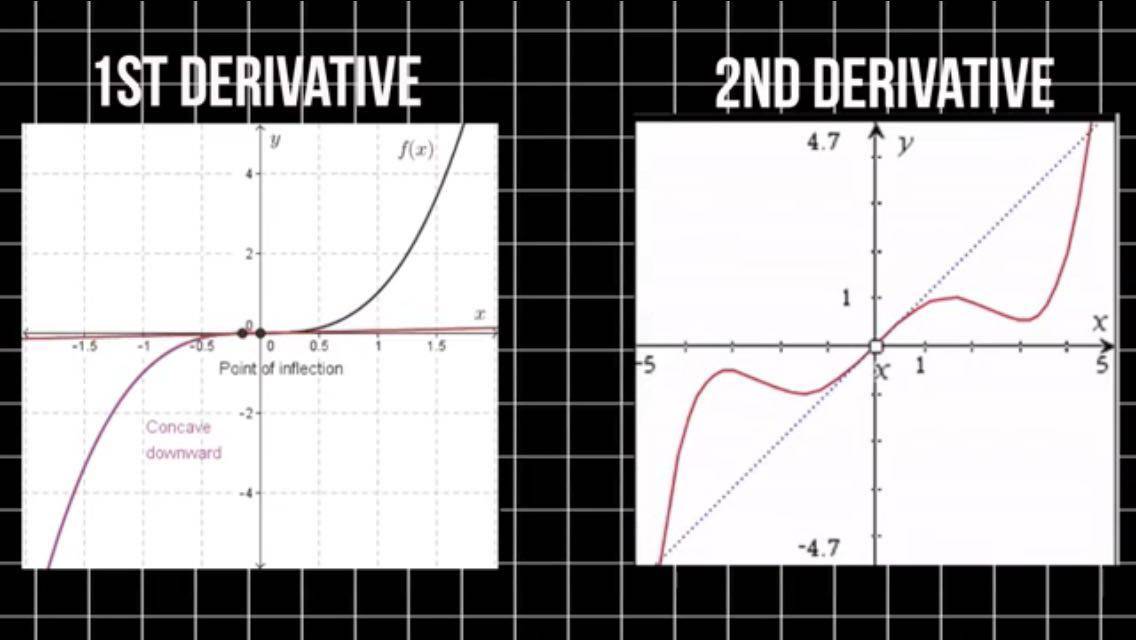
通过一阶优化法,我们可以得到一条经过误差曲面上某一点的切线。而通过二阶法则可以得到一个二次曲面,该曲面与误差曲面的曲率相吻合。
二阶法的优点就在于,它们不忽略误差曲面的曲率。而且就逐步迭代的表现来看,二阶法是更好的选择,让我们来看一种流行的二阶优化方法,叫作牛顿法。就是以发明了微积分的那个家伙命名的,他叫作什么呢?嘿嘿,你懂的!
实际上,牛顿法有两个版本。第一个版本是找出某个多项式的根,也就是图上所有与x轴相交的这些点。所以,如果你抛出一个球并记录它的轨迹,求出方程的根,就会知道球落地的确切时间。
第二个版本是优化法,也是我们在机器学习中用到的方法。
让我们先写写求根版的代码,形成一些基本的直观感觉。譬如说我们有一个函数f(x)和某个猜测的初始解。根据牛顿法,我们要先得出切线在那一猜测点上的斜率,然后求出切线与X轴的交点。

我们用这个交点找到原始函数的映射点,然后我们重复之前的步骤。这一次,我们用得到的映射点作为初始值。
我们不断迭代上面的步骤,直到得出一个不超过某个阈值的x值,这便是牛顿法中的寻根法。
我们利用此方法求出函数在何处为零。但是在最优化法中,我们要找出使函数的导数为零的值,也就是其最小值。
总的来说,只要给定一个随机的初始位置,我们就能构建一个目标函数的二次近似值,该近似值与那一点上的一阶和二阶导数相匹配。然后我们求出这个二次函数的最小值,而非原始函数的最小值;再然后我们用这个二次函数的最小值,作为下一步的初始位置。
然后重复之前的步骤。
那让我们来看两个牛顿法最优化的例子。一个是一维的,一个是二维的。
在第一个例子中,我们有一个一元函数,我们可以用泰勒级数展开公式,得到初始位置的二次近似函数;三阶或更高阶的项我们不予考虑。泰勒级数是一种函数的表示方法,这种函数表示项的无穷和。这些相加的项,通过该函数在某一点的导数值求得。
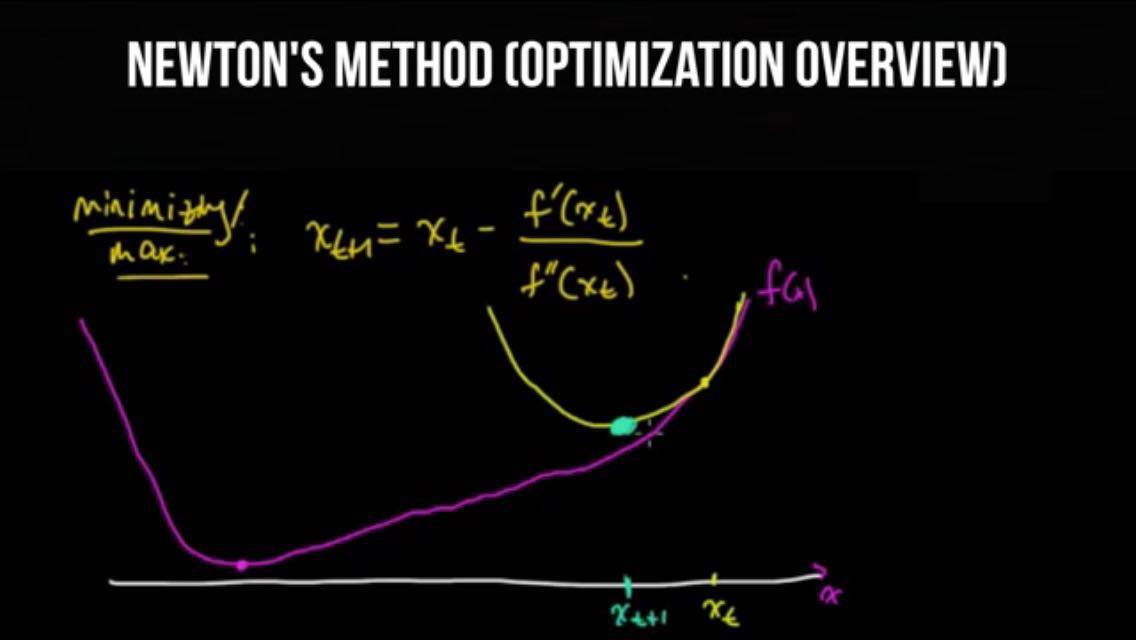
泰勒级数是一位英国数学家发明的,他的名字是布鲁克·泰勒·斯威夫特。然后我们计算初始x点的二阶泰勒级数,并计算出它的最小值。这是通过求出一阶导数和二阶导数,并使它们为零实现的,为了找到最小的x值,我们对这个过程进行迭代。
在第二例子中,我们有一个多元函数,我们可以用之前同样的方法计算最小值。但是有两点不同,我们将一阶导数替换成梯度,将二阶导数替换成海森矩阵,海森矩阵是一个标量的二阶偏导数的矩阵,用来描述多元函数的局部曲率。

导数可以帮助我们计算梯度,而梯度我们可以用雅可比矩阵表示,以此来进行一阶最优化。我们用海森矩阵进行二阶最优化,这些就是5个微积分导数算子中的4个,它们便是我们用数值来组织和表示变化的方法,那么,应该在何时使用二阶法呢?
通常一阶方法的计算量和耗时比较少,当计算大型数据集时一阶收敛非常快,当二阶导数已知并且很容易计算的时候,二阶方法会更快。
但是二阶导数通常很难算,需要极大的计算量。
在某些问题上,梯度下降法会卡住,尤其是在鞍点附近的低收敛性路径上,但是用二阶方法就没有这个麻烦了。
针对你遇到的具体问题,试用不同的优化技巧,才是解决问题的最佳办法,有几个关键点需要记住:
上周代码挑战的获胜者是 Alberto Garces!Alberto 利用梯度下降法找到了最优曲线,他的 Jupyter notebook 无敌详细!光读他写的笔记你都能学会梯度下降法!干的真漂亮!这就是一周代码奇才 Alberto!
第二名是 Ivan Gusev!他从零开始编写代码,将梯度下降法应用于任意阶多项。
本周的挑战是——从头编写代码实现牛顿最优化法!具体详见README。
(https://github.com/llSourcell/Second_Order_Optimization_Newtons_Method)
将你的 GitHub 链接贴在评论中,下周将会公布新一轮的获胜者!如果你想看到更多关于编程的视频,请订阅我。
现在我要去发明第六种导数算子啦!
感谢观赏!















