我们每天睡觉亲密接触的被褥,它的卫生状况值得重视,偶尔就要把被套拆下来洗一洗,洗完再套上去。但这不是个顺当的活计,尽管有系绳,但固定还是相当困难,手艺不好的,实在是难以把它弄得服服帖帖,总是会有些褶皱。这时候难免萌生出偷懒的想法,懒得把被套拉链拉开然后把内芯塞进去了,就随便用被套把内芯当粽子捆了,反正严格来说,的确也是用被套把内芯“套住了”,被套也完成了自身的责任:把内芯的每一处都“挡住”,不让睡觉的人把内芯弄脏。可惜被套一般没有弹性不能延伸,包起来的“粽子”实用面积实在太小,否则这也不失为一个好办法。
无论是正常的还是包粽子的方法,我们都可以说,被套把内芯“覆盖”了。最完美的当然是从头到尾平整光滑的覆盖,内芯上每个地方都被一层被套覆盖;稍差一些,有点皱褶的话,皱褶的地方就会有至少三层被套覆盖着内芯的同一个地方,而且还会有一些“分支点”,皱褶在这些点上开始,又在这些点上终结。如果是包粽子的话,那就不好说了,不过可以肯定的是,内芯上每个点至少有两层被套覆盖。
在数学家眼中,被套可以看成一个球面:假设被套有弹性,那么在里边装一个气球,再把气球吹起来,被套自然会鼓起来变成球面。同样,内芯也可以看成一个球面。如果我们先在内芯放一个气球,然后把内芯和覆盖它的被套缝起来,不让它们移位,最后将气球吹起来,那么我们就得到了被套这个球面对内芯这个球面的一个覆盖。这样的覆盖变化多端,可以是平滑的,也可以有皱褶,在每一点处,覆盖可以是单薄的,也可以是多重的。
把这些直观印象翻译成数学概念,这是数学家们的拿手好戏。球面之间的覆盖,用数学术语来说,就是从一个球面(被套)到另一个球面(内芯)的连续满射函数 ,如果x是被套上的一点,那么
,如果x是被套上的一点,那么 就是内芯上被x这一点覆盖的点。我们要求函数是连续的,因为我们不想把被套扯坏,所以要求被套上的一小块“保护”的也是内芯上的一小块,而不是“分隔异地”的两块;我们要求函数是满射,因为我们希望保护内芯不被弄脏,所以要求内芯上的每一点都有被套保护。当然,数学毕竟是数学,比现实要更天马行空一些。现实中的被套不能穿过自身,而数学中的覆盖则可以。正因为如此,在数学中我们可以把覆盖的皱褶“抚平”,只留下一个个孤立的分支点,这在现实中是不可能的。而我们要求除了分支点以外,球面上的其他点被覆盖的次数都相同,这个次数又被称为球面覆盖的次数。
就是内芯上被x这一点覆盖的点。我们要求函数是连续的,因为我们不想把被套扯坏,所以要求被套上的一小块“保护”的也是内芯上的一小块,而不是“分隔异地”的两块;我们要求函数是满射,因为我们希望保护内芯不被弄脏,所以要求内芯上的每一点都有被套保护。当然,数学毕竟是数学,比现实要更天马行空一些。现实中的被套不能穿过自身,而数学中的覆盖则可以。正因为如此,在数学中我们可以把覆盖的皱褶“抚平”,只留下一个个孤立的分支点,这在现实中是不可能的。而我们要求除了分支点以外,球面上的其他点被覆盖的次数都相同,这个次数又被称为球面覆盖的次数。
http://v.youku.com/v_show/id_XMTc0NDY4NTUxMg==.html
视频原作者:Dugan Hammock,他的Youtube频道上有更多关于曲面的精美视频。
然而,这些东西跟多项式又有什么关系呢?
对于数学家来说,关系非常大。因为他们知道,复数组成的复平面,差不多就是一个球面。有一种叫“球极平面投影”的方法,可以将复平面转化为只缺一个点的球面。而如果我们将“无穷大”也加到复平面里,就能把球面缺的点补上,得到的就是所谓的“黎曼球面”。而黎曼球面上的有理函数,也就是两个多项式的商,实际上就是一个球面覆盖。通过研究球面覆盖的性质,数学家们就能间接得知对应的有理函数的性质。

我们接下来考虑有理函数给出的球面覆盖。球面覆盖的许多性质都被它的分支点所决定,因为分支点以外的地方都非常平滑,到了乏善可陈的地步,而分支点正是曲面“叠起来”的地方,自然包含了我们想要的性质。我们可以说,球面覆盖的分支点越少,它就越简单。
那么,对于有理函数来说,怎么寻找它的分支点呢?还是拿被套作例子。当被套有皱褶时,皱褶的部分实际上是三层被套覆盖同一点,但同样应该属于皱褶一部分的分支点上,却只有一层被套。也就是说,分支点覆盖的层数比正常的要少一些。如此类推,对于函数
我们接下来考虑有理函数给出的球面覆盖。球面覆盖的许多性质都被它的分支点所决定,因为分支点以外的地方都非常平滑,到了乏善可陈的地步,而分支点正是曲面“叠起来”的地方,自然包含了我们想要的性质。我们可以说,球面覆盖的分支点越少,它就越简单。
那么,对于有理函数来说,怎么寻找它的分支点呢?还是拿被套作例子。当被套有皱褶时,皱褶的部分实际上是三层被套覆盖同一点,但同样应该属于皱褶一部分的分支点上,却只有一层被套。也就是说,分支点覆盖的层数比正常的要少一些。如此类推,对于函数 引出的球面覆盖来说,假设它的覆盖次数是d,那么说某个点a是分支点,就相当于说
引出的球面覆盖来说,假设它的覆盖次数是d,那么说某个点a是分支点,就相当于说 这个方程的解值少于d个,因为这个方程的每一个解其实都是“被套”上覆盖a的一点。换句话说,a是分支点当且仅当
这个方程的解值少于d个,因为这个方程的每一个解其实都是“被套”上覆盖a的一点。换句话说,a是分支点当且仅当
有重根。
举个实际的例子。我们考虑函数

显然方程 有三次重根x=1,所以0是它的一个分支点;而稍微令人意想不到的是,如果我们将它减去1,就会得到
有三次重根x=1,所以0是它的一个分支点;而稍微令人意想不到的是,如果我们将它减去1,就会得到

 可以看出来,方程
可以看出来,方程
 有两个二次重根,分别是二次方程
有两个二次重根,分别是二次方程
 的两个解,所以1也是一个分支点。最后还有一个分支点比较难想像,那就是无穷远点,因为当x趋向无穷或者0时,
的两个解,所以1也是一个分支点。最后还有一个分支点比较难想像,那就是无穷远点,因为当x趋向无穷或者0时,
 也趋向于无穷,所以无穷远点也是一个分支点。可以证明,这个函数再也没有别的分支点了。
也趋向于无穷,所以无穷远点也是一个分支点。可以证明,这个函数再也没有别的分支点了。
最简单的球面覆盖,一个分支点都没有,就是最标准的把内芯塞进被套里的方法。球面到自身的恒等映射 就是这样的一个例子。可以证明,不存在只有一个分支点的球面覆盖,也就是说,接下来第二简单的情况就是拥有两个分支点的球面覆盖。可以证明,所有拥有两个分支点的球面覆盖,都可以利用适当的变换来“拉扯”变形到
就是这样的一个例子。可以证明,不存在只有一个分支点的球面覆盖,也就是说,接下来第二简单的情况就是拥有两个分支点的球面覆盖。可以证明,所有拥有两个分支点的球面覆盖,都可以利用适当的变换来“拉扯”变形到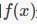
是多项式的情况。
数学家们接下来要研究的,自然就是拥有三个分支点的球面覆盖。利用有名的莫比乌斯变换

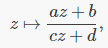
我们可以将三个分支点分别移动到0、1和无穷远点(∞),而莫比乌斯变换不会改变球面覆盖的本质。所以说,我们只需要研究分支点分别在0、1和∞的球面覆盖,而能产生这样的球面覆盖的函数又叫别雷函数(Belyi function,正确地说是球面上的特殊情况),它的名字来源于20世纪的俄罗斯数学家别雷(G. V. Belyi)。但实际上,别雷并不是第一个研究别雷函数的人。早在19世纪末,大数学家菲利克斯·克莱因(Felix Klein)就已经利用别雷函数构造过一些特殊的球面覆盖(更精确地说,是单值群为有限单群PSL(2,11)的球面覆盖,它是一个11次覆盖)
http://v.youku.com/v_show/id_XMTc3MDExNzY0OA==.html
节选自《Möbius Transformations Revealed》,原作者为Douglas Arnold和Jonathan Rogness,完整版本可在视频页面找到。
但球面覆盖毕竟太抽象,即使是数学家,不借助适当的工具也难以“脑补”某个具体函数引出的覆盖,而对于一般人来说,光是球面可以穿过自身这一点就足够喝一壶的了,更不要说想像那些“折痕”都集中在几个分支点上的高次覆盖。要研究这些球面覆盖,似乎是难于登天。
但数学家却说,三个分支点的球面覆盖,其实简单得连小朋友都能画出来。
小朋友的涂鸦
要讨论别雷函数,就要对球面覆盖和复分析有些更深入的了解。接下来的内容可能有一点抽象,如果实在不适应,可以跳过,直接看本节最后的结论。
我们要研究的,是分支点分别在0、1和∞的球面覆盖,或者说某个别雷函数
 。既然球面覆盖的所有玄妙之处都蕴藏在分支点里,那么肯定要抓住这些分支点来研究。我们之前考虑过一个例子:
。既然球面覆盖的所有玄妙之处都蕴藏在分支点里,那么肯定要抓住这些分支点来研究。我们之前考虑过一个例子:


它是一个别雷函数,对应着一个球面覆盖。用一点点复分析的知识(代数基本定理),容易知道除去一些特殊情况外,对于任意的常数a,
 处有一个分支点,因为x=1是这个方程的三重根,但它还有另一个根x=9,也就是说,0这个分支点实际上对应两个不同的点:三重根x=1和单根9.
处有一个分支点,因为x=1是这个方程的三重根,但它还有另一个根x=9,也就是说,0这个分支点实际上对应两个不同的点:三重根x=1和单根9.
同理,1这个分支点同样对应两个不同的点,两个都是双重根。我们能看到,两个分支点的分支方式不同,但既然它们从属于同一个球面覆盖,那么之间必然有某种联系。怎么样才能考察它们之间的联系呢?
办法很简单:直接把两个点连起来就好了。也就是说,我们希望观察这两个分支点的每一层覆盖分支之间是如何连接起来的。
更具体地说,因为球面覆盖就是一个球面覆盖着另一个球面,只要在被覆盖的球面上连结0和1两个点,在得到的线段上涂上极浓重的颜料,等到颜料渗透到覆盖的每一层之后,再将覆盖展开,得到的就是球面上的一幅图。用术语来说,就是研究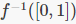 。那么,我们得到的图像会是怎么样的呢?还是用刚才的函数来举例,我们得到的图像如下:
。那么,我们得到的图像会是怎么样的呢?还是用刚才的函数来举例,我们得到的图像如下:

在上图中,黑点代表0对应的点 ,而白点代表1对应的点
,而白点代表1对应的点 和
和 。因为这个球面覆盖的次数是4,所以线段[0,1]上的点实际上被覆盖了四次,也就是说,当覆盖展开之后,我们将会看到四段曲线(四条边),它们连接着0对应的两个点
。因为这个球面覆盖的次数是4,所以线段[0,1]上的点实际上被覆盖了四次,也就是说,当覆盖展开之后,我们将会看到四段曲线(四条边),它们连接着0对应的两个点 ,还有1对应的两个点
,还有1对应的两个点 三重根x=1上连着三条边,单根上连着三条边,单根x=9只有一条,而两个双重根
三重根x=1上连着三条边,单根上连着三条边,单根x=9只有一条,而两个双重根 各自连接两条边。函数在
各自连接两条边。函数在 两个点上发散,而这个图恰好又有两个面,外部的面对应
两个点上发散,而这个图恰好又有两个面,外部的面对应 ,而内部的面对应x=0,而这些面的度数(也就是边界的长度)与函数在对应点上发散的度数相关。也就是说,单单从这幅图像里,我们就能读出函数本身的许多代数性质。如果把顶点连接的边的数目称为顶点的度数的话,图像性质与代数性质的对应可以归纳成下面的列表:
,而内部的面对应x=0,而这些面的度数(也就是边界的长度)与函数在对应点上发散的度数相关。也就是说,单单从这幅图像里,我们就能读出函数本身的许多代数性质。如果把顶点连接的边的数目称为顶点的度数的话,图像性质与代数性质的对应可以归纳成下面的列表:
| 别雷函数 | 平面二部地图 |
|---|
| 覆盖的次数 | 边的条数 |
| 0处的分支点 | 黑色顶点 |
| 1处的分支点 | 白色顶点 |
| ∞处的分支点 | 面 |
| 0处和1处分支点的重数 | 顶点的度数 |
| ∞处分支点的重数 | 面的度数的一半
|
实际上,对于所有的别雷函数,展开对应的球面覆盖后,线段[0,1]的图像总是包含着我们想要的很多代数性质:边的数目对应着覆盖的次数,黑点对应着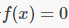 的分支,白点对应着
的分支,白点对应着
的分支,面对应着无穷大的分支,而每一个点和每一个面连接多少条边,都对应着球面覆盖在对应的分支上“折叠”起来的方法。
那么,别雷函数对应的这些图像,到底又是什么呢?
我们先忽略那些点和线的具体位置和形状,而只关注它们是如何在球面上连结起来的。用数学术语来说,就是先忽略它们的几何性质,而专注于它们的组合性质。首先,因为每条边实际上都来自线段[0,1],所以它们连结的必定是一个对应着
 的黑点和一个对应着
的黑点和一个对应着 的白点。也就是说,别雷函数对应的图像,实际上可以抽象成一个二部图,这类图的顶点,一黑一白,而每条边的两端恰好是一黑一白两个顶点。但这些图像跟一般所说的二部图不完全一样。在数学中,一个图就是一堆顶点加上连结顶点的一些边,但连结同一个顶点的边之间并没有什么特别的关系。但别雷函数对应的图像实际上是一个画在了球面上的图,所以连结同一个顶点的边会在围绕在顶点周围,这就给它们赋予了顺序关系。这样画在了球面(或者别的封闭曲面)上的图,又叫组合地图。而别雷函数对应的图像,正式的名称是平面上的二部地图。在这里,组合地图即使画歪了一点,只要保持顶点、边以及边之间的关系,还算是同一个地图。
的白点。也就是说,别雷函数对应的图像,实际上可以抽象成一个二部图,这类图的顶点,一黑一白,而每条边的两端恰好是一黑一白两个顶点。但这些图像跟一般所说的二部图不完全一样。在数学中,一个图就是一堆顶点加上连结顶点的一些边,但连结同一个顶点的边之间并没有什么特别的关系。但别雷函数对应的图像实际上是一个画在了球面上的图,所以连结同一个顶点的边会在围绕在顶点周围,这就给它们赋予了顺序关系。这样画在了球面(或者别的封闭曲面)上的图,又叫组合地图。而别雷函数对应的图像,正式的名称是平面上的二部地图。在这里,组合地图即使画歪了一点,只要保持顶点、边以及边之间的关系,还算是同一个地图。

现在我们知道,每个别雷函数都对应着一个平面上的二部地图,那么是不是所有这样的地图都对应着一个别雷函数呢?事实上,利用一些复分析方面的知识,可以证明别雷函数与球面上的二部地图有着一一对应的关系。不仅如此,我们还能把这些别雷函数限定为系数是代数数的分式(代数数就是整系数多项式方程的解)。这实际上就是别雷的贡献:他在1979年证明了,对于一大类重要函数(所谓的“光滑代数曲线”),它们(的适当的等价类)与别雷函数引出的球面覆盖有着一一对应的关系。这些“光滑代数曲线”可以粗略理解为分支点只有0、1和∞,系数是代数数的分式。也就是说,如果我们要找分支点满足某些条件的分式,只需要看看根据这些条件能不能在平面上画出一个二部地图就可以了。
总结一下:三个分支点的球面覆盖,等价于所谓的“平面上的二部地图”,在这个地图上有黑色和白色两种顶点,而每条边都连接一黑一白两个顶点,从而把所有顶点连成一片。而球面覆盖的许多性质,都能反映在地图上的顶点、边和面上。别雷证明了,“光滑代数曲线”(大概就是某一类系数是代数数的分式)与三个分支点的球面覆盖有着一一对应的关系。所以,要寻找分支点满足某些条件的分式,只需要看看能不能画出满足对应条件的二部地图。而任意一个二部地图,哪怕是小朋友的涂鸦作品,也必然存在对应的分式,它的球面覆盖展开之后就是这个二部地图。

说了半天,云里雾里的,这又有什么意义?














