Support Vector Machines (SVMs) are a popular machine learning
algorithm with lots of usages and I learned something quite amazing
about them. But first let me tell you what SVMs do.
Imagine we have data points of two different classes:
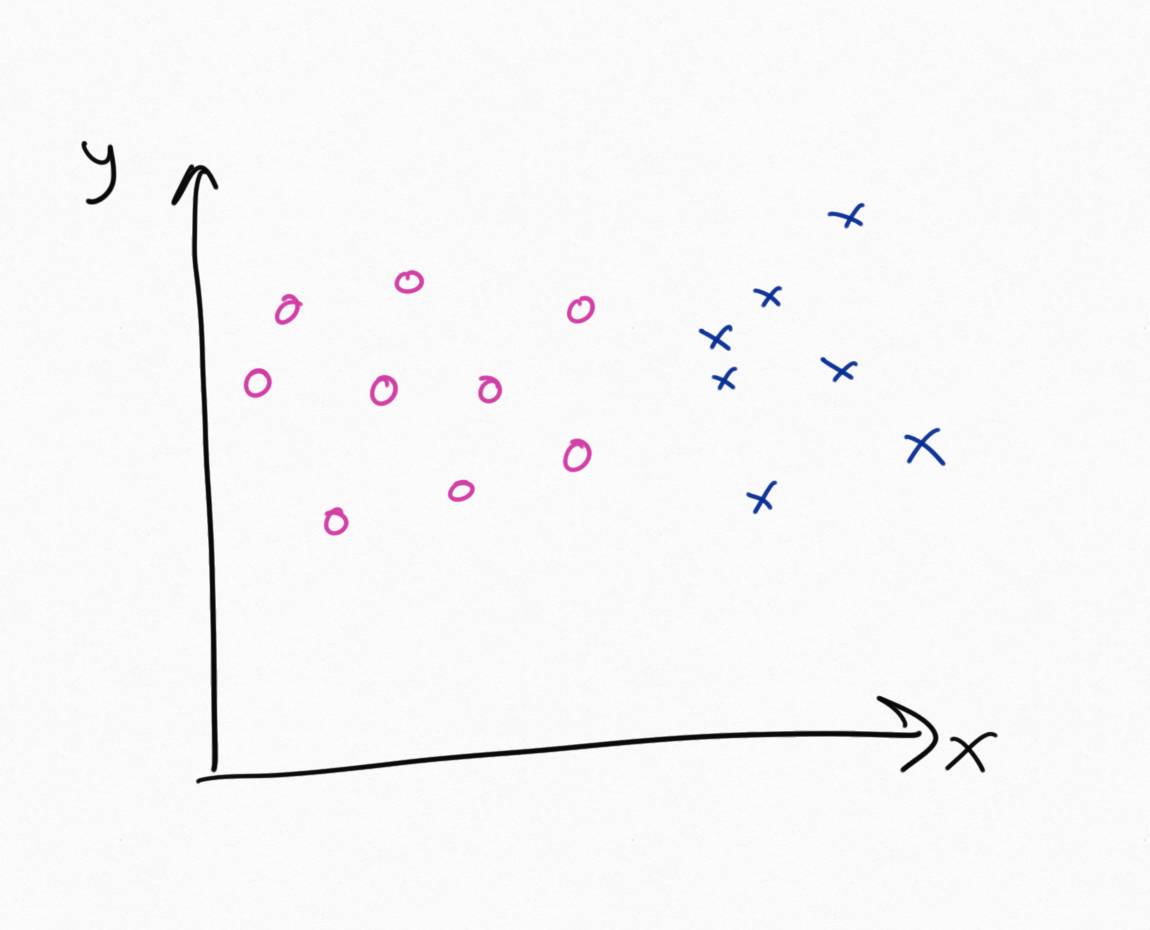
A support vector machine can take that data as input and find a line
that separates it. We call this line the decision boundary. But there
are many separating lines, which one is the best? SVMs are going to
choose the line that maximises the margin. Margin is the distance
between the separating line and the nearest point of either of the two
classes.
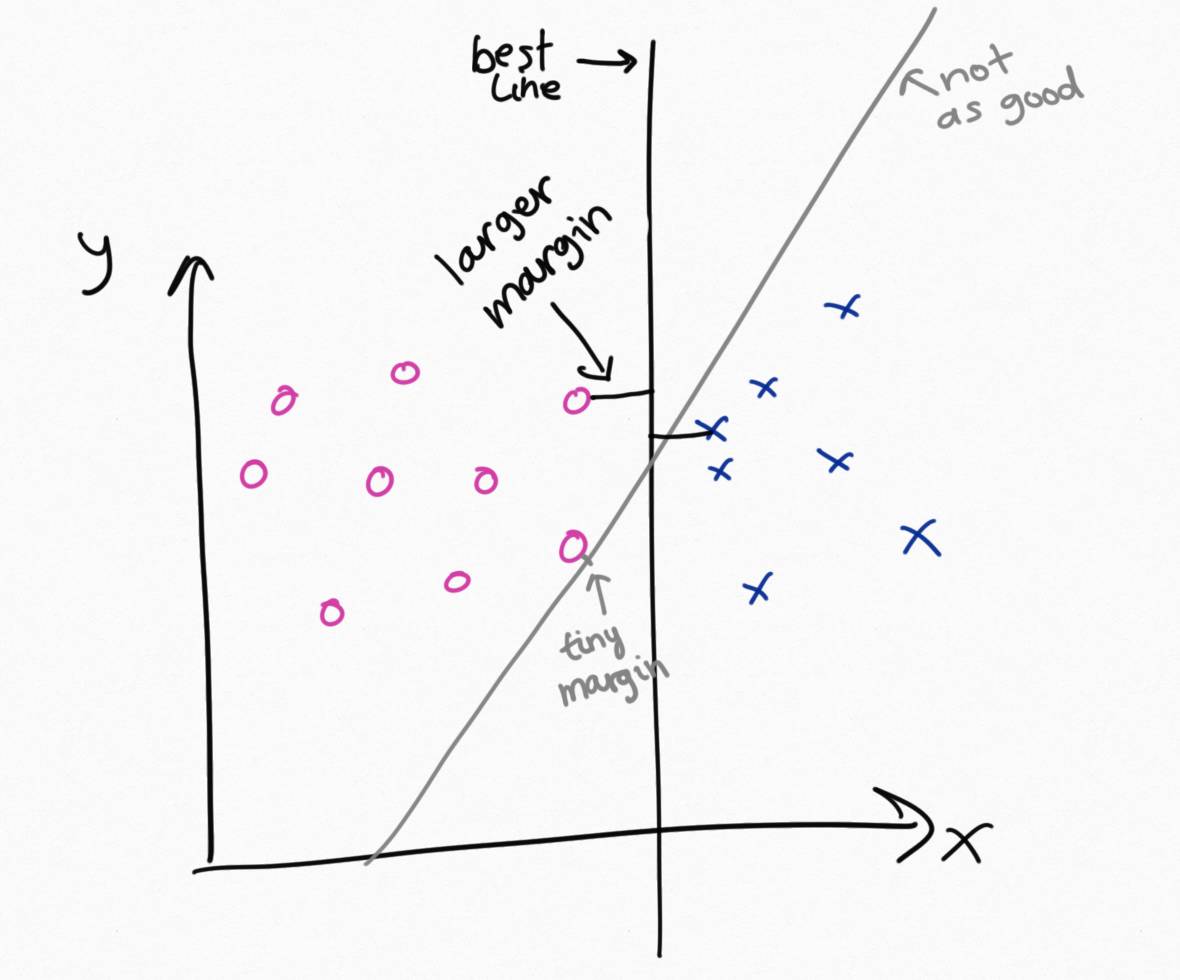
The intuition behind trying to maximise the margin is that a decision
boundary with a smaller margin is more prone to overfitting, while a
larger margin makes the result more robust.
Non-linear data
Now look at this data:
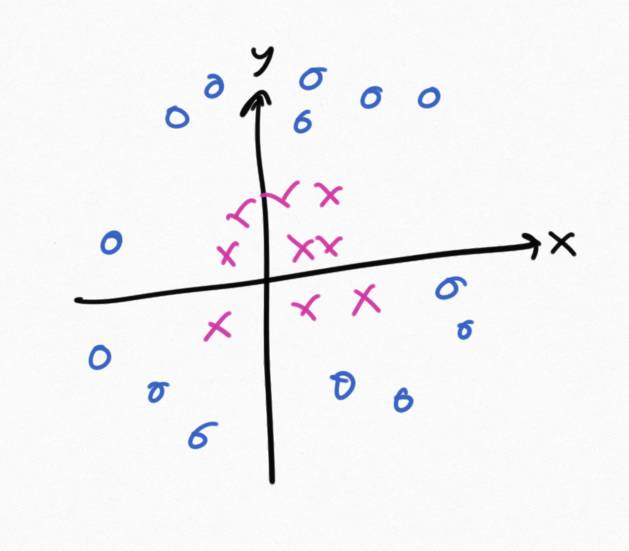
Given what we’ve seen so far we’d think an SVM couldn’t separate this, as there just isn’t a good separating line for this data.
But there’s a trick! It works like this: we’ll add a new feature to the data. So far we had 2 features, x" role="presentation">x and y" role="presentation">y, and we’re gonnna add one more. In this example I’ll conveniently choose a value for the new feature that I know works: x2+y2" role="presentation">x2+y2
So now we have three dimensions and the z" role="presentation">z axis has value x2+y2" role="presentation">x2+y2
. This is equal to the distance of each point from the origin.
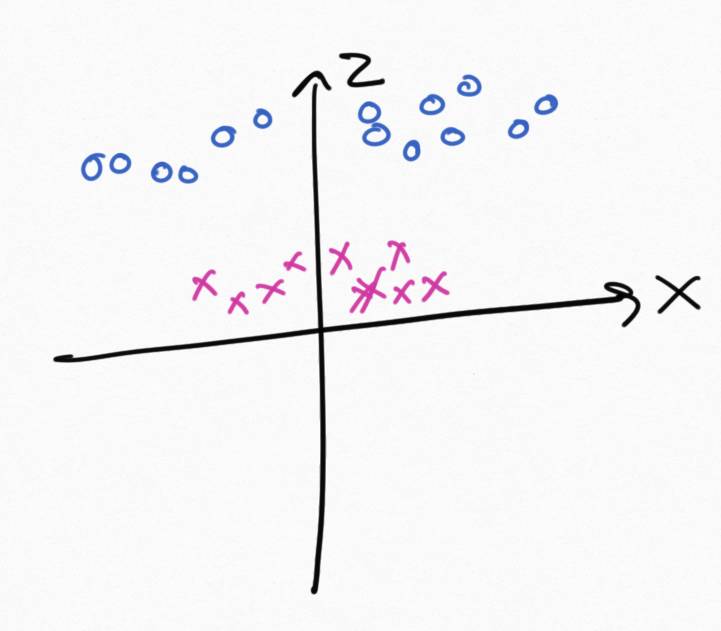
Is this now linearly separable?
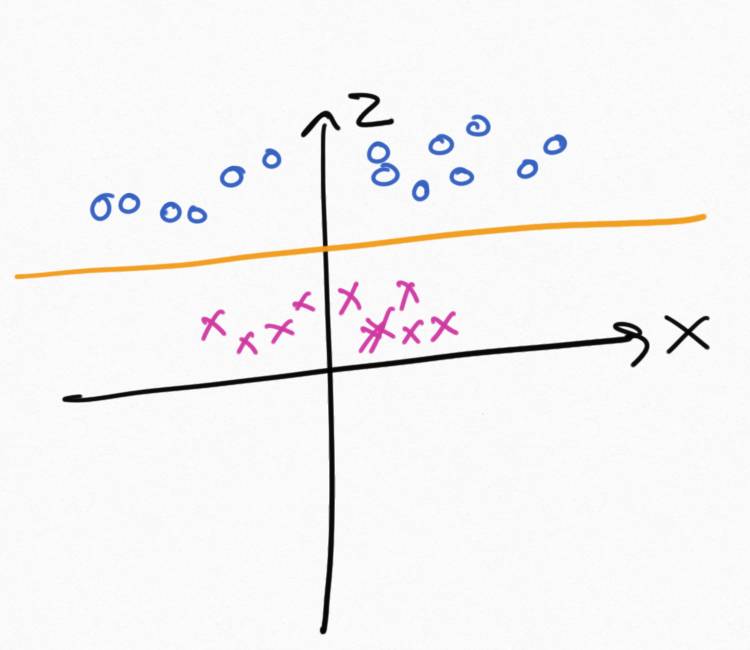
And the answer is yes, there is a hyperplane that can separate the pink from the blue points.
The next step is to take this solution and go back to the original two-dimensional space. Since this line on the z" role="presentation">z axis has an equation of x2+y2=something" role="presentation">x2+y2=something it corresponds to a circle:
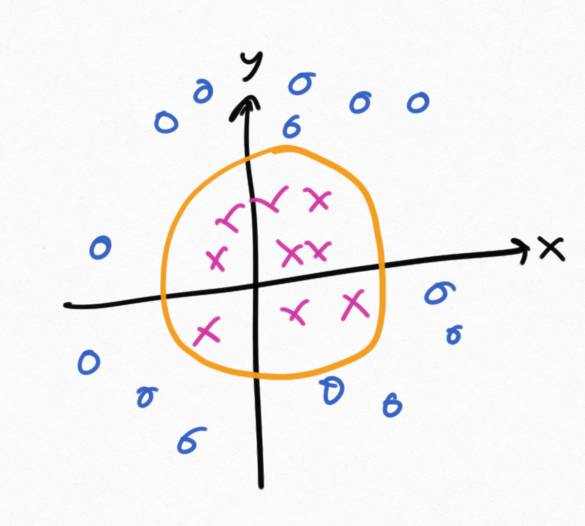
What we did
Here’s what we did:
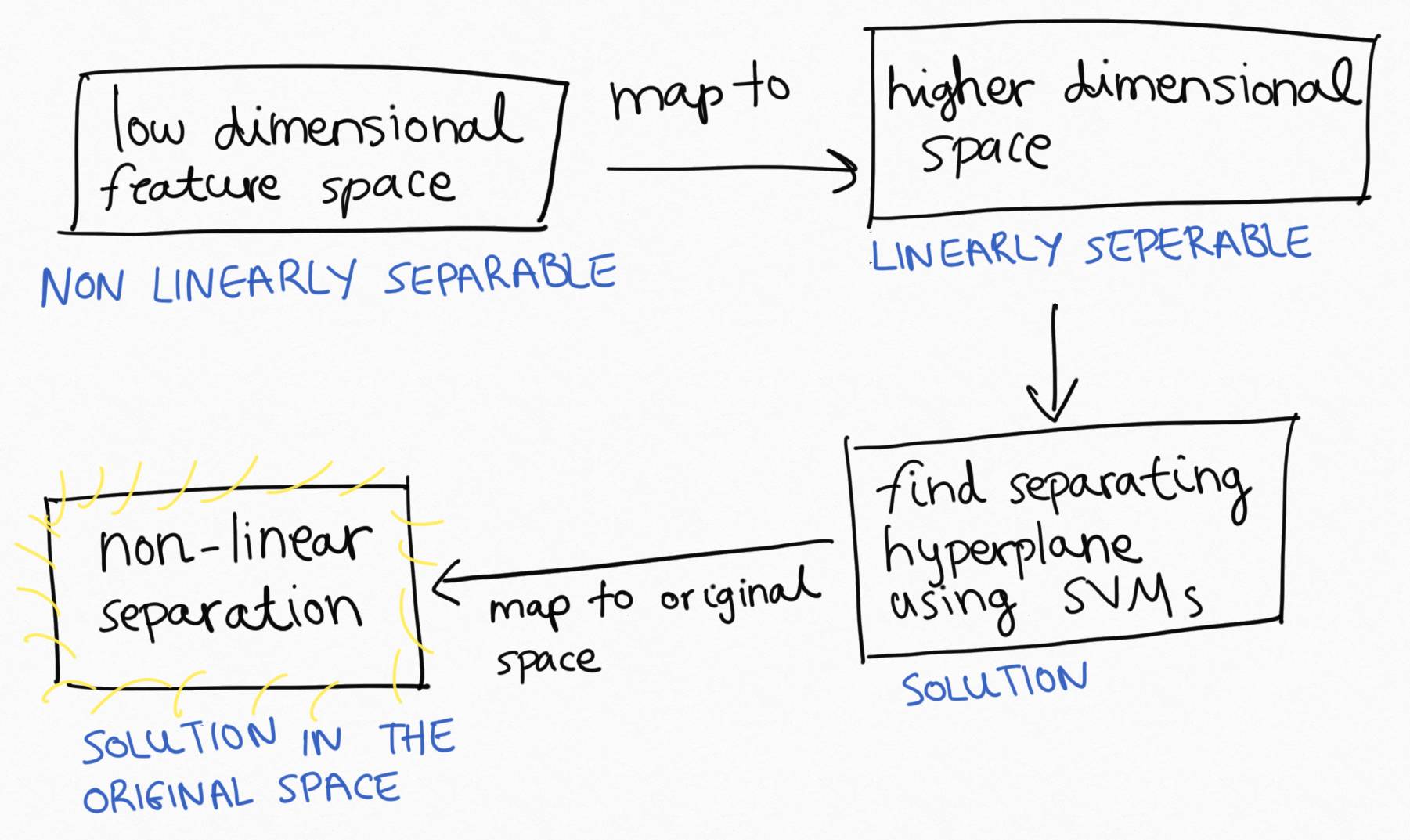
That’s pretty cool!
链接:
https://generalabstractnonsense.com/2017/03/A-quick-look-at-Support-Vector-Machines/
原文链接:
http://weibo.com/1402400261/EBPuQ9ybX?from=page_1005051402400261_profile&wvr=6&mod=weibotime&type=comment#_rnd1490702144628















