我们在数列部分常碰到这样的问题:证明某个复杂数列为等差或者等比数列(简称“两等数列”).比如下面这道题.

首选定义法
从求证出发,我们回顾等比数列的定义:从第2项开始,数列的后一项除以前一项等于同一个不为零的常数,则这个数列为等比数列.
这就是我们证明等比数列的主要办法,也称定义法.即只需证明后项/前项为同一个非零常数即可.

这个方法有什么技术含量呢?
就两点.
1.首先
把后项用前项表示;
2.在化简过程中,
保持前项不变,后项代入.
道理也是显然的,要使得计算结果为常数,必须要出现消项、约分,所以把后项朝前项去靠近,才能最终通过消项、约分得到常数.
根据条件中给定的关系式,代入上式.

结果还真是一个常数,神奇吗?
其实一点也不神奇,只要方法正确,常数是命题者设计好了的,你不用担心.
如何证明分段数列为两等数列?
下面,增加一点难度,看这一道分段形式给出的数列递推式.

请自觉做题3分钟.不要往下看.
你还是忍不住看了,好吧.
分析:首先来理解数列递推式传递的信息.我们用具体的例子来理解它.

我们对数列还是一头雾水,但是有了一些感性的认识.
不管怎样,还是采用定义法来证明.
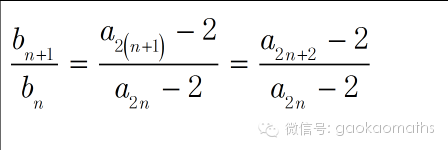
还是采用前面介绍的技巧:
保持前项不变,把后项用前项表示之后再代入.
注意看,分子项和分母项的脚标相差2,我们根据题目所给递推式,可以分两步来.
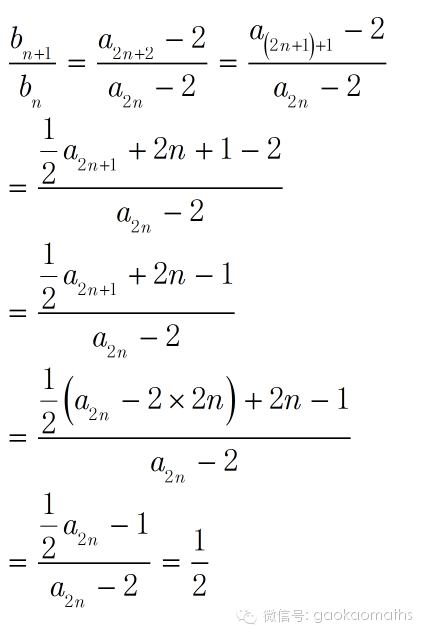
咦!结果又是一个常数.
废话,要不是常数,那就是题目出错了.
正所谓:定义法来真好用,证明等比显奇功.
推荐阅读:
构造函数求最值
上一篇:
含两个绝对值的线性目标函数
--END--
苹果手机用户专属赞赏二维码






