少数派报告
| 理解M值
图片来自
Erik C Baker
下文由
程程_Constance
译自 Erik C Baker 发表的论文《Understanding M Values》,并
基于中国大陆创作共用协议3.0之署名-非商业性使用-相同方式共享(CC BY-NC-SA 3.0)编辑发布,译作权归译者所有
写在前面
似乎从接触技潜
开始
,M Values 和 GF Low, GF High 就成了一组大家耳熟能详却又讲不清楚的热搜词汇。GF Low 和 GF High 更是化身成了各潜水员的迷之高低女友,你越想弄懂她们,就越是似懂非懂。网上曾经流传过很多关于 M 值和高低女友的图解与科普,但大多都是经过演绎的产物。下面这篇《理解 M 值》则是这些演绎的源头,希望能帮到你一点点。

本文略长
一口气读完大概需要20分钟
弄懂大概需要2周
关掉只需要2秒
理解 M 值
原文作者:
Erik C Baker
原文出处:
请点击阅读原文
组织细胞内惰性气体压强的计算、M值,与一系列假想的对照组织间隔一起构成了溶解气体或 “Haldanian” 减压模型的三大要素。广大技术潜水员习惯于使用基于该模型设计的减压软件来制定减压计划以确保自己的潜水安全。对M值的充分理解有助于潜水员在做减压计划时设定恰当的保守系数,并对某一次潜水的不同减压计划作出合理评估,选出最合适的一个。
那么M值到底是什么?“
M值
”这一术语最先是由 Robert D. Workman 在20世纪60年代中期提出的,当时他正在为美国海军试验潜水部队(Navy Experimental Diving Unit,NEDU)进行减压有关的研究。Workman 是一名医生,也是美国海军医疗队的一名上尉。
M值中的M代表的是 “Maximum”,即最大值的意思。
M值被定义为在给定的环境压强下,某一指定对照组织间隔内可承受的(即不会出现明显减压病症状)惰性气体压强的最大值,该值是一个绝对值,而非比值或差值。
各对照组织间隔的M值决定了其内部惰性气体压强与其所处环境压强之间所允许的最大压强差。其它用来表示M值的词汇还有“可承受的超压极限”、“
临界张力值
”和“过饱和极限”。
历史背景
在溶解气体或 “Haldanian” 减压模型中,我们会将每一对照组织间隔内惰性气体压强的计算结果与“上升限制标准”进行比较来制定安全可行的减压计划。
在该模型发展的早期,包括 John S. Haldane 在1908年提出的减压算法在内,“上升限制标准”都是以“过饱和比率”的形式来定义的。
当时,Haldane 发现一个呼吸空气且体内组织细胞在水下33英尺(10米)达到饱和的潜水员可以直接上升至水面而不会获得明显的减压病症状。由于水下33英尺(10米)的环境压强是海平面大气压强的两倍,Haldane 得出结论,
组织细胞可忍受的超压(即过饱和度)与环境压强的最大比率为2:1,该比率应做为潜水员升水时的上升限制标准。
Haldane 采用该比率设计了第一套减压计划表格。在之后的许多年里,一直到20世纪60年代,又有很多其它的过饱和比率被不同的
减压模型研究者提出并被应用到
半饱和周期不同的对照组织间隔中去。美国海军的大多数减压表格都是由过饱和比率计算而来的。
然而,这些由“过饱和比率”计算所得的减压表格似乎存在一些问题,尤其是在潜水员进行深度较深、时间较长的潜水的时候。Robert Workman 于是开始对这些减压模型以及美国海军过去所做的研究进行系统地复查与校对并得出了一些重要的结论。首先,他意识到,
如果我们只考虑空气中的惰性气体(即氮气)分压的话,之前 Haldane 基于空气潜水提出的2:1这一过饱和比率实际上应该为1.58:1。
在当时,人们已经知晓减压病的罪魁祸首并非氧气,而是诸如氮气和氦气那样的惰性气体。在 Workman 复查研究数据的时候,他还发现
过饱和比率并非是一成不变的,不同半饱和周期的组织细胞在不同的深度都有不同的过饱和比率
。数据表明半饱和周期短的组织细胞(即快组织细胞)要比半饱和周期长的组织细胞(即慢组织细胞)可以承受更大的过饱和比率;而且对于所有组织细胞而言,随着潜水深度的增加,其可承受的过饱和比率则在不断减小。
因此,Workman 提出了“M值”的概念,用来代替“过饱和比率”来描述人体各组织细胞在各深度可承受的最大氮分压和氦分压。
接下来,Workman 将这些M值以深度为函数进行了线性映射,他发现该映射是基本符合真实数据的。该线性映射对减压软件的编程至关重要。
Workman 的M值
Workman 对M值的线性映射是溶解气体减压模型发展进行中不可或缺的一步。
他的M值确定了水深产生的压强与每个对照组织间隔内可承受的惰性气体压强成线性关系这一概念。
此概念是当今溶解气体模型的一个重要组成部分,并被各减压建模型的研究者广泛地应用到自己的模型中去。
Workman 使用线性方程的斜截式(即 y=kx+b)表达了M值(如图一)。其中,海平面所对应的M值被称为M
0
(读作M零);方程的斜率被称为△M(读作 delta M),即M值随深度变化而发生的改变。
Bühlmann 的M值
Albert A. Bühlmann 教授于1959年在瑞士苏黎世大学医学院的高压氧生理学实验室开始了减压有关的研究。
Bühlmann
的研究一直持续了30多年,并对减压科学做出了许多重要的贡献。1983年,他以德文出版发行了一本成功的著作 - 《减压,减压疾病》,该书的英文译本也在1984年成功问世。该书是第一次面向大众对潜水减压有关的计算做出非常全面的解释。也正因如此, “
Bühlmann 算法”成为了世界上大多数潜水电脑表和电脑减压软件的计算基础。这本书的另外三个德文版本也分别于1990年,1993年和1995年相继问世。于1995年第4次再版的《减压,减压病》的英文译本也在准备出版发行。
Bühlmann 的减压算法与 Workman 的算法相类似,其中也包含了M值的概念。Bühlmann 的M值也肯定了假想的对照组织间隔内可承受的惰性气体压强与其所处环境压强成线性关系这一概念。
这两种方法的主要区别在于 Workman 的M值是基于深度压强(即压力表读数,且假设潜水员是从海平面开始潜水)所得的,而 Bühlmann 的M值是基于绝对压强(即环境压强,且假设潜水员会进行高海拔潜水)所得的。
当然,这也是情理之中的事情,因为 Workman 当时更关心的是美国海军的潜水活动(大多数都是在海平面以下进行的潜水),而
Bühlmann
研究的潜水则大多数都是在瑞士的高山湖中进行的。
Bühlmann 发表了两组在潜水圈内广为人知的M值。一组是来自1983年出版的
《减压,减压疾病》
一书中的ZH-L12,另一组则是来自该书于1990年再版的
ZH-L16。在这两组名词定义中,ZH 代表 Zürich,即
Bühlmann
的家乡苏黎世;L代表的是
Limit
,即
极限
的意思;12和16则分别代表了用于计算氮气与氦气
M值的
安全系数的对照组织间隔数量。
ZH-L12
一共为12组对照组织间隔计算了12对儿安全系数,这些安全系数均是根据真实减压实验所得。
ZH-L16则是对16组对照组织间隔的安全系数进行了计算,但这些安全系数仅是根据惰性气体的过载量、溶解度及其半饱和周期计算所得,并未经过实验的检测。由于
在后来的实验中
,仅通过数学推导的
ZH-L16
A的安全系数对中组织细胞来说不够保守,
ZH-L16
又被进一步调整为
ZH-L16
B和
ZH-L16
C。其中,
经过改进的ZH-L16
B
更加适用于
静态
减压计划表的设计(即固定深度与时间),而
ZH-
L16C则适用于潜水电脑表在水下进行实时减压计算。
与 Workman 的M值类似,Bühlmann 的M值也是用线性方程的斜截式表达的(如图一)。安全系数a是绝对环境压强为零时
斜截式与Y轴(即给定对照组织间隔内的惰性气体压强)的交点;安全系数b为
斜截式
斜率的倒数。值得注意的时,系数a并不代表人类可以承受绝对环境压强为零的情况,这只是一个数学上的表达。
Bühlmann
模型中,
绝对环境压强
的最小值为0.5 atm/bar。

图一:Workman 与 Bühlmann 的M值图解,由 程程_Constance 译自 Eric C Baker
Workman M值方程的定义:
Bühlmann
M值
方程
的定义:
-
P
t.tol
.i.g. = 假想对照组织间隔内可承受的惰性气体压强
-
P
t
.i.g. =
假想对照组织间隔内的惰性气体压强
-
P
amb.
= 绝对环境压强
-
P
amb.tol
=
假想对照组织间隔可承受的绝对环境压强
-
a
= M值线性方程与Y轴交点
-
b =
M值线性方程
的斜率
-
数学表达:
Workman 与
Bühlmann M值间的互相转换
Workman 至 Bühlmann:
Bühlmann 至 Workman:
DCAP和DSAT的M值
许多技术潜水员也会注意到由 Hamilton 研究小组主导的减压计算与分析项目(Decompression Computation and Analysis Program,即DCAP)所使用的 16F6 M值。这组M值是由 Bill Hamilton 博士和他的同事在为瑞典海军研发新的空气减压计划表时确定的。除了空气潜水外,16F6 M值也可以很好地支持三混气。这一组M值也被各技术潜水员广泛地应用到自制的减压计划表格中。
许多潜水员都十分熟习由PADI派发的休闲潜水计划表。该计划表中使用的M值是由 Raymond E. Rogers 博士、Michael R. Powell 博士和其他来自PADI旗下的潜水科技有限公司(Diving Science and Technology Corp,DSAT)的同事开发与测试的。DAST的M值经过了大量的水下潜水员亲测和多普勒气泡检测,被认为是安全有效的。
各M值的比较
下表一至表四对本文中提到的各 “Haldanian” 减压算法使用的氮气和氦气的M值进行了比较。其中的M值均是以 Workman M值的形式表达的。从 Workman (1965年)到
Bühlmann
(1990年),M值的演化与精进是显而易见的。M值
在不断
地
被
调整得更加保守,
也在
不断
地
被更加严格的测试(例如使用多普勒仪探测潜水员体内微型气泡的存在)。

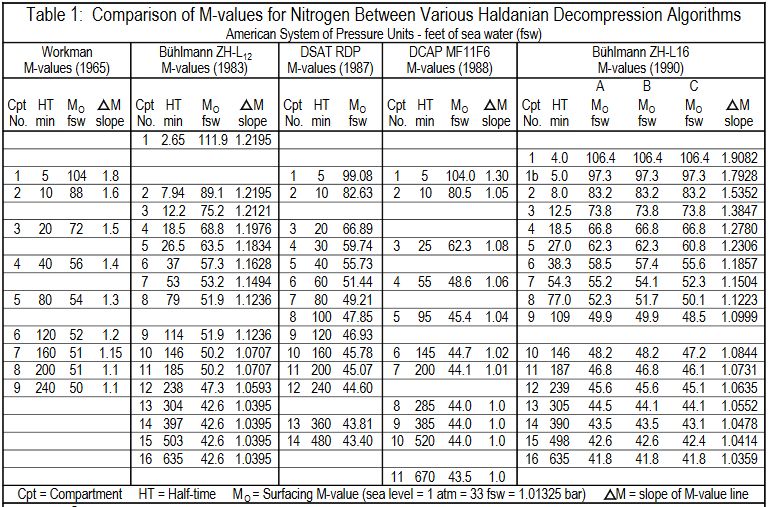
表一:各 “Haldanian” 减压算法中氮气M值的比较。从左至右依次为 Workman 的M值(1965年)、Bühlmann 的 ZH-L12 M值(1983年)、DSAT休闲潜水计划表的M值(1987年)、DCAP的 16F6 M值(1988年)和 Bühlmann 的 ZH-L16 M值(1990年)。表中的Cpt代表对照组织间隔,HT代表半饱和时间,M0为水面M值,△M为M值斜截式中的斜率。表中
压强
单位为美制,深度以英尺表示。
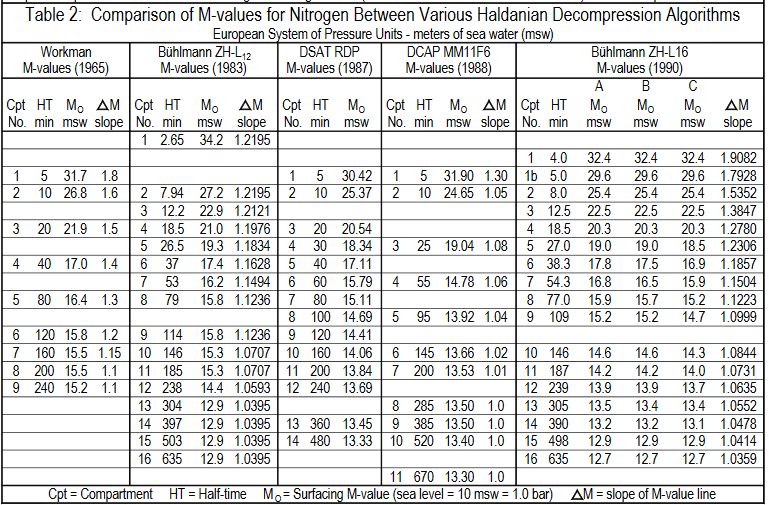
表二:各 “Haldanian” 减压算法中氮气M值的比较。从左至右依次为 Workman 的M值(1965年)、Bühlmann 的 ZH-L12 M值(1983年)、DSAT休闲潜水计划表的M值(1987年)、DCAP的 16F6 M值(1988年)和 Bühlmann 的 ZH-L16 M值(1990年)。表中的Cpt代表对照组织间隔,HT代表半饱和时间,
M0为水面M值,△M为M值斜截式中的斜率
。表中
压强
单位为欧制,深度以米表示。
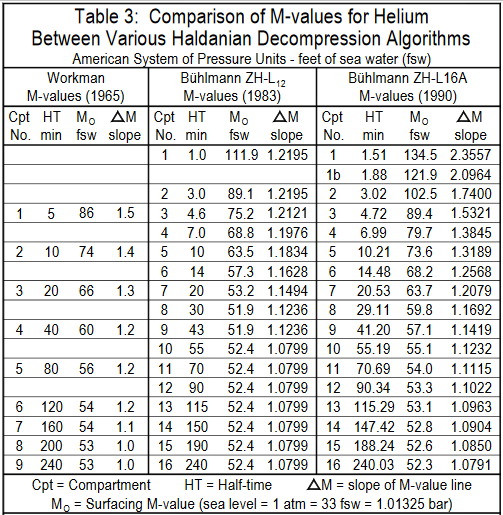
表三:各 “Haldanian” 减压算法中氦气M值的比较。从左至右依次为 Workman 的M值(1965年)、Bühlmann 的 ZH-L12 M值(1983年)和 Bühlmann 的 ZH-L16 M值(1990年)。表中的Cpt代表对照组织间隔,HT代表半饱和时间,
M0为水面M值,△M为M值斜截式中的斜率
。表中
压强
单位为美制,深度以英尺表示。

表四:各 “Haldanian” 减压算法中氦气M值的比较。从左至右依次为 Workman 的M值(1965年)、Bühlmann 的 ZH-L12 M值(1983年)和 Bühlmann 的 ZH-L16 M值(1990年)。表中的Cpt代表对照组织间隔,HT代表半饱和时间,M0为水面M值,△M为M值斜截式中的斜率。
表中压强单位为欧制,深度以米表示。
M值的一致性
通过比较各算法的M值,我们不难发现它们之间的差异并不是很大。换句话说,世界各地独立的减压研究者所得出的M值之间是存在一定的一致性的。这对广大潜水员来说是一个好的迹象,因为这表明了减压科学已经为人类人群中出现减压病症状确定了一个相对一致的临界值。
M值的表达方式
与 Workman 和 Bühlmann 的表现形式类似,M值通常都是以线性方程的形式来表达的。这种表达方式非常适合应用在计算机的软件编程中,因为线性方程可以随时计算出“动态”的M值。此外,该线性表达也使得M值可以在压力图上显示出来。
M值也可以用矩阵或表格的形式来表达。也就是说,我们可以将每组对照组织间隔在不同深度的M值预先算好并罗列在表格中,这种表达方式方便人们对各M值进行详细地比较和分析。一些早期的潜水电脑表和减压软件也是通过在M值表格中查找各减压站对应的M值来计算减压计划的。
M值的分类
M值通常可以归为两大类,一类适用于免减压潜水,一类适用于减压潜水。适用于免减压潜水的M值就是所有对照组织间隔的水面M值,即深度压强为0时M的值。DSAT 派发的休闲潜水计划表使用的M值就是
其中
一个例子。在设计免减压潜水计划表时,只需要确保各对照组织间隔内的惰性气体压强不超过水面M值即可,这样在潜水过程中,潜水员可以随时上升至水面且不出现
减压病的症状。当然,有一些免减压潜水的算法也考虑到了上升和下潜的速率。
适用于减压潜水的M值就是那些可用M值方程表达的M值。方程的斜率会随对照组织间隔的半饱和周期的改变而改变。通常来说,快组织细胞的斜率要大于慢组织细胞的斜率。这很好地反应了快组织细胞比慢组织细胞可以承受更大的超压这一理论。如果方程的斜率大于1,则表示该M值对应的对照组织间隔内可承受的惰性气体压强与其所处的环境压强差会随深度的增加而增大;如果方程的斜率等于1,则表示该
M值对应的对照组织间隔内可承受的惰性气体压强与其所处的环境压强差不会随深度的改变而改变;但无论在何种情况下,方程的斜率是永远不会小于1的,因为如果方程的斜率小于1的话,那么该方程的直线就会与周围环境压强准线相交,且在相交之后位于准线下方,这意味着此时对照组织间隔连环境压强都无法承受,这是不符合逻辑的。
环境压强准线
环境压强准线在M值图解中是非常重要的一条基准线。环境压强准线是一条穿过坐标轴原点,且斜率为1的直线。该直线上的点代表了对照组织间隔内惰性气体压强等于其所处环境压强的情况。当
对照组织间隔内惰性气体压强
超过其所处环境压强时(
即位于环境压强准线
上方的点),就会形成一个压强差。代表M值的直线则限制了该压强差的最大值。
减压区间
“减压区间”指的是M值图解中位于环境压强准线与M值直线之间的区域(如图三)。在溶解气体模型中,该区域代表组织细胞进入减压。从理论上说,对照组织间隔是需要一个正向的压强差(即内部压强大于外部压强)来触发“排气”或“减压”的。在某些情况下,即使
对照组织间隔
内惰性气体总分压小于所处环境压强,
对照组织间隔
也是可以排气的,例如在潜水员呼吸高氧分压的减压气体时。
在减压过程中,不同的对照组织间隔会依次进出其对应的
减压区间
,高效的减压计划都是基于进入减压区间的对照组织间隔内惰性气体负载的情况来设计的。通常来说,快组织细胞会较先进入减压区间并控制减压,当快组织细胞完成减压并退出减压区间后,较慢的组织细胞会依次进入减压区间接管接下来的减压进程。
混合气体的M值
当今的溶解气体模型引入了混合气体这一概念,这一概念指出尽管同一对照组织间隔内各惰性气体的半饱和周期不同,但其内部的惰性气体总压强应等于其内部各惰性气体分压的总和。
混合气减压算法必须可以处理呼吸气体中的多种惰性气体,例如三混气中的氮气和氦气。不同的减压算法对此情况下的M值的处理方式也有所不同。有些算法会对氮气和氦气都使用同一个M值,该M值
通常
是基于氮气的。
Bühlmann
的算法为氮气和氦气的M值计算了一个中间值,该值是根据对照组织间隔内氮气与氦气的分压比算出来的。在M值的线性方程中,氮气和氦气的混合安全系数a和b是通过如下方法计算而来的:
M值到底代表什么?
有些潜水员总误以为M值是“
罹患减压病
”和“不得
减压病
”之间一条黑白分明的准线,这或许可以解释为什么有些潜水员总是将自己的减压计划推到极限。然而一些潜水试验表明,这些极限,也就是M值,在某些情况下是不够充分的。而具体这些M值有多不充分,也因人而异,要视乎不同情况而定。因此,把M值看做是一条穿过模糊的灰色地带的直线(如图二)可能会更合适。这样模糊地定义M值是综合考虑了复杂的人体生理机制、人类个体间差异以及减压病的多种诱发因素的结果。
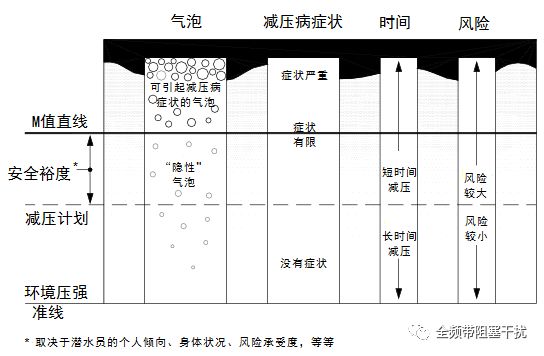
图二:把M值看做是一条穿过模糊的灰色地带的直线可能会更合适。该直线为绝大多数潜水员是否会高频次罹患减压病的临界值。
由 程程_Constance 译自 Eric C Baker
总的来说,溶解气体模型对广大潜水员来说还是行之有效的,与其相关的知识库也在不断地增长与丰富。例如,最初人们认为
组织细胞内
的惰性气体必须以溶解气体的形式存在,任何气泡的出现都会引发减压病。然而,现在我们知道在无减压病症状的潜水员体内也会存在一些“隐性”的微气泡。因此,在一次安全潜水中,惰性气体
实际上
是以两种形式存在于组织细胞内的:它们大部分处于溶解状态,极小一部分会成为“隐性”气泡。也就是说,M值不仅仅代表了组织细胞内可承受的惰性气体超压,也还代表了其可容忍的气泡总量。
















