
近来在深度学习中,卷积神经网络和循环神经网络等深度模型在各种复杂的任务中表现十分优秀。例如卷积神经网络(CNN)这种由生物启发而诞生的网络,它基于数学的卷积运算而能检测大量的图像特征,因此可用于解决多种图像视觉应用、目标分类和语音识别等问题。
但是,深层网络架构的学习要求大量数据,对计算能力的要求很高。神经元和参数之间的大量连接需要通过梯度下降及其变体以迭代的方式不断调整。此外,有些架构可能因为强大的表征力而产生测试数据过拟合等现象。这时我们可以使用正则化和优化技术来解决这两个问题。
梯度下降是一种优化技术,它通过最小化代价函数的误差而决定参数的最优值,进而提升网络的性能。尽管梯度下降是参数优化的自然选择,但它在处理高度非凸函数和搜索全局最小值时也存在很多局限性。
正则化技术令参数数量多于输入数据量的网络避免产生过拟合现象。正则化通过避免训练完美拟合数据样本的系数而有助于算法的泛化。为了防止过拟合,增加训练样本是一个好的解决方案。此外,还可使用数据增强、L1 正则化、L2 正则化、Dropout、DropConnect 和早停(Early stopping)法等。
增加输入数据、数据增强、早停、dropout 及其变体是深度神经网络中常用的调整方法。本论文作为之前文章《徒手实现 CNN:综述论文详解卷积网络的数学本质 》的补充,旨在介绍开发典型卷积神经网络框架时最常用的正则化和优化策略。
主体论文:Regularization and Optimization strategies in Deep Convolutional Neural Network
论文地址:https://arxiv.org/pdf/1712.04711.pdf
摘要:卷积神经网络(ConvNet)在一些复杂的机器学习任务中性能表现非常好。ConvNet 架构需要大量数据和参数,因此其学习过程需要消耗大量算力,向全局最小值的收敛过程较慢,容易掉入局部极小值的陷阱导致预测结果不好。在一些案例中,ConvNet 架构与数据产生过拟合,致使架构难以泛化至新样本。为了解决这些问题,近年来研究者开发了多种正则化和优化策略。此外,研究显示这些技术能够大幅提升网络性能,同时减少算力消耗。使用这些技术的前提是全面了解该技术提升网络表达能力的理论原理,本论文旨在介绍开发 ConvNet 架构最常用策略的理论概念和数学公式。
正则化技术
正则化技术是保证算法泛化能力的有效工具,因此算法正则化的研究成为机器学习中主要的研究主题 [9] [10]。此外,正则化还是训练参数数量大于训练数据集的深度学习模型的关键步骤。正则化可以避免算法过拟合,过拟合通常发生在算法学习的输入数据无法反应真实的分布且存在一些噪声的情况。过去数年,研究者提出和开发了多种适合机器学习算法的正则化方法,如数据增强、L2 正则化(权重衰减)、L1 正则化、Dropout、Drop Connect、随机池化和早停等。
除了泛化原因,奥卡姆剃刀原理和贝叶斯估计也都支持着正则化。根据奥卡姆剃刀原理,在所有可能选择的模型中,能很好解释已知数据,并且十分简单的模型才是较好的模型。而从贝叶斯估计的角度来看,正则化项对应于模型的先验概率。
4.1 数据增强
数据增强是提升算法性能、满足深度学习模型对大量数据的需求的重要工具。数据增强通过向训练数据添加转换或扰动来人工增加训练数据集。数据增强技术如水平或垂直翻转图像、裁剪、色彩变换、扩展和旋转通常应用在视觉表象和图像分类中。
4.2 L1 和 L2 正则化
L1 和 L2 正则化是最常用的正则化方法。L1 正则化向目标函数添加正则化项,以减少参数的值总和;而 L2 正则化中,添加正则化项的目的在于减少参数平方的总和。根据之前的研究,L1 正则化中的很多参数向量是稀疏向量,因为很多模型导致参数趋近于 0,因此它常用于特征选择设置中。机器学习中最常用的正则化方法是对权重施加 L2 范数约束。
标准正则化代价函数如下:
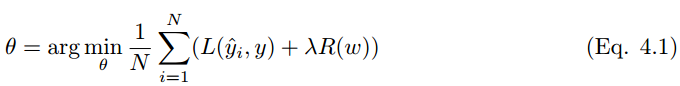
其中正则化项 R(w) 是:

另一种惩罚权重的值总和的方法是 L1 正则化:

L1 正则化在零点不可微,因此权重以趋近于零的常数因子增长。很多神经网络在权重衰减公式中使用一阶步骤来解决非凸 L1 正则化问题 [19]。L1 范数的近似变体是:

另一个正则化方法是混合 L1 和 L2 正则化,即弹性网络罚项 [20]。
在《深度学习》一书中,参数范数惩罚 L2 正则化能让深度学习算法「感知」到具有较高方差的输入 x,因此与输出目标的协方差较小(相对增加方差)的特征权重将会收缩。而 L1 正则化会因为在方向 i 上 J(w; X, y) 对 J(w; X, y) hat 的贡献被抵消而使 w_i 的值变为 0(J(w; X, y) hat 为 J(w; X, y) 加上 L1 正则项)。此外,参数的范数正则化也可以作为约束条件。对于 L2 范数来说,权重会被约束在一个 L2 范数的球体中,而对于 L1 范数,权重将被限制在 L1 所确定的范围内。
4.3 Dropout
Bagging 是通过结合多个模型降低泛化误差的技术,主要的做法是分别训练几个不同的模型,然后让所有模型表决测试样例的输出。而 Dropout 可以被认为是集成了大量深层神经网络的 Bagging 方法,因此它提供了一种廉价的 Bagging 集成近似方法,能够训练和评估值数据数量的神经网络。
Dropout 指暂时丢弃一部分神经元及其连接。随机丢弃神经元可以防止过拟合,同时指数级、高效地连接不同网络架构。神经元被丢弃的概率为 1 − p,减少神经元之间的共适应。隐藏层通常以 0.5 的概率丢弃神经元。使用完整网络(每个节点的输出权重为 p)对所有 2^n 个 dropout 神经元的样本平均值进行近似计算。Dropout 显著降低了过拟合,同时通过避免在训练数据上的训练节点提高了算法的学习速度。
4.4 Drop Connect
Drop Connect 是另一种减少算法过拟合的正则化策略,是 Dropout 的一般化。在 Drop Connect 的过程中需要将网络架构权重的一个随机选择子集设置为零,取代了在 Dropout 中对每个层随机选择激活函数的子集设置为零的做法。由于每个单元接收来自过去层单元的随机子集的输入,Drop Connect 和 Dropout 都可以获得有限的泛化性能 [22]。Drop Connect 和 Dropout 相似的地方在于它涉及在模型中引入稀疏性,不同之处在于它引入的是权重的稀疏性而不是层的输出向量的稀疏性。
4.5 早停法
早停法可以限制模型最小化代价函数所需的训练迭代次数。早停法通常用于防止训练中过度表达的模型泛化性能差。如果迭代次数太少,算法容易欠拟合(方差较小,偏差较大),而迭代次数太多,算法容易过拟合(方差较大,偏差较小)。早停法通过确定迭代次数解决这个问题,不需要对特定值进行手动设置。
优化技术
5.1 动量(Momentum)
随机梯度下降和小批量梯度下降是机器学习中最常见的优化技术,然而在大规模应用和复杂模型中,算法学习的效率是非常低的。而动量策略旨在加速学习过程,特别是在具有较高曲率的情况下。动量算法利用先前梯度的指数衰减滑动平均值在该方向上进行回退 [26]。该算法引入了变量 v 作为参数在参数空间中持续移动的速度向量,速度一般可以设置为负梯度的指数衰减滑动平均值。对于一个给定需要最小化的代价函数,动量可以表达为:
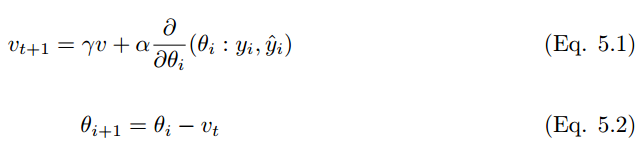
其中 α 为学习率,γ ∈ (0, 1] 为动量系数,v 是速度向量,θ是保持和速度向量方向相同的参数。一般来说,梯度下降算法下降的方向为局部最速的方向(数学上称为最速下降法),它的下降方向在每一个下降点一定与对应等高线的切线垂直,因此这也就导致了 GD 算法的锯齿现象。虽然 SGD 算法收敛较慢,但动量法是令梯度直接指向最优解的策略之一。在实践中,γ初始设置为 0.5,并在初始学习稳定后增加到 0.9。同样,α 一般也设置地非常小,因为梯度的量级通常是比较大的。
5.2 Nesterov 加速梯度(NAG)
Nesterov 加速梯度(NAG)和经典动量算法非常相似,它是一种一阶优化算法,但在梯度评估方面有所不同。在 NAG 中,梯度的评估是通过速度的实现而完成的。NAG 根据参数进行更新,和动量算法一样,不过 NAG 的收敛速度更好。在批量梯度下降中,与平滑的凸函数相比,NAG 的收敛速度超出 1/k 到 1/(k^2) [27]。但是,在 SGD 中,NAG 无法提高收敛速度。NAG 的更新如下:
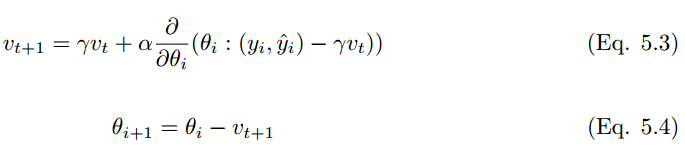
动量系数设置为 0.9。经典的动量算法先计算当前梯度,再转向更新累积梯度。相反,在 NAG 中,先转向更新累积梯度,再进行校正。其结果是防止算法速度过快,且增加了反应性(responsiveness)。
5.3 Adagrad
Adagrad 亦称为自适应梯度(adaptive gradient),允许学习率基于参数进行调整,而不需要在学习过程中人为调整学习率。Adagrad 根据不常用的参数进行较大幅度的学习率更新,根据常用的参数进行较小幅度的学习率更新。因此,Adagrad 成了稀疏数据如图像识别和 NLP 的天然选择。然而 Adagrad 的较大问题在于,在某些案例中,学习率变得太小,学习率单调下降使得网络停止学习过程。在经典的动量算法和 Nesterov 中,加速梯度参数更新是对所有参数进行的,并且学习过程中的学习率保持不变。在 Adagrad 中,每次迭代中每个参数使用的都是不同的学习率。
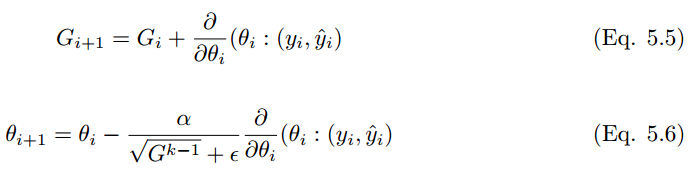
5.4 AdaDelta
AdaDelta 使用最近历史梯度值缩放学习率,并且和经典的动量算法相似,累积历史的更新以加速学习。AdaDelta 可以有效地克服 Adagrad 学习率收敛至零的缺点。AdaDelta 将累积过去平方梯度的范围限制在固定窗口 w 内,取代了经典动量算法累积所有历史梯度值的做法。在时间 t 运行的平均值计算 E[g^2](t) 依赖于过去的平均值和当前的梯度值。因此,该平均值计算可以表示为:
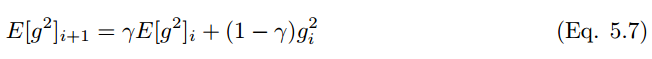
其中 γ 和动量项相同。实践中,该值通常设为 0.9 左右。根据等式 3.13,SGD 更新的等式为:
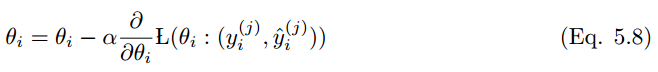
根据等式 5.6,Adagrad 的更新为:
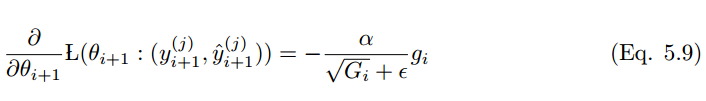
使用过往的平方梯度 替换对角矩阵 G_i,得到
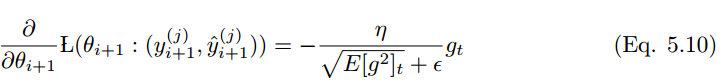
其中分母是梯度的平方根误差,
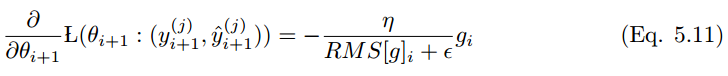
用 替换先前更新规则中的学习率 α,得到
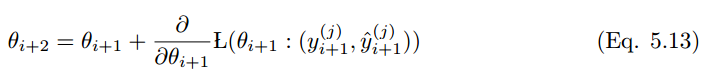
5.5 RMS prop
RMS prop 类似于 Adadelta 的较早的更新向量,
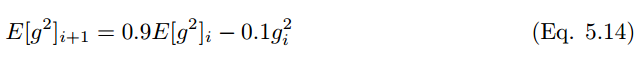
RMS prop 的更新规则如下:
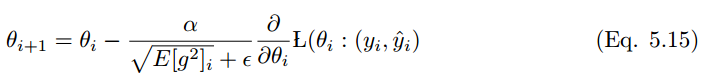
在 RMS prop 中,学习率除以平方梯度的指数衰减平均值。
5.6 Adam
1.Adam 优化算法的基本机制
Adam 算法和传统的随机梯度下降不同。随机梯度下降保持单一的学习率(即 alpha)更新所有的权重,学习率在训练过程中并不会改变。而 Adam 通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率。
Adam 算法的提出者描述其为两种随机梯度下降扩展式的优点集合,即:
适应性梯度算法(AdaGrad)为每一个参数保留一个学习率以提升在稀疏梯度(即自然语言和计算机视觉问题)上的性能。
均方根传播(RMSProp)基于权重梯度最近量级的均值为每一个参数适应性地保留学习率。这意味着算法在非稳态和在线问题上有很有优秀的性能。
Adam 算法同时获得了 AdaGrad 和 RMSProp 算法的优点。Adam 不仅如 RMSProp 算法那样基于一阶矩均值计算适应性参数学习率,它同时还充分利用了梯度的二阶矩均值(即有偏方差/uncentered variance)。具体来说,算法计算了梯度的指数移动均值(exponential moving average),超参数 beta1 和 beta2 控制了这些移动均值的衰减率。
移动均值的初始值和 beta1、beta2 值接近于 1(推荐值),因此矩估计的偏差接近于 0。该偏差通过首先计算带偏差的估计而后计算偏差修正后的估计而得到提升。
2.Adam算法

Adam论文地址:https://arxiv.org/abs/1412.6980
如上算法所述,在确定了参数α、β_1、β_2 和随机目标函数 f(θ) 之后,我们需要初始化参数向量、一阶矩向量、二阶矩向量和时间步。然后当参数 θ 没有收敛时,循环迭代地更新各个部分。即时间步 t 加 1、更新目标函数在该时间步上对参数θ所求的梯度、更新偏差的一阶矩估计和二阶原始矩估计,再计算偏差修正的一阶矩估计和偏差修正的二阶矩估计,然后再用以上计算出来的值更新模型的参数θ。

该算法更新梯度的指数移动均值(mt)和平方梯度(vt),而参数 β_1、β_2 ∈ [0, 1) 控制了这些移动均值(moving average)指数衰减率。移动均值本身使用梯度的一阶矩(均值)和二阶原始矩(有偏方差)进行估计。然而因为这些移动均值初始化为 0 向量,所以矩估计值会偏差向 0,特别是在初始时间步中和衰减率非常小(即β接近于 1)的情况下是这样的。但好消息是,初始化偏差很容易抵消,因此我们可以得到偏差修正(bias-corrected)的估计 m_t hat 和 v_t hat。
注意算法的效率可以通过改变计算顺序而得到提升,例如将伪代码最后三行循环语句替代为以下两个:
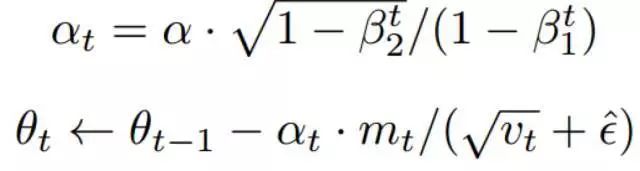
3. Adam 的更新规则


4. 初始化偏差修正
正如本论文第二部分算法所述,Adam 利用了初始化偏差修正项。本部分将由二阶矩估计推导出这一偏差修正项,一阶矩估计的推导完全是相似的。首先我们可以求得随机目标函数 f 的梯度,然后我们希望能使用平方梯度(squared gradient)的指数移动均值和衰减率 β_2 来估计它的二阶原始矩(有偏方差)。令 g1, …, gT 为时间步序列上的梯度,其中每个梯度都服从一个潜在的梯度分布 gt ~ p(gt)。现在我们初始化指数移动均值 v0=0(零向量),而指数移动均值在时间步 t 的更新可表示为: 其中 gt^2 表示 Hadamard 积 gt⊙gt,即对应元素之间的乘积。同样我们可以将其改写为在前面所有时间步上只包含梯度和衰减率的函数,即消去 v:

我们希望知道时间步 t 上指数移动均值的期望值 E[vt] 如何与真实的二阶矩 相关联,所以我们可以对这两个量之间的偏差进行修正。下面我们同时对表达式(1)的左边和右边去期望,即如下所示:
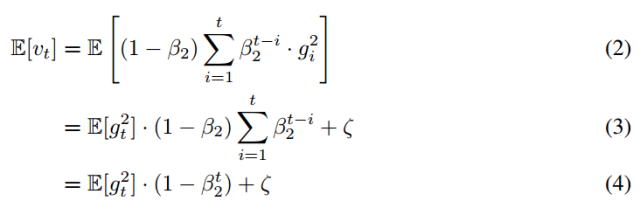
如果真实二阶矩 E[g^2] 是静态的(stationary),那么ζ = 0。否则 ζ 可以保留一个很小的值,这是因为我们应该选择指数衰减率 β1 以令指数移动均值分配很小的权重给梯度。所以初始化均值为零向量就造成了只留下了 (1 − βt^2 ) 项。我们因此在算法 1 中除以了ζ项以修正初始化偏差。
在稀疏矩阵中,为了获得一个可靠的二阶矩估计,我们需要选择一个很小的 β2 而在许多梯度上取均值。然而正好是这种小β2 值的情况导致了初始化偏差修正的缺乏,因此也就令初始化步长过大。
5.7 Nadam
Nadam 是 NAG 和 Adam 优化器的结合 [28]。如果过往历史平方梯度的指数衰减平均值为 v_t,而过往历史梯度的指数衰减平均值为 m_t,那么经典动量更新规则如下:
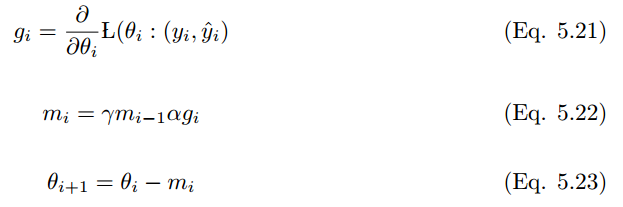
我们需要修改动量规则以获得 Nadam 优化器。因此将上述公式扩展为:

NAG 的修改如下:
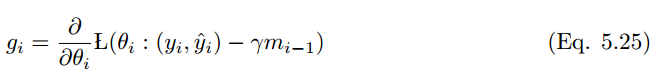

可以通过更新梯度 g_t 时(第一次)和更新参数 θ_t+1(第二次)修改 NAG,而不是两次更新动量。因此动量向量直接更新参数可以表述如下:

为了添加 NAG 到 Adam,需要使用当前的动态向量替换先前的动态向量。因此,通过 m hat 和 m_t 扩展上述公式,Adam 更新规则如下:
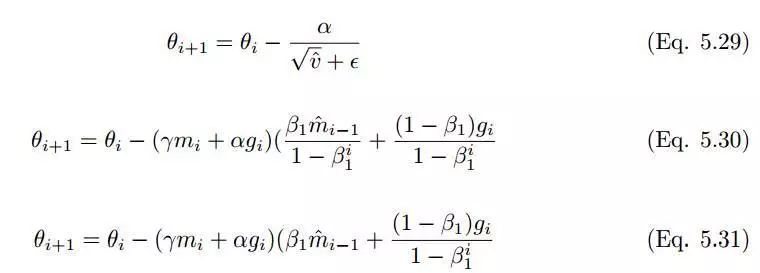
利用先前时间步动量向量的偏差修正估计更新 Nadam 优化器的规则,如下:
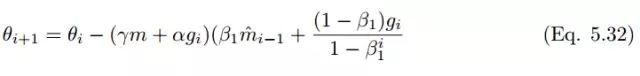

媒体合作请联系:
邮箱:[email protected]














