月供是怎么回事？

很多人买房子，买汽车，买大件商品，都会按揭，从银行或是金融机构按一定的利息在一定期限内贷款，然后按月还款，就是俗称的月供，每月还固定数量的钱，包括了利息和本金。

那么，这个背后到底是个什么逻辑，是怎么工作的呢？

首先，要了解“世界第八大奇观”，也是人类最伟大发明之一的复利。复利就是复合利息，它是指每年的收益还可以产生收益，具体是将整个借贷期限分割为若干段，前一段按本金计算出的利息要加入到本金中，形成增大了的本金，作为下一段计算利息的本金基数，直到每一段的利息都计算出来，加总之后，就得出整个借贷期内的利息，简单来说就是俗称的利滚利。复利的计算公式：

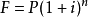
其中：P=本金（现值，Present Value)；i=利率；n=持有期限。

复利的力量是巨大的。印度有个古老故事，国王与象棋国手下棋输了，国手要求在第一个棋格中放上一粒麦子，第二格放上两粒，第三格放上四粒，即按复利增长的方式放满整个棋格。国王以为这个棋手可以得到一袋麦子，结果却是全印度的麦子都不足以支付。

接下来，要了解货币的时间价值，也就是贴现，钱越来越不值钱。明年的100元的购买力，由于通货膨胀，不如今天的100元。也就是说，任何将来的钱，都能按照利率折算回或是还原成今天的钱。它和计息是亲兄弟，计息是你将现在的货币借给别人一段时间到未来某个时刻收回，别人支付给你这段时间的货币增值额。而贴现就是计息的反过程，你将未来某个时刻的货币在现在就收回，就要扣除这段时间的货币增值额。

你以后每个月给银行的还款，就是将来的钱，而你现在拿到的贷款，就是现在的钱。那银行要保证你将来还的钱和你现在拿到的现金是等值的。

假设你以 i 的利息，借了一个 n 月的贷款 P，也就是说，你现在拿到了 P 值的现金。然后，你应该每月还钱 A 值。将来每个月的 A 值，都能贴现（折算）到今天的现金价值，这些所有贴现的和应该恰好等于你现在的贷款额 P。

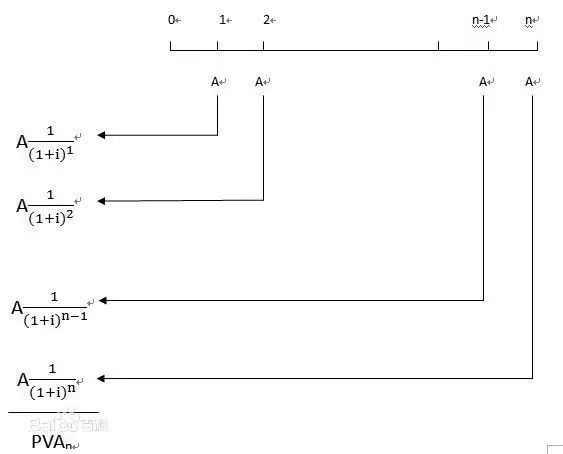
所有未来的还款，贴现到今天的现金值：

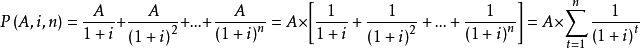
两边同时乘以 1+i，得到：

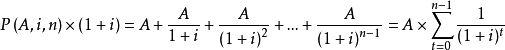
上面两式想减，得到：

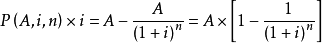
两边同时除以 i，得到：

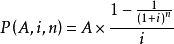
这个就是每个月月供后面的逻辑和数学基础。每个月还的钱都必须贴现为价钱时刻的现金值，现金值部分是用来还本的，而差额部分就是价钱的利息。

如果做价值投资，大家经常会听到DCF模型，也就是现金流量贴现。

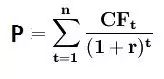
其中：P一企业的评估值（现值）； n一企业的寿命； CFt一企业在 t 时刻产生的现金流； r一反映预期现金流的折现率。

和这个是同出一辙，背后的逻辑是完全一致的。