一个机器人站在迷宫的起始位置,下图中的左下角。每一个位置,机器人有四个移动方向,左,右,上,下,当然,对于边缘情况,它的行动可能被限制。比如,在起始位置,它只能上移或是右移。如果某个移动让它碰到了障碍,那么它就被禁止往那个方向移动。在这些设置和条件的情况下,机器人如何能够通过自学习走出迷宫,也就是说,从迷宫的右上角出来?
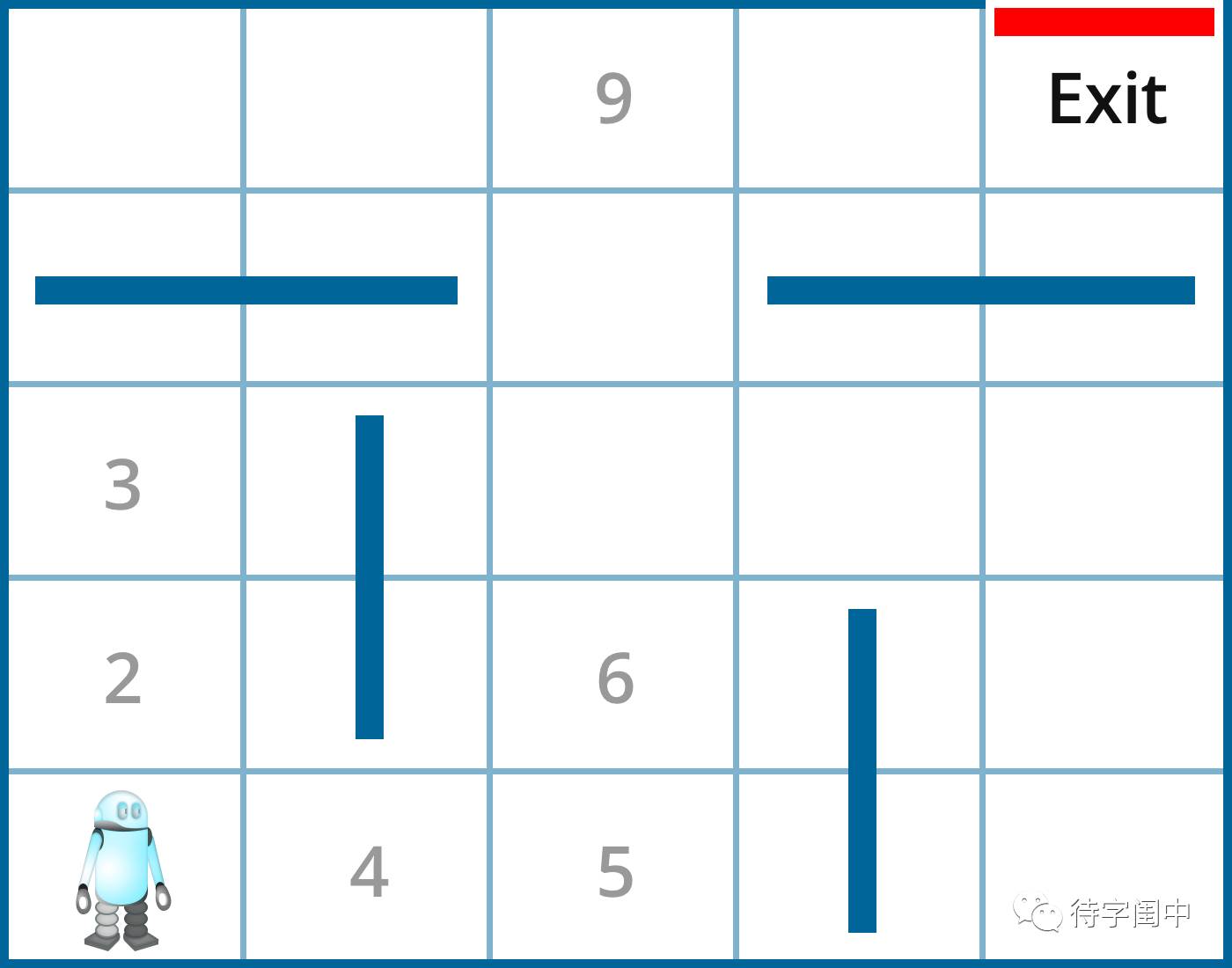
这是一个典型的强化学习(reinforcement learning)的例子。它直接将机器人的行动和产生的结果联系起来,而不需要机器人学习一个复杂的行动和结果的关系。机器人基于行动的奖赏和惩罚来学习如何走出迷宫。当机器人的移动造成了撞到障碍,那么它收到惩罚-1分。当它到达一个开阔地带,那么它收到奖赏0分(因为是它应该做的事情,不奖不罚)。当它到达出口,那么它收到一个大大的奖赏100分。这种反馈就是鼓励机器人做某个动作,或是防止做某个动作的“强化”。
强化学习是从交互中学习,从而成功达到一个目标。学习者和决策者称作是智能体(比如例中的机器人)。智能体交互的所有外部一切称作是环境(比如例中的迷宫)。这些交互持续进行,智能体选择某些行动,环境响应这些行动并且呈现一些新的情境给智能体。同时,环境给出一些奖赏,表现为特殊的数值,而这些数值是智能体希望长期最大化的。一个对环境,包括奖赏如何确定,的完整说明,定义了一个任务,即一个强化学习问题的实例。
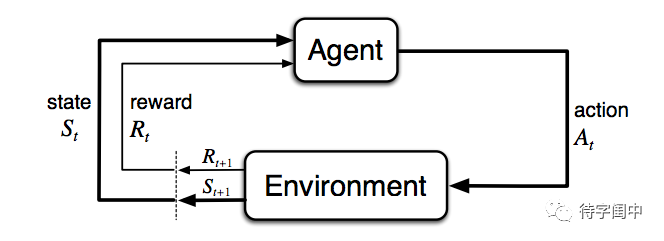
更确切的说,智能体和环境在离散的时间序列上交互,t = 0, 1, 2, 3, ... 在每个时间步t,智能体收到环境状态的某种表示 St ∈ S,其中 S 是所有可能环境状态的集合。然后智能体选择一个行动 At ∈ A(St),其中 A(St) 是在状态 St 的所有可以选择的行动的集合。一个时间步之后,作为行动的部分结果,智能体收到一个数值奖赏 Rt+1 ∈ R ⊂ R,并且进入到一个新的环境状态 St+1。 智能体的目标就是最大化长期的累积奖赏(回报)。对于有限的时间序列,定义回报为时间步t之后的所有奖赏的和,目标就是使之最大。
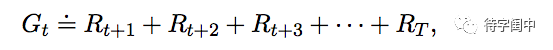
而对于无限的时间序列,当 T = ∞,上述的回报会区域无穷大,所以需要引入discounting。如下所示的 discounted 回报,γ ( 0 ≤ γ ≤ 1)叫做 discount rate。
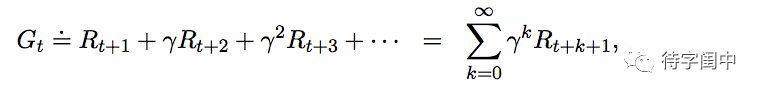
在强化学习的框架中,智能体根据环境状态的信号来做决定。那么,什么信息能构成环境状态的信号呢,这个就涉及到一个属性,叫做 Markov Property。通常情况下,环境状态的转换是和前面路径上的所有状态和行动相关的。如下所示。
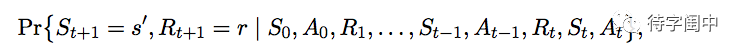
但是,如果说状态信号的转换具有 Markov Property,那么,它的下一个状态只与当前状态和行动相关。这样就大大简化了模型。
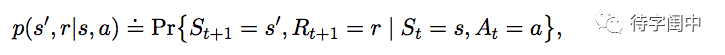
一个强化学习的任务如果满足 Makov Property,那么它就叫做 Markov Decision Process(MDP)。
知道了这个属性,就可以计算有关环境状态的各种信息了,比如,state-action 的期望奖赏。
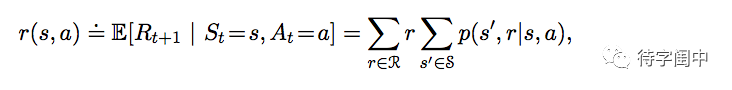
state-transition 概率。
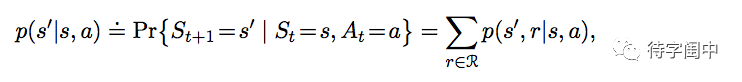
state-action-next-state 的期望奖赏。
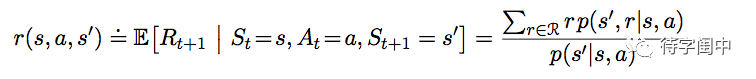
几乎所有强化学习的算法都涉及到估算 value functions(环境状态 states,或是 state-action 的 functions),而这些 functions 能估算智能体选择一个行动之后,它所处的下一个状态是不是比较好(how good)。而这个比较好(how good)定义为将来期望的奖赏(rewards),精确的说,就是期望回报。当然,智能体期望收到的奖赏和它采取的行动密切相关。也就是说,value functions 离不开特定的策略(policies,或
π
)。
一个策略, π, 是一个映射:从环境状态 s ∈ S 和 行动 a ∈ A(s) 到在环境状态 s 时采取行动 a 的概率
π(a|s)。有了这个知识,就可以定义一个环境状态 s 在策略
π 的 value,叫做 state-value function。
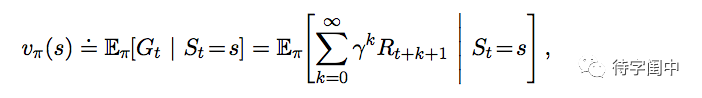
同理,定义一个环境状态 s 在策略
π 下采取行动
a 的 value,in state s under a policy π,叫做 action-value function。
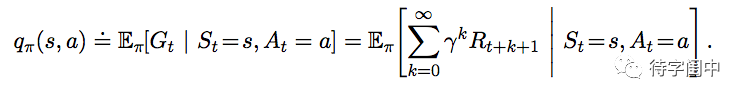
上述的 state-value function 和 value-action function 能够通过和环境的交互的体验估算出来。比如,一个智能体遵照策略
π,且对每一个状态维持一个从这个状态收到的回报的平均值,当这个状态被访问了接近无限次之后,那么这个平均值就会收敛到 state-value vπ(s)。如果对一个状态采取的每个行动记录一个平均值的话,那么这个平均值就会收敛到 action-value qπ (s, a)。
value function 的一个基本属性是满足特定的递归关系。这个就是著名的Bellman Equation。
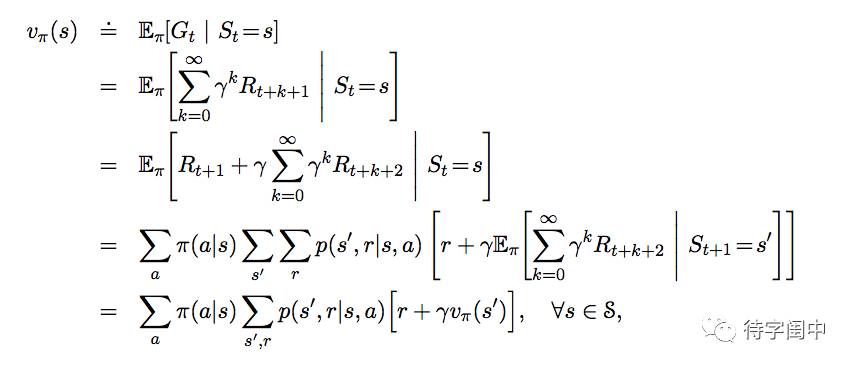
从下面的图示就很容易理解了。
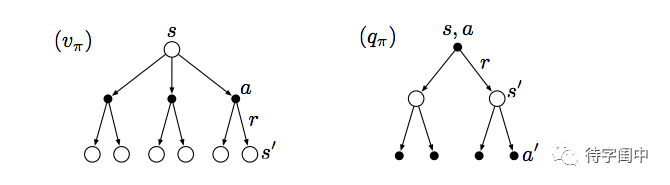
解决一个强化学习问题,粗略的说,是找到一个策略能够从长远获得许多的回报。对于有限的MDPs,精确的定义最有的策略如下:Value functions 定义了策略的偏序关系。一个策略 π 比另一个策略 π′ 好,如果且只有对于任何的环境状态,它的期望回报大于 π′。也就是说,对于所有的
s ∈ S,
π ≥ π′ iff vπ(s) ≥ vπ′(s)。总是有一个策略好于或是等于其它所有的策略,那么它就是最有的策略,表示成 π∗。
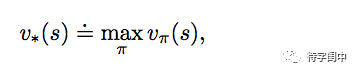
同理对于 action-value,它的最优q∗。
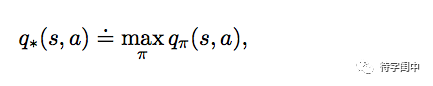
对于 state–action (s, a),在环境状态 s
采取行动 a 的期望回报一定是遵循最优的策略,所以,可以将 q∗ 按 v∗ 表达如下:
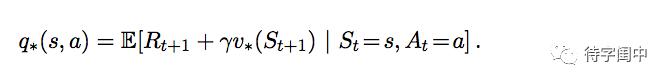
下面是Bellman optimality equation,它表达的是,在最优策略下,state value 必须等于在那个环境状态下采取的最好行动时的期望回报。
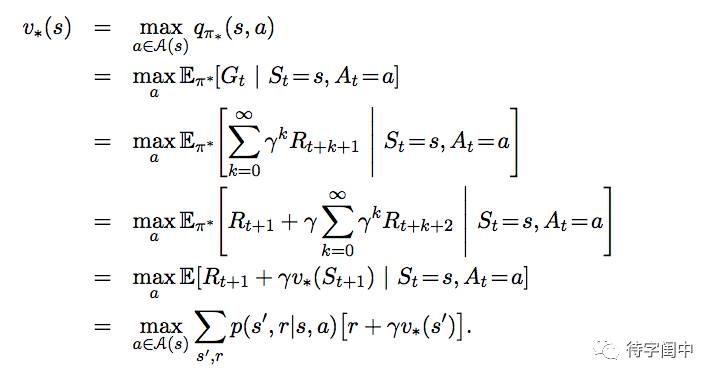
对于
q∗,
Bellman optimality equation 如下:

从下面的图示就很容易理解了。
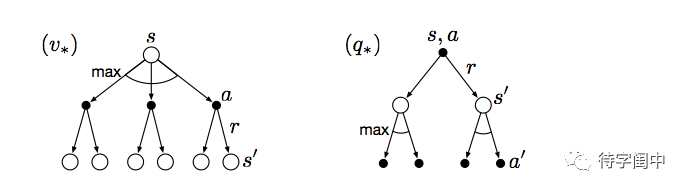
有了这些关于强化学习的问题的定义和基础知识之后,有不同的算法来迭代的解决。
下面介绍一种经常用到的强化学习方法 Q-learning。它学习 action-value function,Q,来近似 q*,最优的 action-value function。
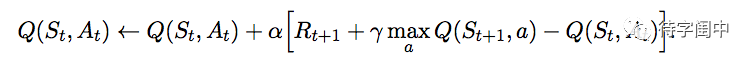
伪码的实现如下:

应用 Q-learning 到机器人走迷宫的问题。
Q(4, left) = 0 + 0.2 * (0 + 0.9 * Q(1,right) - 0)
Q(4, right) = 0+ 0.2 * (0 + 0.9 *
Q(5,up) -0)
这里,learning rate 是 0.2,且 discount rate 是 0.9。 在状态1的最好行动是 right,而状态5的是up。Q(1,right) 和 Q(5,up) 有不同的值,因为从状态1达到出口比从状态5需要更多的步数,也就是说,Q(5,up) 比
Q(1,right) 的 value 值更大。也正式这个原因,
Q(4,right) 的值比 Q(4, left) 大。那么,在状态4的最好的行动是right。重复迭代计算,最后机器人能通过 Q-learning 的方法自学习找到出口,走出迷宫。
参考文献:
-
Reinforcement learning explained https://www.oreilly.com/ideas/reinforcement-learning-explained?from=groupmessage&isappinstalled=0
-
Richard S. Sutton and Andrew G. Barto的《Reinforcement Learning:
An Introduction》





