
数据挖掘入门与实战 公众号: datadw
目录:
1. Boosting方法的简介
Boosting方法的基本思想:对于一个复杂的任务来说,将多个专家的判断进行适当的综合所得出的判断,要比其中任何一个专家单独的判断好. 实际上就是“三个臭皮匠顶个诸葛亮的道理。”(
对于分类问题而言, 给定一个训练集,求比较粗糙的分类规则(弱分类器)要比求精确的分类规则(强分类器)容易得多。Boosting方法就是从弱学习算法出发,反复学习,得到一系列弱分类器(又称基本分类器),然后组合这些弱分类器,构成一个强分类器。
对于Boosting方法来说,需要回答两个问题:
每一轮如何改变训练数据的权值或者概率分布
如何将若分类器组合成一个强分类器
2. AdaBoost算法
boosting 方法拥有多个版本,其中最流行的一个版本就是AdaBoost,即adaptive boosting.
对与上面提到的两个问题,AdaBoost的做法分别是:
具体算法流程描述如下:
假定给定一个二分类的训练数据集
T={(x1,y1),(x2,y2),⋯,(xN,yN)}" role="presentation">T={(x1,y1),(x2,y2),⋯,(xN,yN)}
其中,每个样本点由实例与标记组成. 实例 xi∈X⊆Rn" role="presentation">xi∈X⊆Rn
,标记 yi∈Y" role="presentation">yi∈Y⊆Rn" role="presentation">⊆Rn, X" role="presentation">X 是实例空间,Y" role="presentation">Y
是标记集合.
输入:训练数据集 T={(x1,y1),(x2,y2),⋯,(xN,yN)}" role="presentation">T={(x1,y1),(x2,y2),⋯,(xN,yN)}
,其中 xi∈X⊆Rn" role="presentation">xi∈X⊆Rn, yi∈Y={−1,+1}" role="presentation">yi∈Y={−1,+1}
;弱分类器;
输出:最终分类器 G(x)" role="presentation">G(x)
.
(1) 初始化训练数据的权值分布
D1={w11,⋯,w1i,⋯,w1N},w1N=1N,i=1,2,⋯,N" role="presentation">D1={w11,⋯,w1i,⋯,w1N},w1N=1N,i=1,2,⋯,N
初始化的时候让每个训练样本在基本分类器的学习中作用相同
(2) 对 m=1,2,⋯,M" role="presentation">m=1,2,⋯,M
(a) 使用具有权值分布 Dm" role="presentation">Dm
的训练数据学习,得到基本分类器
Gm(x):X⟶{−1,+1}" role="presentation">Gm(x):X⟶{−1,+1}
(b) 计算 Gm(x)" role="presentation">Gm(x)
在训练数据集上的分类误差
em=P(Gm(xi)≠yi)=∑i=1NwmiI(Gm(xi)≠yi)" role="presentation">em=P(Gm(xi)≠yi)=∑Ni=1wmiI(Gm(xi)≠yi)
(1)
(c) 计算 Gm(x)" role="presentation">Gm(x)
的系数
αm=12log1−emem" role="presentation">αm=12log1−emem
(2)
这里对数是自然对数. αm" role="presentation">αm
表示 Gm(x)" role="presentation">Gm(x) 在最终分类器中的重要性,由该式可知,当 em≤12" role="presentation">em≤12 时,αm≥0" role="presentation">αm≥0,并且 αm" role="presentation">αm 随着 em" role="presentation">em
的减小而增大,所以误差率越小的基本分类器在最终分类器中的作用越大.
(d) 更新训练数据集的权值分布
Dm+1={wm+1,1,⋯,wm+1,i,⋯,wm+1,N}" role="presentation">Dm+1={wm+1,1,⋯,wm+1,i,⋯,wm+1,N}
(3)
wm+1,i=wmiZmexp(−αmyiGm(xi)),i=1,2,⋯,N" role="presentation">wm+1,i=wmiZmexp(−αmyiGm(xi)),i=1,2,⋯,N
(4)
这里 Zm" role="presentation">Zm
是归一化因子.
Zm=∑i=1Nwmiexp(−αmyiGm(xi))" role="presentation">Zm=∑Ni=1wmiexp(−αmyiGm(xi))
它使 Dm+1" role="presentation">Dm+1
成为一个概率分布. 式 (4) 还可以写成:
wm+1,i={wmiZme−αm,Gm(xi)=yiwmiZmeαm,Gm(xi)≠yi" role="presentation">wm+1,i={wmiZme−αm,Gm(xi)=yiwmiZmeαm,Gm(xi)≠yi
由此可知,被基本分类器 Gm(x)" role="presentation">Gm(x)
误分类样本的权值得以扩大,而被正确分类样本的权值却得以缩小,因此误分类样本在下一轮学习中起更大作用.
(3) 构建基本分类器的线性组合
f(x)=∑i=1NαmGm(x)" role="presentation">f(x)=∑Ni=1αmGm(x)
得到最终分类器
G(x)=" role="presentation">G(x)=
sign(f(x))=" role="presentation">(f(x))=sign(∑m=1MαmGm(x))" role="presentation">(∑Mm=1αmGm(x))
线性组合 f(x)" role="presentation">f(x)
实现 M" role="presentation">M 个基本分类器的加权表决. f(x)" role="presentation">f(x) 的符号决定了实例 x" role="presentation">x 的类别,f(x)" role="presentation">f(x)
的绝对值表示分类的确信度.
3.基于单层决策树构建弱分类器
所谓单层决策树(decision stump, 也称决策树桩)就是基于简单的单个特征来做决策,由于这棵树只有一次分裂过程,因此实际上就是一个树桩。
首先通过一个简单的数据集来确保在算法实现上一切就绪.

def loadSimpData():
dataMat = np.matrix( [ [ 1., 2.1],
[ 2., 1.1],
[ 1.3, 1.],
[ 1., 1. ],
[ 2., 1. ] ] )
classLabels = [ 1.0, 1.0, -1.0, -1.0, 1.0 ]
return dataMat, classLabels

下图给出了上面数据集的示意图
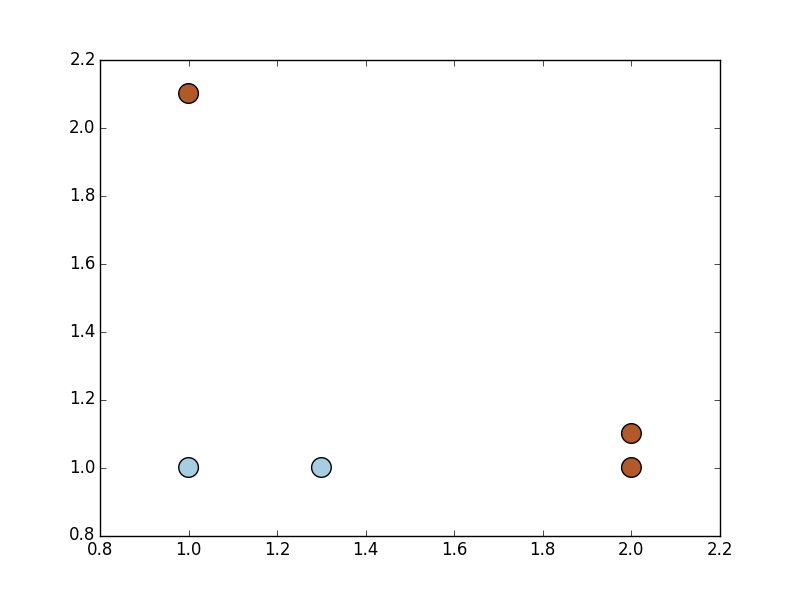
如果使用上面所述的单层决策树来对上面的样本点进行分类,即试着从某个坐标轴选择一个值(选择一条与坐标轴平行的直线)来将所有蓝色样本和褐色样本分开,这显然不可能。但是使用多棵单层决策树,就可以构建出一个能对该数据集完全正确的分类器.
首先给出单层决策树生成函数

上面两个函数作用是对于给定的数据集选出最佳的单层决策树.
4.完整的AdaBoost的算法实现
下面给出完整的AdaBoost的算法实现

运行结果
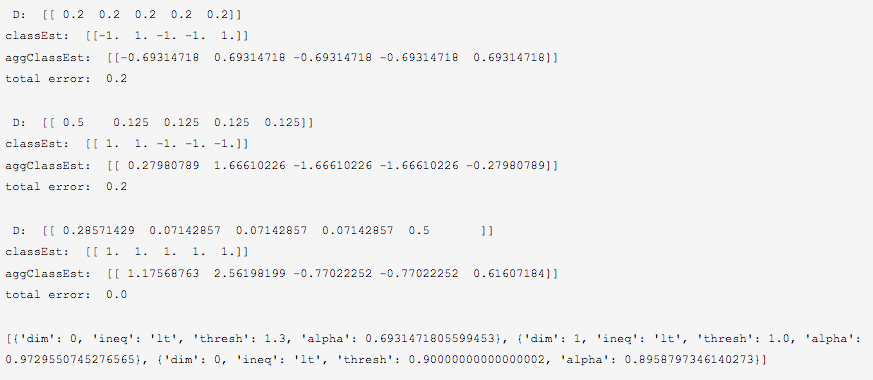
可以看到错误率逐步被降到0.0
, 最终的分类器包含3个基本分类器.
基于AdaBoost进行分类,需要做的就只是将弱分类器的训练过程从程序中抽取出来,然后应用到某个具体实例上去。每个弱分类器的结果以其对应的 alpha 值作为权值. 所有这些弱分类器的结果加权求和就得到了最后的结果.
测试

测试结果
[[-0.69314718]]
[[-1.66610226]]
[[-2.56198199]]
[[-1.]]
可以发现,随着迭代进行,数据点[0,0]
的分类确信度越来越强.
5.总结
AdaBoost的优点:泛化错误率低,可以用在大部分分类器上,无参数调整(自适应).
缺点:对离群点敏感.
via:http://blog.csdn.net/zdy0_2004/article/details/49894655
新浪微博名称:大数据_机器学习
数据挖掘入门与实战
搜索添加微信公众号:datadw
教你机器学习,教你数据挖掘

长按图片,识别二维码,点关注
公众号: weic2c
据分析入门与实战

长按图片,识别二维码,点关注















