图论曾经是本宫小学时非常敬畏的内容。为什么是小学？因为那时候有一本奥数辅导书叫作《华罗庚数学》，在六年级的那一册中即有图论相关的内容。

不好意思，一不小心就暴露年龄了。。。

咳咳，进入今天的正题，如何利用CytoScape的插件分析网络图的拓扑结构筛选关键基因。

1.0材料准备和插件安装

今天举的网络图的例子是从STRING上导出的PPI蛋白质网络图。

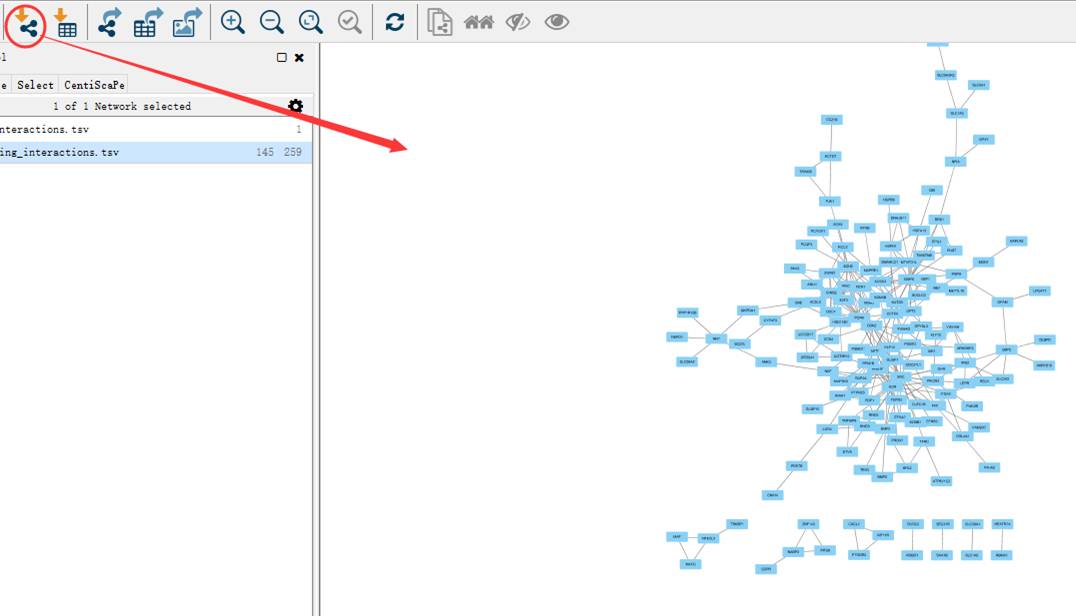
用的插件是Cytoscape中的 CentiScape 和 MCODE 。我们可以在 App Manager 中下载到这两个插件。

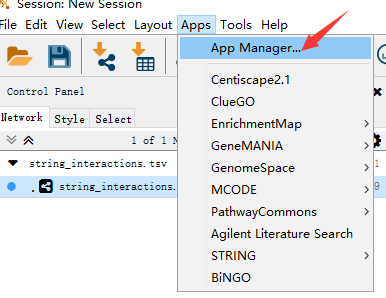
1.2 根据节点的中心度筛选基因

首先我们分析节点的 中心度（Centrality） ，最常见的度量节点Centrality的方式有三种： 点度中心性（Degree Centrality，DC）、接近中心性（Closeness Centrality，CC）和中介中心性（Betweenness Centrality，BC） 。

利用CentiScape我们可以算出degree，betweenness和closeness的值。

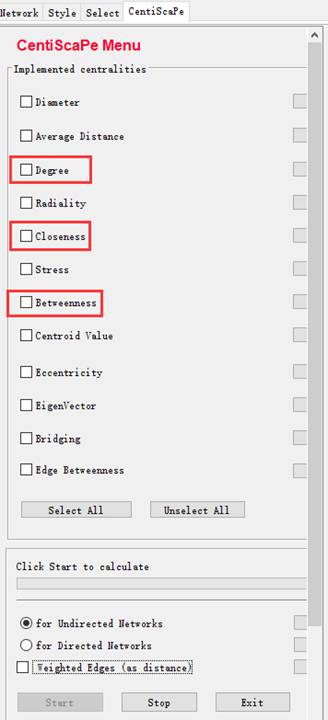
我们可以根据算出的中心度来对网络中的基因进行筛选

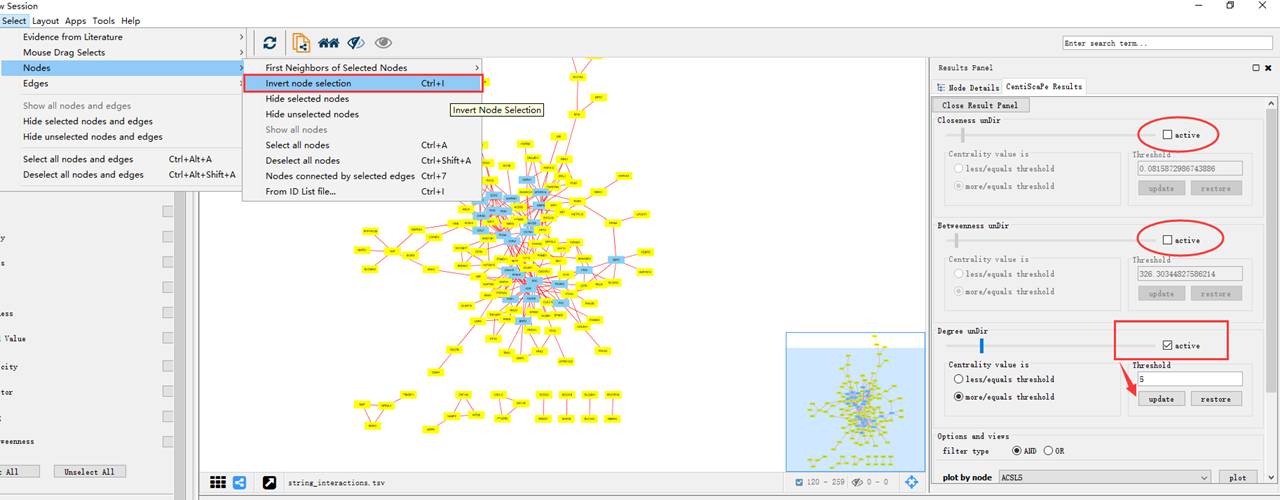
文章举例：

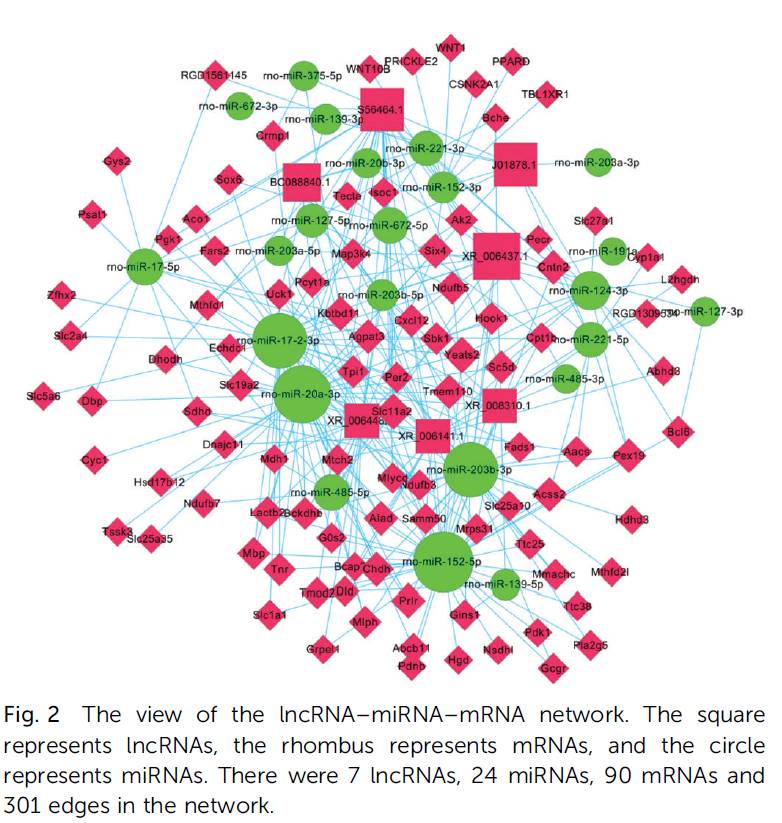
Reconstruction and analysis of the lncRNA–miRNA–mRNA network based on
competitive endogenous RNA reveal functional lncRNAs in rheumatoid arthritis （Molecular BioSystems，IF=2.85）

通过计算节点在网络中的Degree来评价基因的重要性。

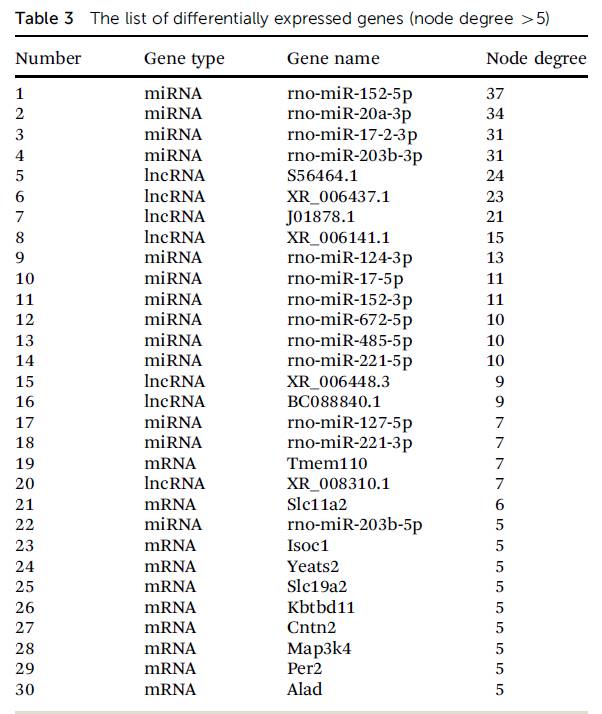
k 核解析（ k -core decomposition）

k 核解析可以帮助我们筛选出网络中的稳定结构，缩小研究的范围。虽然很多时候这样的稳定结构我们一眼就能看出来，因为那一团基因中两两之间都有联系！但是口说无凭，我们还是需要作一番分析才行！

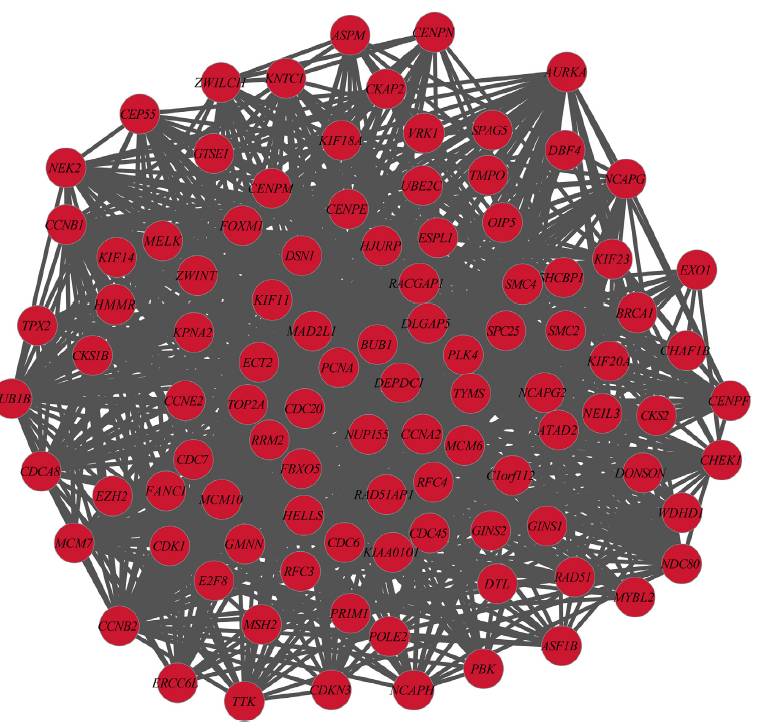
Identification of genes associated with melanoma metastasis

CytoScape中我们选择MOCE插件即可完成 k -核解析，K-core的地方可以设置k-core的阈值。

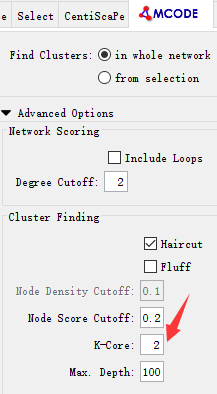
我们可以得到各种各样的子网络（subnetwork），并可以在CytoScape中创建新的网络。

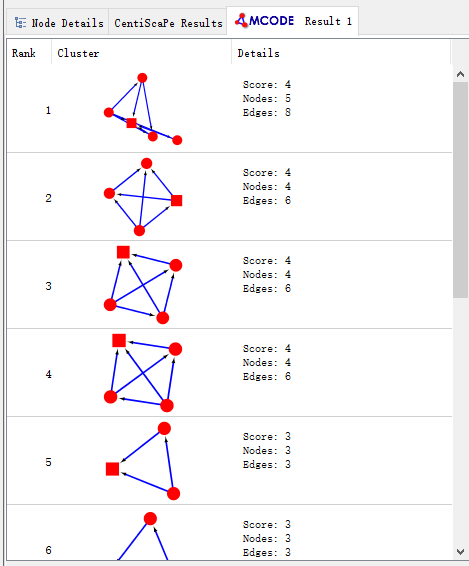
文章举例：

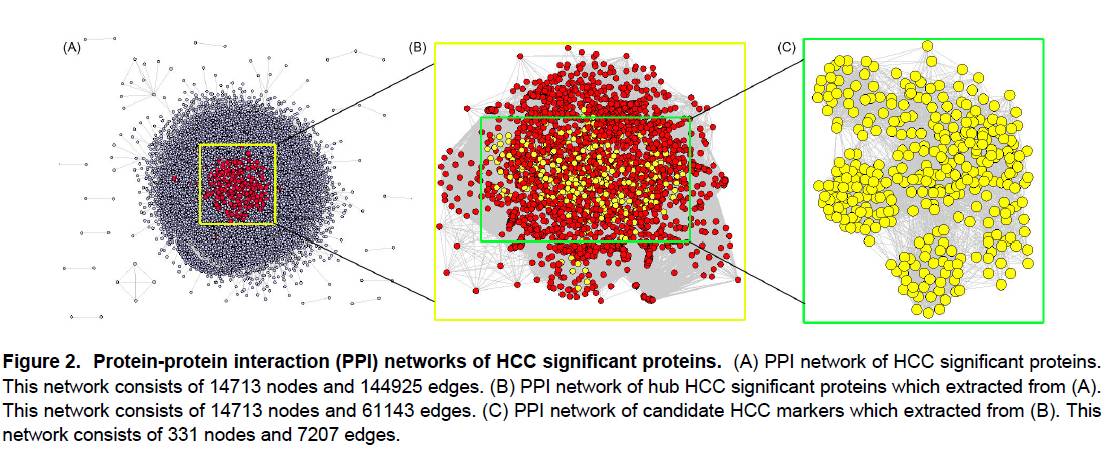
Identification of GRB2 and GAB1 Coexpression as an Unfavorable Prognostic Factor for Hepatocellular Carcinoma by a Combination of Expression Profile and Network Analysis（PLOS ONE，IF=3.11）

利用k-value在内的网络拓扑结构参数筛选网络中的关键基因。

2.1 中心度

我们先介绍一下 中心度（Centrality）中的 三个概念，以下我们讨论的都是无向（Undirected）网络。

点度中心性（Degree Centrality，DC）

举个简单的例子，我微信上有20个好友，你有50个，那么我的degree就是20，你是50；假设我和你两人的好友都不认识，我和你两个人的朋友圈构成了一个简单的网络，2个节点（我和你）和70个Edge（70个朋友关系），在这个网络中，你的degree是50，你的DC值就是50/70，而我的degree是20，WC值则是20/70。这一数据结果意味着你的点度中心度比我高，社交圈子比我广。

中介中心性（Betweenness Centrality，BC）

中介中心性指的是一个节点担任其它两个节点之间最短路的桥梁的次数。 计算网络中任意两个节点的所有最短路径，如果这些最短路径中有很多条都经过了某个节点，那么就认为这个节点的中介中心性高。 一个节点充当“中介”的次数越高，它的中介中心度就越大。

下面这个简单的网络结构中，A-C必须要经过B，B就充当了一次中介，整个网络中两点之间共有6条路径，其中A-D，A-C，D-A，C-A需要经过B，所以B的 Betweenness 为4，BC值为4/6。

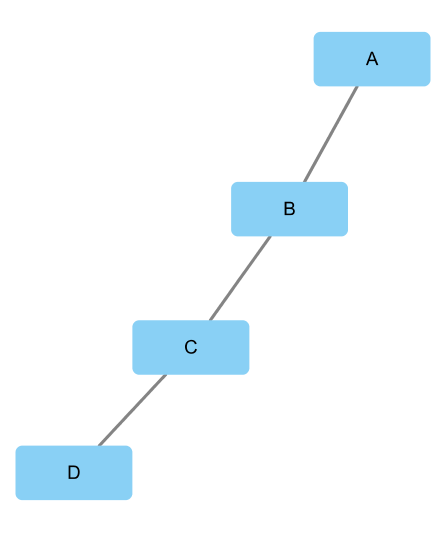
BC值高的点就像身边不停给你介绍相亲对象的李大婶，她认识的人就是莫名的多，感觉整个小区的人她都认识，然后你通过她结识了各色相亲对象。

接近中心性（Closeness Centrality，CC）

接近中心性需要考量每个结点到其它结点的最短路的平均长度，也就是说，对于一个结点而言，它距离其它结点越近，那么它的中心度越高。

还是以这个图为例，B到其它所有节点的距离之和为4，所以它的CC值为1/4，而A则是1/6。

比如常说大武汉是九省通衢，指的就是它到各地的距离都很短，总和较小。

参考文献： Analysis D D and Raya V 2013 Social Network Analysis, Methods and Measurements Calculations pp 2–5

2.2 k 核解析（ k -core decomposition）

所谓 k - 核 ( k - core ) 是指以 “ 剥洋葱 ” 式的操作 , 从网络中提取满足以下条件的子网络 ： 该子网络中的每个节点至少与