1 柏拉图多面体
正多面体，是指多面体的各个面都是全等的正多边形，并且各个多面角都是全等的多面角。正多面体一共只有5个，最早由古希腊哲学家柏拉图发现，所以也称柏拉图多面体。
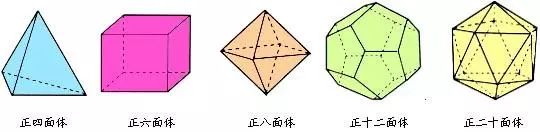
柏拉图认为世界由四古典元素组成，其形状如正多面体中的其中四个。
-
火
的热让人感到尖锐和刺痛，好像小小的
正四面体
。
-
空气
是用
正八面体
制成的，可以粗略感受到，它极细小的结合体十分顺滑。
-
当
水
放到人的手上，它会自然流出，那它就应该是由很多小球所组成，好像
正二十面体
。
-
土
与其他的元素相异，因为它可以被堆栈，正如
正六面体（正立方体）
。
剩下没有用的正多面体——
正十二面体
，柏拉图以不清晰的语调写：“神使用正十二面体以整理整个天空旳星座。”柏拉图的学生亚里士多德添加了第五个元素——以太，并认为天空是用此组成，但他没有将以太和正十二面体联系。
2 欧拉公式
我们知道，空间中的多面体由顶点（
）、面（
）、棱（
）组成，将它们的数量简记为
、
、
，现在来研究一下三者之间的关系，列个表：
|
类型
|
顶点数
|
面数
|
棱数
|
计算
|
|
正四面体
|
4
|
4
|
6
|
2
|
|
正六面体
|
8
|
6
|
12
|
2
|
|
正八面体
|
6
|
8
|
12
|
2
|
|
正十二面体
|
20
|
12
|
30
|
2
|
|
正二十面体
|
12
|
20
|
30
|
2
|
我们发现，
的值总是2，这是巧合吗？还是说这是正多面体满足的特有规律？
来看一个不规则多面体：
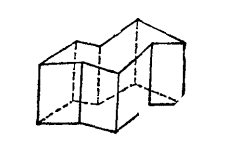同样地，我们列表：
|
类型
|
顶点数
|
面数
|
棱数
|
计算
|
|
不规则多面体
|
16
|
10
|
24
|
2
|
仍有
，这似乎表明任意多面体的顶点数、面数、棱数都满足这个数量关系。
事实上，数学家欧拉证明了对于任意
简单多面体
，都有
这个恒等式成立，它被称之为
多面体欧拉公式
。
这里需要说明一下，所谓
简单多面体
指的是
同胚
于球面的多面体（
同胚
是一个拓扑学概念，你可以简单理解为如果在一个多面体内部吹气，它能膨胀变为一个球，那么可以认为它与球同胚）。
欧拉公式的完整形式是
这里的
称为
欧拉示性数
，它是一个拓扑不变量，与空间体
的性质有关，当
为简单多面体时，有
3 证明
现在我们来研究一下为什么
对于简单多面体都成立。
我们以正六面体（即正方体）为例，假设在正六面体中，有
在这里
是一个未知数，我们的目标是证明
是常数
.
可以通过一些简单的变换证明多面体欧拉公式，具体操作如下：
3.1 去面
我们将正六面体进行“压缩”，使其变成上底面为小正方形的几何体。
注意到在这个过程中，并没有改变原来的顶点数、棱数、面数，因此仍有
这时再将其“拍扁”，使其成为一个二维图形。
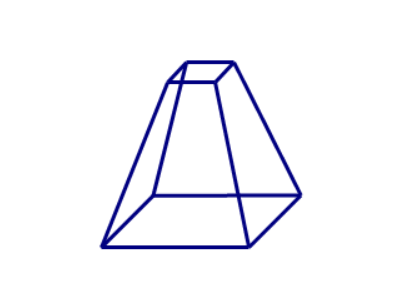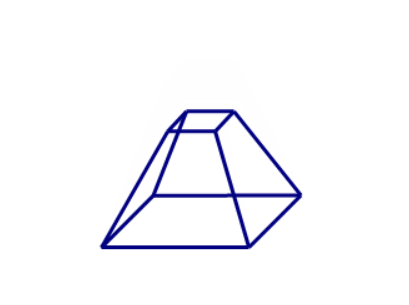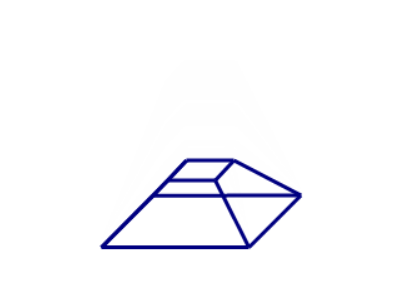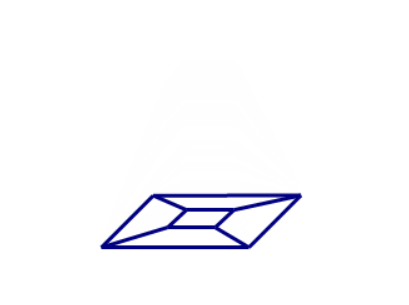
在这个由三维向二维转化的过程中，最终的图形相比原来的几何体其面数是少了
的（因为上下底面合并为了同一个面），记二维图形的面数为
,则有
3.2 加棱
在完成了“去面”的操作后，其二维图形的俯视图如下：
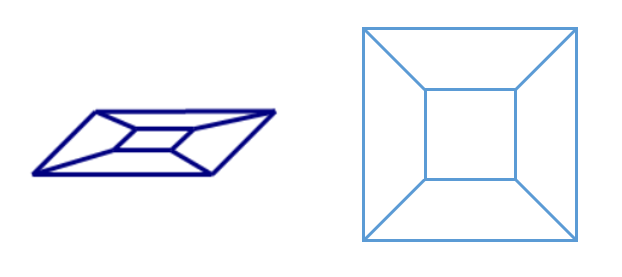这时我们在图形中加一条棱，图形就变成了如下：
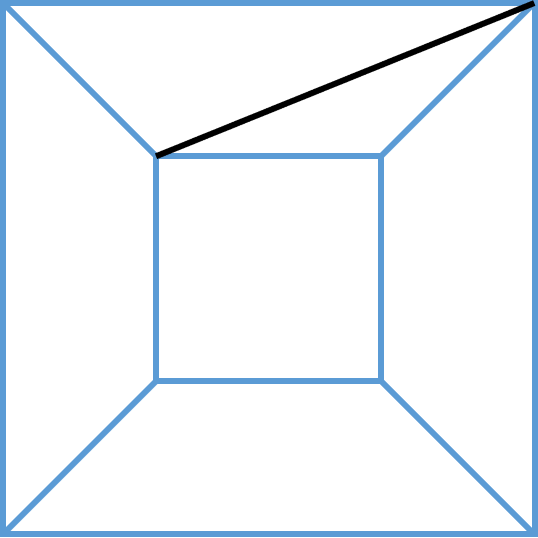
加了这条棱之后，可以发现最上面的区域被一分为二，因此对于整个图形来说，其面数会加一，但又由于其棱数加一，有
因此仍有
3.3 擦边
我们接着对这个图形进行处理，擦除其中一条边，会有什么结果？
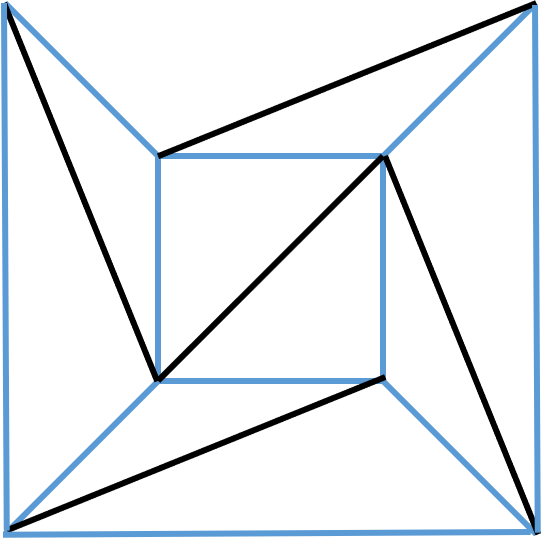
还是和刚才的分析方法相类似，在擦除一条边之后，其面数就会减一，又由于“擦边”使得棱数也减一，因此有
通过一系列“擦边”，图形会变化成一个“飞镖”的样子：
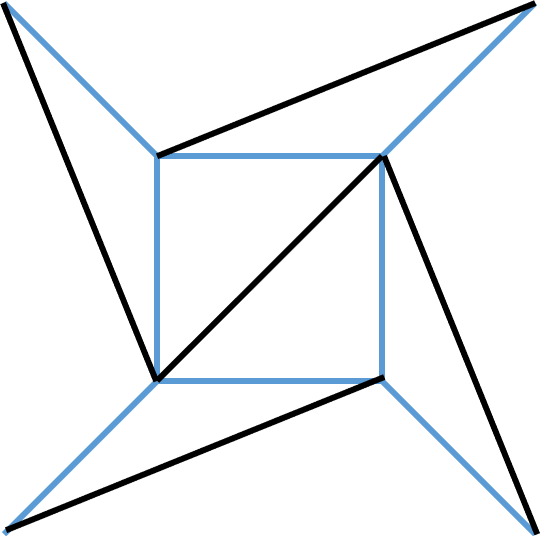
3.4 去角
接下来就是最神奇的一步，擦去这个图形中的某个角，看看会发生什么！
擦去一个角，其面数会减一，其棱数会少二，其顶点数会少一，即
因此对于
来说，其值仍然是不发生变化的！
即有
“擦角”仍然不会使
的值改变，那我们就放心大胆地擦吧！
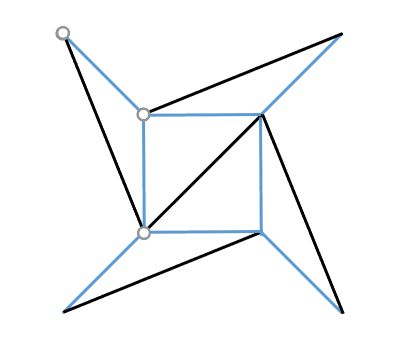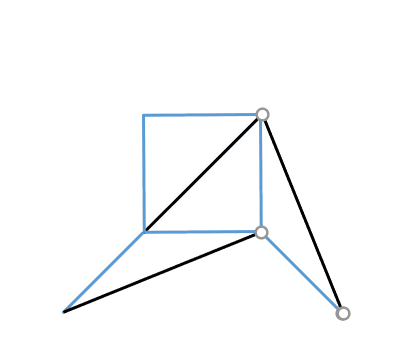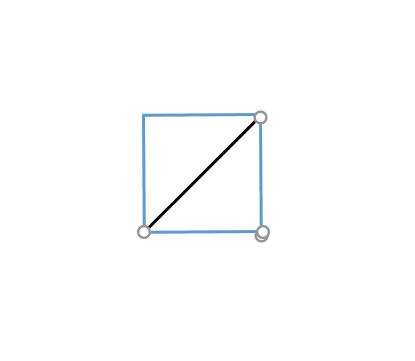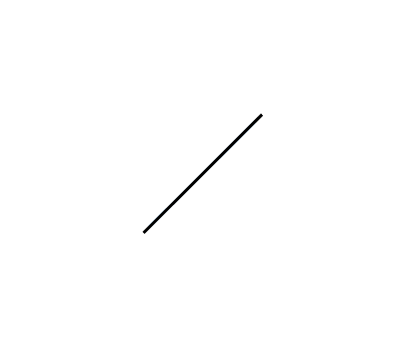
最终，图形会变为一条线段。
我们在初中就知道，线段是一个一维图形，只有两个端点一条线，因此有
