来自:
区块链大本营
(微信号:blockchain_camp)
作者:
苏冠通
安全多方计算已经被公认为区块链发展中重要的密码学技术和工具
,其在交易或者合约隐私保护,钱包密钥管理,跨链交易,区块链扩容等问题中都发挥了独有的作用。
然而由于其具体技术涉及诸多密码学算法和数学背景知识,在相应领域学习和开发之初会茫然而没有头绪
。
本文希望以有限的篇幅将安全多方计算的概念相互连接成系统,以便读者快速学习和构建知识网络。同时,对安全多方计算中运用最多的两个分支:「
基于混淆电路的安全多方计算
」和「
基于秘密分享的安全多方计算
」进行介绍。
在安全多方计算(Secure Multi Party Computation)
文章
中,我们已经描述了安全多方计算如何在数据价值和隐私保护的矛盾下提供一种解决方案,以及这个问题是如何被姚期智先生提出,并如何在实际生活中起到作用。
那么在介绍安全多方计算的进一步应用,以及和区块链之间如何巧妙结合之前,
我们单开一个“进程”来深入到安全多方计算技术内部,将其实现技术给出一个简单明了展示
。
通过这些例子我们可以看到安全多方计算与明文计算之间的区别,这种密码学方案如何实现了它声称的功能,不同实现方法之间的关系与区别,以及安全多计算与其他密码学算法之间的关系
。这篇文章会涉及到一定的密码学基础算法和数学内容,但这不会影响理解安全多方计算本身的思想。
安全多方计算的提出
在姚期智先生(Andrew C.Yao)于1982年发表的文章“安全计算协议”一文中,他提到“
两个百万富翁希望知道谁更富有,然而,他们不希望获得关于对方财富的额外信息。他们应当如何进行这次对话?
”。

这个“百万富翁难题”是安全多方计算的一个特例,
一般化的安全多方计算是n个参与方之间的一个交互式协议,n方分别持有数据x1,x2,…xn
,该协议希望在输入之上计算函数y1,y2,…,yn=f(x1,x2,…xn),并使得第i方只能获得yi而不能获得其他信息。
这个定义看起来并不能带来直观的认知,我们不妨换一种思路来思考:
在一个理想的世界(理想世界范式)中,存在一个完全中立,不和任何人合谋的可信第三方,所有人将数据交给他,之后他进行计算并将结果进行对应分配
。这就完成了一次安全计算。
那么在现实世界(现实世界范式)中,安全多方计算协议就是在不存在这个可信第三方的情况下,完成同样的任务。这给人们更简明扼要思考安全多方计算能力与缺陷的参考。
比如,它并不能保证输入方提供了正确的输入,它也不能一般化的隐藏函数f的信息(代码混淆)。但另一方面,能否保证所有参与方都能同时拿到或者拿不到计算结果(公平性),能否保证参与方中有几方合谋或者试图刺探别人的输入信息时,计算依然可以安全进行(鲁棒性),这些问题则是密码学家在构造不同安全多方计算协议时关心的重点。
现实中的协议并不只有一个,也不是完全相同的几种,
而是效率不同,
安全模型不同,实现方式不同的一系列密码学协议
。
这也是安全多方计算最复杂也最引人注目的地方,
本文我们先介绍一下安全多方计算中运用最多的两个分支——「
基于混淆电路的安全多方计算
」和「
基于秘密分享的安全多方计算
」。
基于混淆电路的安全多方计算
姚期智先生在提出问题的文章里已经给出了这类问题的一个解法:
混淆电路(Garbled Cirtuit)与不经意传输(Oblivious Transfer)相结合
。
这种协议主要适用于两方安全计算,现在有很多工作致力于将这种算法扩展到多方(n>2),然而我们将会看到它天然只适合两方,但两方运算已经可以帮我们解决很多具体问题了。
这种技术之所以被称为“电路”,是其首先将需要计算的函数表示为布尔电路,就像现代集成电路中的逻辑一样,
其中的基本单元就是逻辑门,每个逻辑门规定为两输入一输出但可以具有多扇出
(输出可作为下一级多个门的输入)。
如果电路的拓扑关系确定,整体电路的计算可通过按输入输出连接顺序执行来达成。那么我们就将函数的安全多方计算实现具体为一个门的实现,也就是说我们在现实生活中构造了一个可以等效为理想世界的“安全门”,那么我们可以一般化地来对整个电路进行改造。
姚期智先生提供的布尔电路混淆(Garbling)技术同时利用了不经意传输,不经意传输是一个可以独立利用的密码学工具,我们以2选1不经意传输(1-out-of-2 Oblivious Transfer)为例(如下图所示),其核心目的是接收者(Bob)希望获得发送者(Alice)2个信息(m1,m2)中指定的一个(比如mb),但却无法获得另一个的信息。另一方面,Alice无法获知b的具体数值。
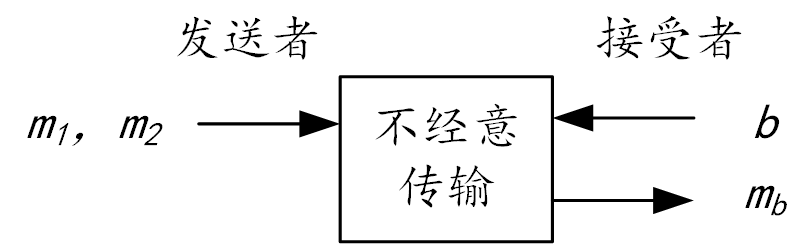
不经意传输
通过上图,我们可以得到一个结论:
任何一个有效的不经意传输协议都代表可以基于其构造一个安全两方计算协议
。
那么我们可以观察这一点如何达成。如果Alice是“电路制造方”,Bob是“电路计算方”,两方想要共同计算f(x,y),其中x来自Alice,y来自Bob。那么Alice负责提供电路生成,不失一般的,我们以一个逻辑与门为例,我们对其每一个线信号(Wire)选定一对密钥
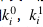 , 分别代表这个信号的0和1。之后,我们利用一个双密钥对称加密函数来获得表1,这个表格即称为一个混淆门。
此时混淆电路完成了构造
。
, 分别代表这个信号的0和1。之后,我们利用一个双密钥对称加密函数来获得表1,这个表格即称为一个混淆门。
此时混淆电路完成了构造
。
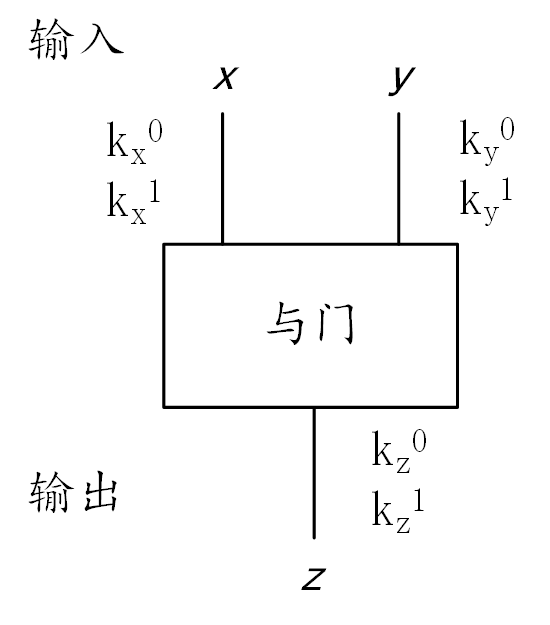
混淆与门示意
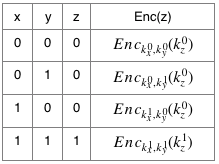
混淆与门对照表
Alice将混淆电路传给Bob,以及x输入对应的密钥值,此时利用不经意传输,Bob可以获得自己y输入对应的密钥值,那么在经历过解密尝试后,Bob获得了对应的结果,在使用满足IND-CCA方案的加密算法时,Bob尝试错误密文的解密时,解密算法会拒绝。
如第一部分所提到的,安全多方计算保证的是一方的输入不会被另一方获得,而不是输入不能被从输出中推断出来。
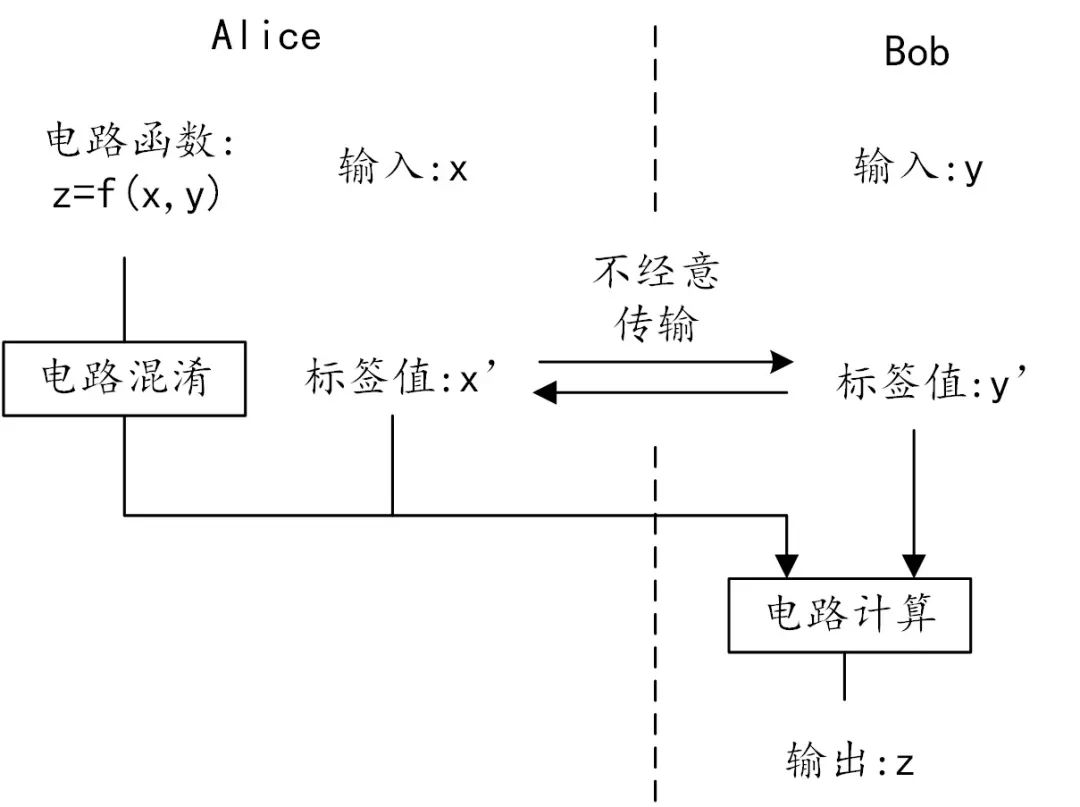
安全两方计算
这就是混淆电路的基本流程。
但这种构造还非常初步和低效
,在这篇文章发布之后,许多改进慢慢被研究工作提出,从安全性,运行效率上都对这一分支的技术有了很大改进,使得实用化变得可行。
这其中比较重要的几个技术包括Free-XOR,Half AND这类减小特殊逻辑门代价的思路,也有Point-and-permute, Row reduction这样降低轮复杂度的算法。
应用上,第一个实现是于2004年发布的Fairplay系统,而2009年Asiacrypt的一篇文章利用混淆电路实现了安全两方计算版本的AES,这使得AES的私钥在计算过程中可以无需恢复,这得益于AES中占大多数的异或门可以利用Free XOR技术降低消耗。
基于秘密分享的安全多方计算
其余的多方安全计算,与两方安全计算不同,都是利用了秘密分享这一技术。这两者之间一个主要区别是,秘密分享中所有参与方都是对等地位的,而混淆电路是区分制造方与计算方的。
此时,输入不是比特值对应的密钥值,函数也不是逻辑电路。输入由参与方之间秘密分享,函数映射为有限域上的运算,这种运算具体化可以由加法和乘法表示,相对于逻辑电路,我们称之为算术电路。
在继续介绍这种方案之前,我们先简单了解秘密分享。
秘密分享是n个参与方将一个秘密s在参与方之间分配的一个密码学工具,常用来保存诸如加密密钥,导弹发射代码等重要敏感信息
。
协议主要有两个函数构成:秘密分发函数(Distribution)与重建函数(Reconstruction)。
分发函数将秘密s拆分成秘密分享值[s]并分发给所有参与方,这一过程一般由s的原始持有方执行。重建函数则允许所有满足重建条件的参与方集合恢复秘密。秘密分享方法于1979年由Shamir和Blakley分别独立提出。我们常用的秘密分享方法之一就是Shamir秘密分享。
1989年,Brickell提出了一般化的秘密分享构造方案,这种构造方法称为线性秘密分享方案(Linear Secret Sharing Scheme)。
这个方案中用访问结构(Access Structure)来约束哪些参与方联合可以重建秘密
。

















