
作者:131v1vv 本文来源于作者EETOP论坛帖子及作者公众号:不忘初心的模拟小牛牛
模拟集成电路中,以OPA或OTA为核心的基本单元构成了功能多样且更复杂的子系统,完成对不同信号处理的需求。
在信号与系统的学习中,对于LTI系统,复杂高阶系统都可以分解为较低阶数的子系统。其中
一阶(First-Order)
系统和
二阶(Second-Order)系统
的时域频域特性是基础内容。
我们知道一阶系统
相对简单,等效使用的也最为广泛。其
时域响应是呈指数形式的,响应速度取决于时间常数(RC),频域仅包含一个极点。二阶系统相对复杂一些。复杂在其时域响应会根据系统参数的差别而表现出不同的形式。常见的OTA,都需要等效为二阶系统。那么为了保证系统
有足够的的稳定性
(鲁棒性),就引入了
补偿
的概念。
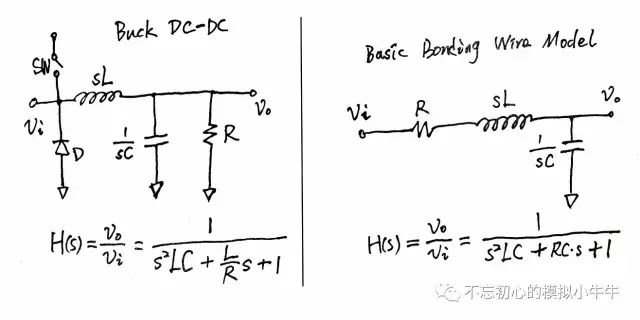
图1
这里举了两个二阶低通系统的例子,图1左为降压型(Buck)开关电源的负载端电路结构,其传递函数就是二阶的;图1右为芯片简化的焊接线模型,其传函也是二阶的。
低通二阶系统的传输函数,可以方便地表示为如图2所示的形式。

图2
极点的位置随阻尼因子变化如图3所示。当阻尼因子大于等于1时,有两个实根。
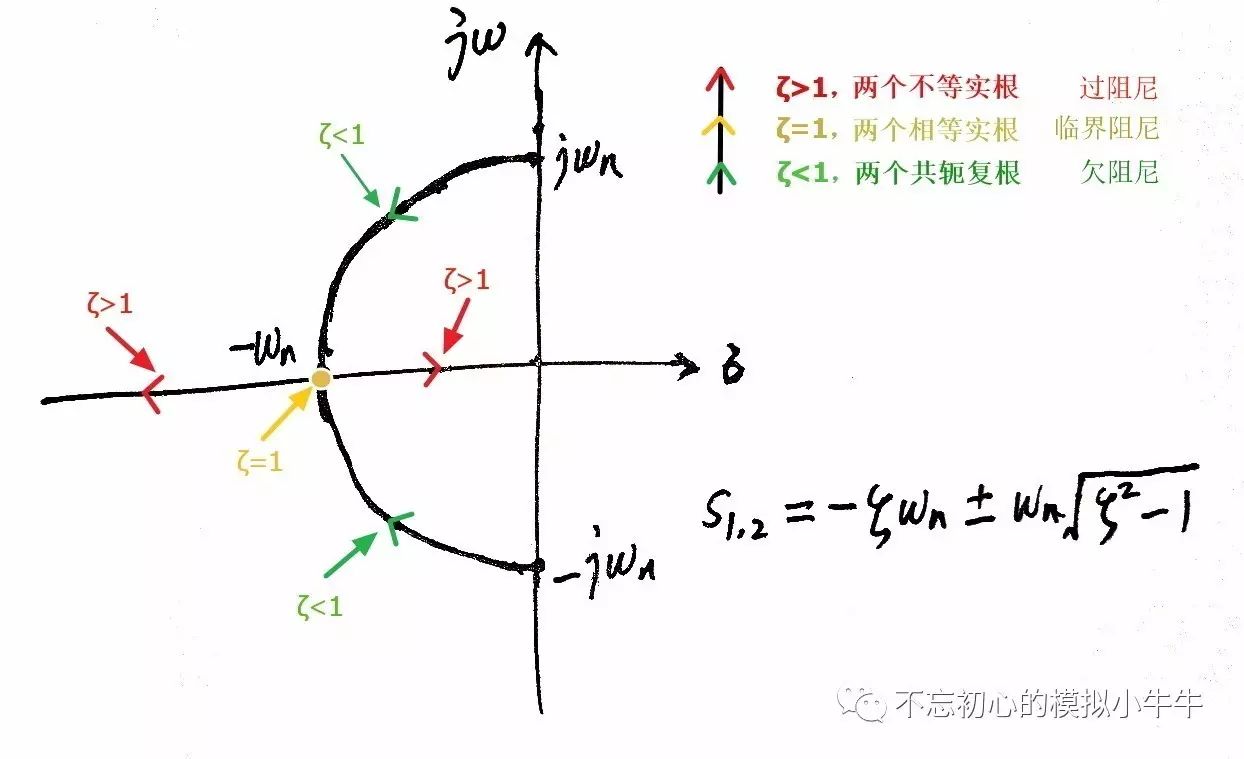
图3
对图2所示的
传输函数
归一化后,幅度频率和相位频率关系如图3所示。
。当阻尼因子
ζ<0.707
(1/√2)时,其频域响应存在
过冲
。过冲的尖峰
相对
位置
和
尖峰值M
p
也和阻尼因子有关。

图4
幅度频率特性和阻尼因子的关系示意图如图5所示。
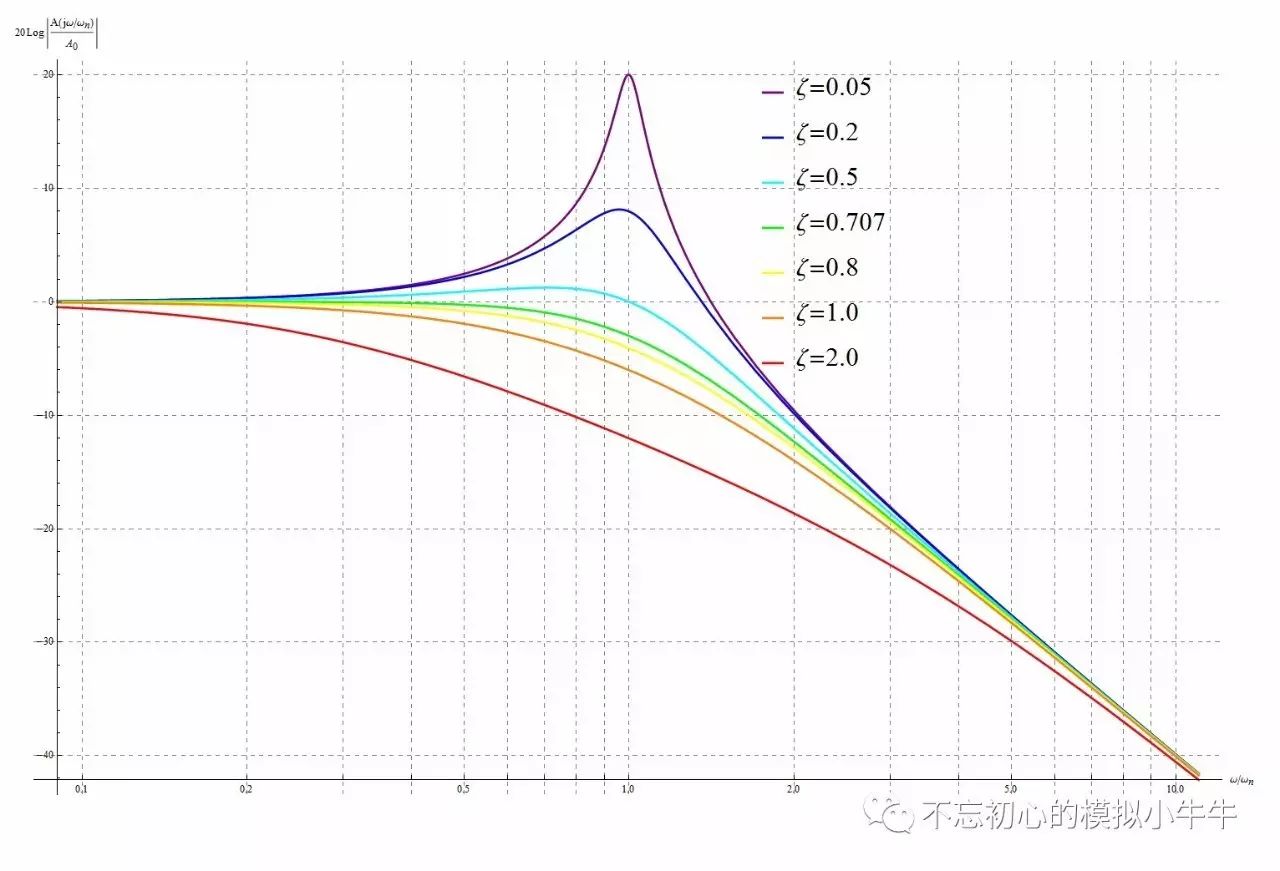
图5
当阻尼因子
ζ<0.707
,
频域响应
尖峰值M
p
及其
相对位置ω/ω
n
和
阻尼因子ζ
的关系如图6所示。

图6
阻尼因子ζ
对
相移频率特性影响
如图7所示。
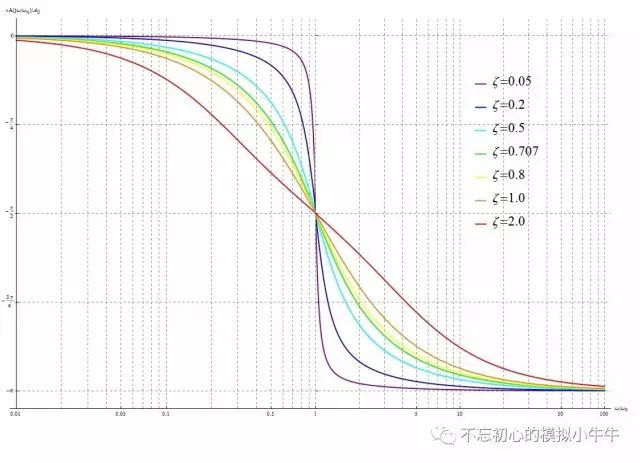
图7
结合图5和图7,可以看到欠阻尼下,其作为低通的频率选择更接近
理想低通滤波器
特性。缺点是在频域幅度响应会出现尖峰,该尖峰也会表现在时域特性中。
图8是我们对一个系统的常规理解,包含了时域、频域及其转换关系。从不同的维度可以更全面、更深入的了解一个系统。对于二阶系统,我们也可以试着从这些方面同样进行分析。
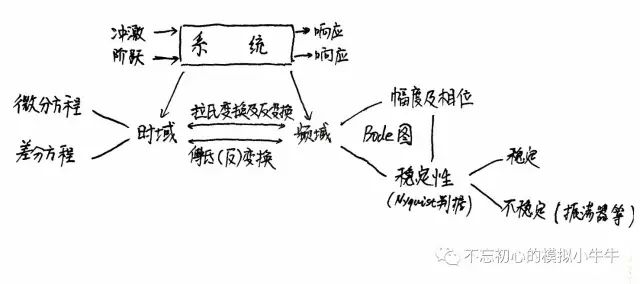
图8
本期内容就先到这里,后续我们接着分析三种阻尼情况下其时域的响应特性。
第二期
这次我们从时域角度,回顾不同阻尼因子下二阶系统的冲激响应和阶跃响应,公式会比较多。
冲激响应
我们知道系统函数是系统对单位冲激响应的拉普拉斯变换,通过拉普拉斯反变换,就可以得到不同阻尼情况下的单位冲激响应了。
二阶系统的幅频响应如图1所示。两个根和阻尼因子有关。
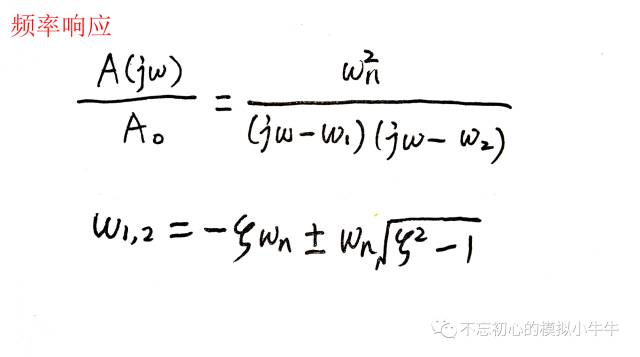
图1
不同阻尼因子时,系统函数的根形式如图2所示。
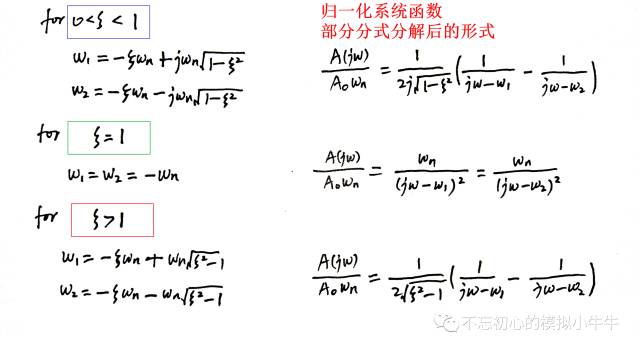
图2
冲激响应时域表达式如图3所示。可以看到当
0<
ζ<1
时,其瞬态响应包含了正弦项,也就是冲激响应存在振荡。
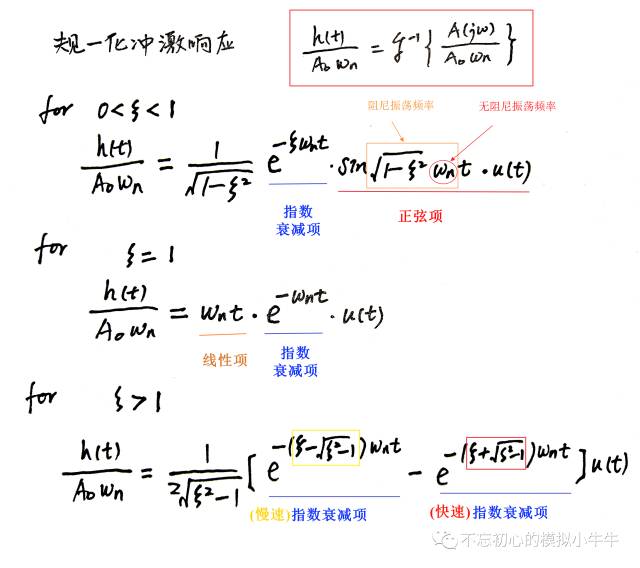
图3
不同阻尼因子归一化(
相等
ω
n
条件
)后的冲激响应如图
4所示。横坐标为
ω
n
t
,纵坐标为
h(t)/(
ω
n
A
0
)
。
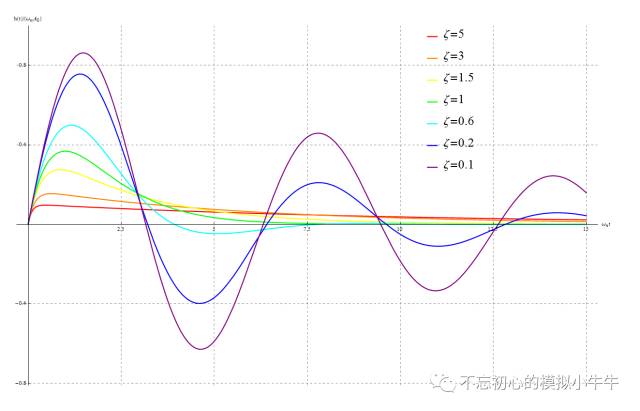
图4
阶跃响应
当输入信号为单位阶跃时,系统的输出为阶跃响应,通过求拉普拉斯变换及反变换,可以求得其时域的阶跃响应。同样也可以使用单位阶跃输入信号和冲激响应求卷积得到阶跃响应。
当阻尼因子
0<
ζ<1
时,其阶跃响应瞬态分量包含了指数项和正弦项,指数衰减受阻尼因子影响,阻尼因子
ζ越小
,指数衰减速度
越慢
。正弦项的角频率也称为阻尼振荡频率,阻尼因子
ζ越小
,阻尼振荡频率
越高,
也越接近无阻尼振荡频率或自然频率。
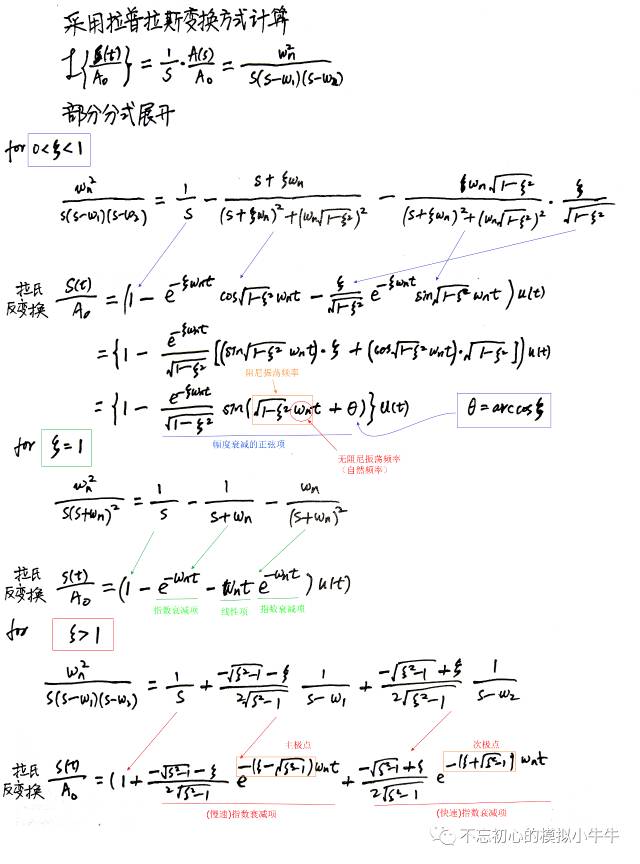
图5
当阻尼因子
ζ=1
时,其阶跃响应瞬态分量包含了指数衰减项,线性项和指数衰减项乘积。其瞬态响应
无超调量
。
当阻尼因子
ζ>1
时,其时域表达式包含了两个指数衰减项,其中主极点
ω
1
为慢速衰减项,主极点决定的瞬态分量,持续时间长,初始幅度大,在系统响应中起主导作用。次极点
ω
2
为快速衰减项,其瞬态分量持续时间短,初始幅度小,在系统响应中起辅助作用。
不同阻尼因子时,其归一化后阶跃响应如图6所示。横坐标为
ω
n
t
,纵坐标为
s(t)/A
0
。
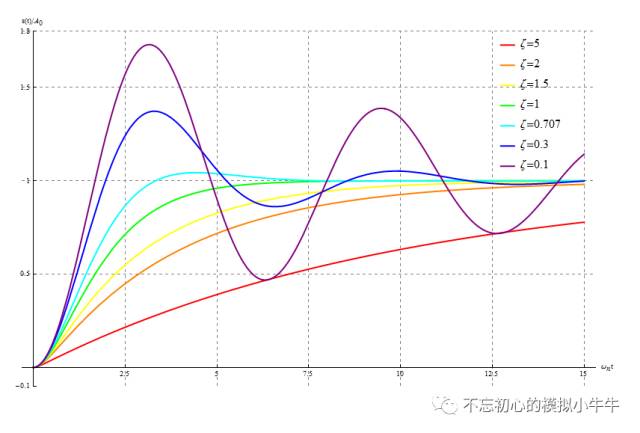
图6
我们可以看到,在阻尼因子
ζ<1
时,阶跃响应存在超调量,但其瞬态响应有比较短的建立时间。过阻尼条件下,虽然无超调量,但建立过程比较慢。尽管有些系统中可能确实要求不能存在过冲情况。但大部分系统中为了追求比较快的建立,还是在系统设计中故意把阻尼因子
ζ
设计的
稍微
小于1
。这也是二阶系统设计阶段需要
折衷
的地方。
这期我们先聊这么多,下一期,我们考虑模拟集成电路中由负反馈构成的二阶系统的一些结论。
第三期
接上期分析,对于欠阻尼情况
0<
ζ<1
,其瞬态响应存在的过冲归一化峰值时间及超调量如图1中公式所示,结果如图2所示。

图1
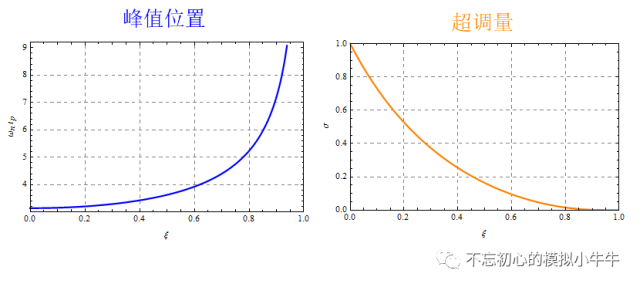
图2
在模拟电路中,经常使用的负反馈电路,需要考虑负反馈系统的稳定性。这里需要综合考虑放大器的主极点和次极点及反馈系数构成的负反馈系统是如何影响二阶系统的阻尼因子的。

图3
对于图3的所示的负反馈系统。前置放大器包含了主极点
ω
1st
和次极点
ω
2nd
,其传递函数表示为y(s)。假设反馈系数β,频率特性无相移。系统
闭环响应A(s)
如图4所示。低频增益表示为A
0
,频率响应表示为之前讨论的二阶系统的标准形式,可以得到无阻尼振荡频率和阻尼因子和前置放大器及反馈系数的关系。

图4
为得到图3系统的相位裕度,这里先得到环路增益(Loop Gain)的表达式,如图5所示。

图5
环路增益的幅频特性曲线穿越0dB(单位增益)的频率定义为穿越频率
ω
c
(Cross Frequency),如图6所示。

图6
穿越频率和无阻尼振荡频率比值和阻尼系数的关系可以用图7表示。
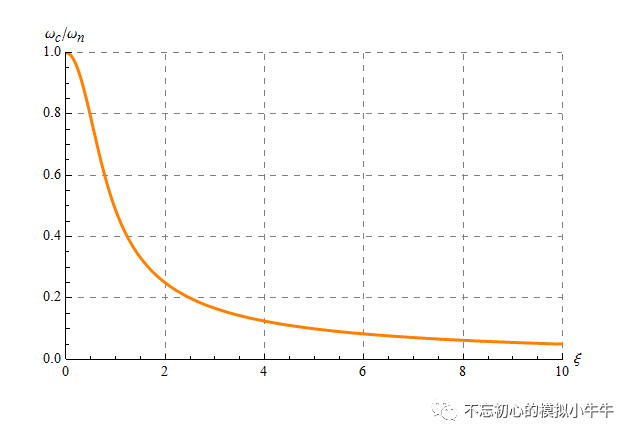
图7
相位频率表达式和相位裕度表达式如图8所示。

图8
相位裕度和阻尼因子的关系如图9所示。
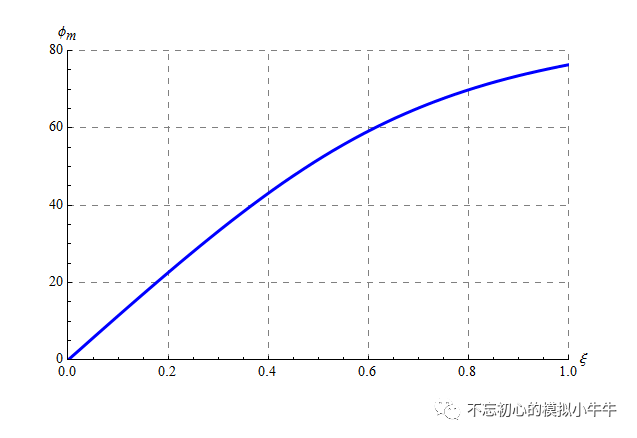
图9
我们看到,时域角度,超调量归一化峰值时间等,频域角度,穿越频率,相位裕度都和阻尼因子有关。这里把这些图汇总一下如图10所示。
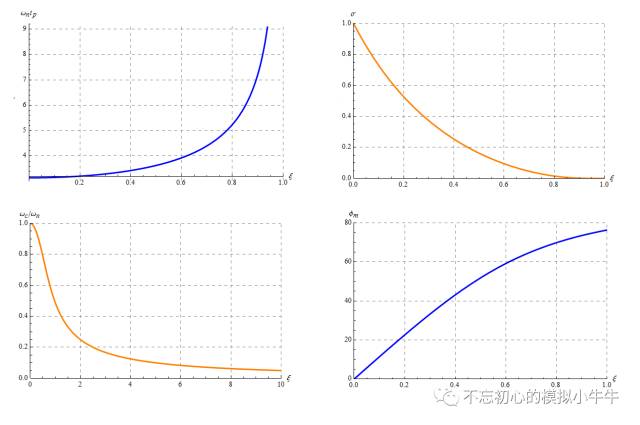
图10
通常,我们会通过时域的阶跃响应的过冲情况估算出阻尼因子,通过阻尼因子和相位裕度的关系,得到对应的相位裕度。这两者本质上是一致的。
通过3期的内容,相信大家会对二阶系统有比较系统,完善的回顾学习。其实,还有一点,就是运放次极点位置和GBW的相对位置,对PM的影响。这个我准备再补充一下,争取能更全面的把这部分内容融汇贯通。
好啦,这期就到这里了,下期见吧。
第四期
这期内容会稍多一些,我们先来划重点。围绕以下几个问题,我们逐条分析回答。
1、次极点和GBW相对位置对相位裕度的影响?
2、固定GBW,次极点位置对阶跃响应速度的影响?
3、举个小例子吧。
对于第一个问题,
我们先思考一下单极点构成的闭环系统,如图1所示。这里增益带宽积GBW=
y
0
ω
1st
,(
后续如无特殊说明
,
GBW为rad/s的形式,注意Hz表示时的2Pi转换关系
)。根据增益带宽积恒定的结论,当反馈系数为β时,有低频闭环增益约为1/β,闭环带宽约为βGBW,穿越频率也约为βGBW。这里不考虑反馈系数的频率特性,认为随频率变化恒定。
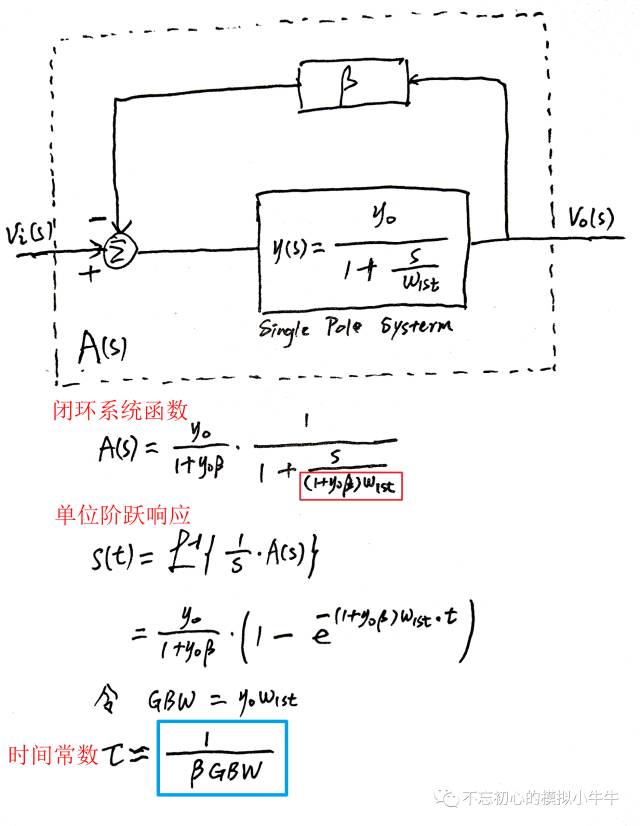
图1
图1所示的单极点闭环系统,由于环路增益(Loop Gain)仅包含一个极点,所以相位裕度为90度。
如果放大器是两个极点的形式(主极点
ω
1st
和次极点
ω
2nd
)。其闭环响应的形式和阻尼因子、无阻尼振荡频率关系如图2所示。有直观理解,如果存在次极点在穿越频率处,相移应该为-135度,相位裕度近似为45度。是需要稳定性考虑的情况。
图2中定义了次极点
ω
2nd
和GBW的位置比例关系
k
,则无阻尼振荡频率,阻尼系数都可以表示为含有GBW、k和β的表达式。
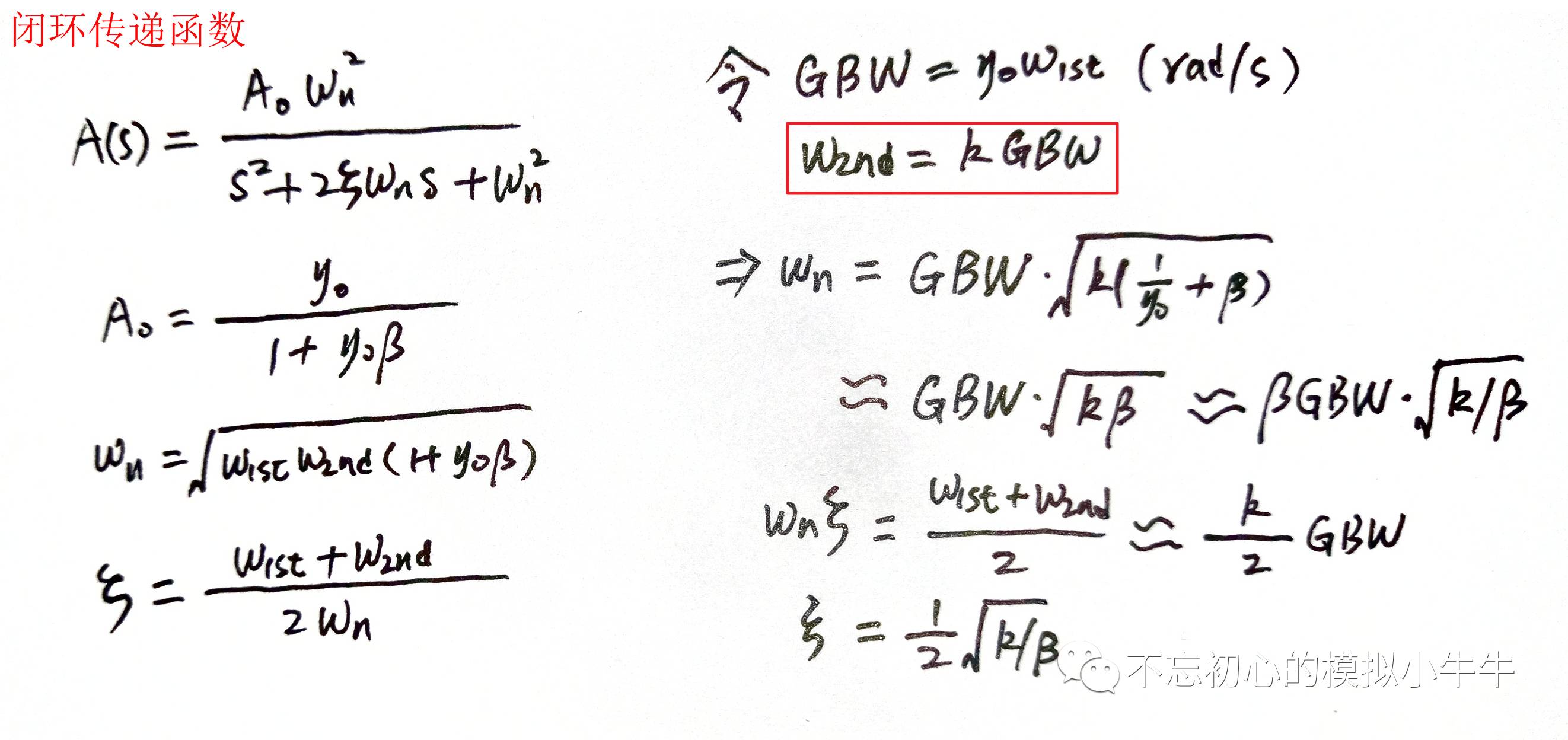
图2
图3给出几种不同反馈系数
β及次极点不同位置关系
k
时,阻尼因子的变化情况。其中k/β=4
时,有
ξ=1,是临界阻尼情况。时域响无过冲。当k/β=2
β
时,阻尼因子ξ=0.707,频域响应无尖峰。
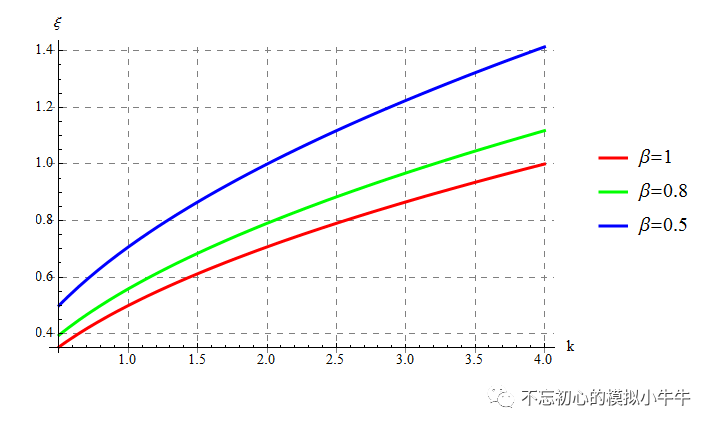
图3
同样对于不同的反馈因子
β和次极点位置比例
k
,可以得到穿越频率
ω
c
和对应的相位裕度
Φ
m
与k/
β关系的表达式,如图
4所示。
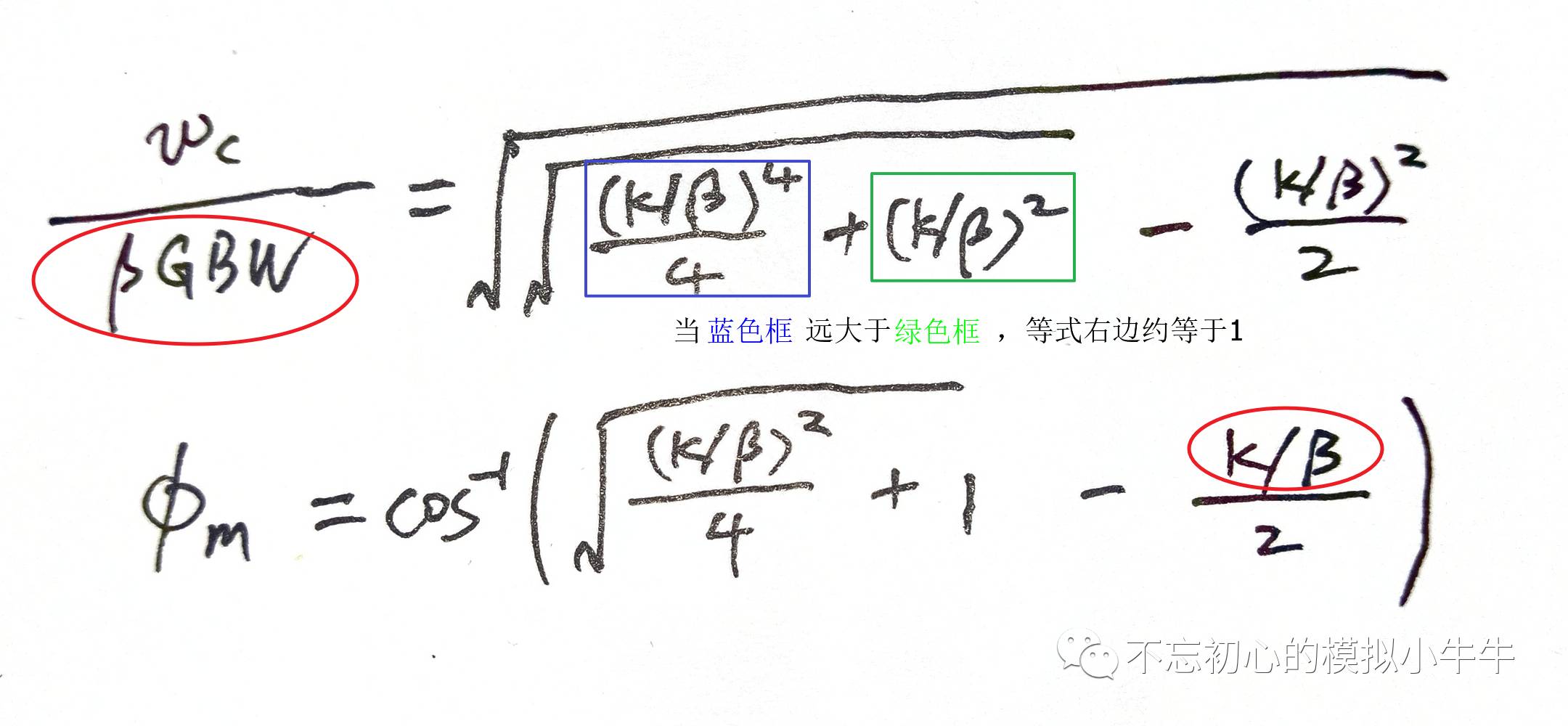
图4
对于穿越频率表达式,绘制几种情况如图5所示。当次极点远离GBW时,也即k值较大,穿越频率即为闭环带宽
βGBW
(
相当于单极点系统中,闭环增益为1/β的-3dB带宽
)。当次极点越接近
βGBW
时,会比较明显的影响到穿越频率的实际位置。也即
较低频率的次极点的存在使得穿越频率提前
(小于
βGBW
)。
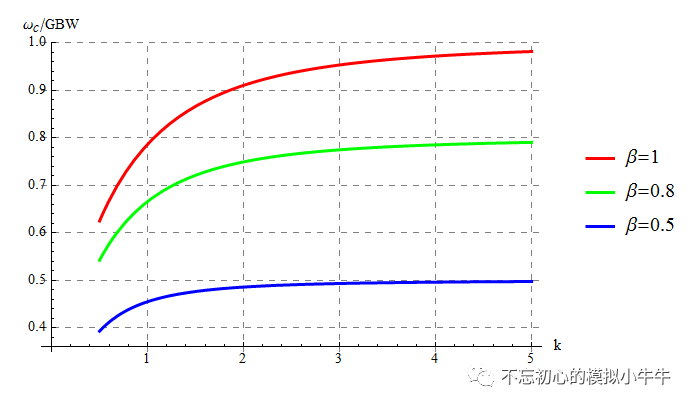
图5
这里同样绘制得到相位裕度
Φ
m
,
如图6。当次极点越靠近GBW时,相位裕度也越来越小。其中
β=1时,次极点位于GBW处(k=1),有相位裕度约为
52
度。这是由于次极点的存在导致穿越频率比GBW小,注意这比直觉的
45
度相位裕度要大一些。原因也是因为次极点的存在使穿越频率提前(更低)。
这也要求我们在实际设计Opamp或OTA时,要注意控制次极点的位置。从而留足够大的相位裕度,保证时域有比较好的瞬态响应。
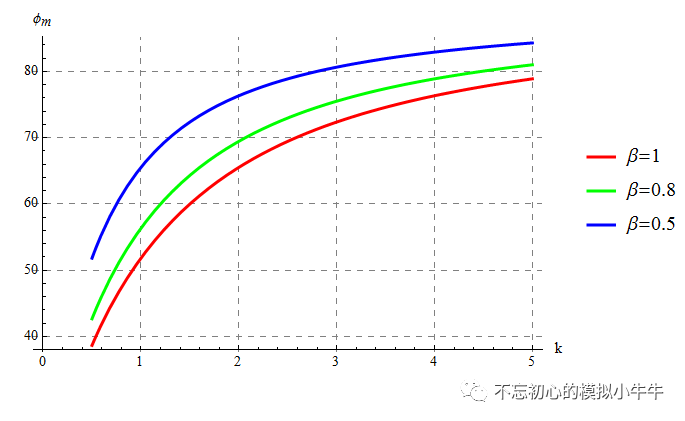
图6
所以,这里也就可以回答第一个问题了,
对于固定的GBW,把次极点位置推离GBW频率处,可提升相位裕度。当次极点位置超过2
β
GBW
时,阻尼因子大于0.707,频域闭环响应无尖峰。当次极点位置超过4
β
GBW
时,阻尼因子大于1,时域响应无过冲。
对于第二个问题,时域响应到底和什么有关呢?容我慢慢解开其面纱。
这里我们还是先回顾图1所示的单极点闭环系统。可以看到,如果放大器只有一个主极点
ω
1st
,有闭环带宽约为
βGBW
,也等于其时域阶跃响应的时间常数1/τ。
我们知道,对于一阶系统阶跃响应有如下的几个关系。4.6t和7t是个高精度的建立标准。注意,图7右的信号为占空比50%的方波。可以看到,如果信号频率为闭环带宽的一半时,可以达到0.2%的精度。
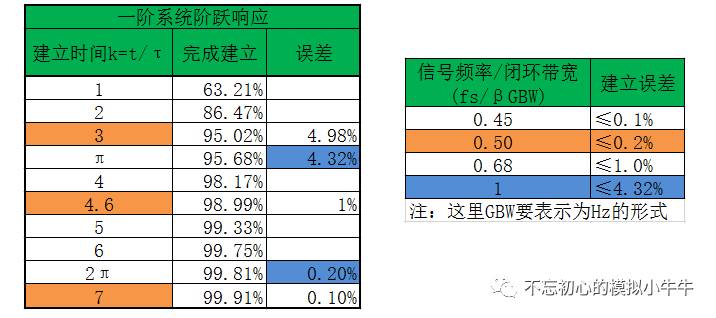
图7
回忆先前的假设,
GBW保持不变
,关注次极点
ω
2nd
和GBW的位置比例关系k。图8上,我们重新给出了阻尼系数和
k/
β
的关系。其中
k/
β=4
是临界阻尼。
图8下,给出了
k/
β>4
时,两个实根(
ω
1
闭环主极点
,ω2
闭环次极点
)的轨迹。其中当k较大时,闭环主极点
ω
1
趋向于
-
βG
BW
,也就是次极点频率较高时,可以看做闭环带宽为
βGBW
的单极点系统。
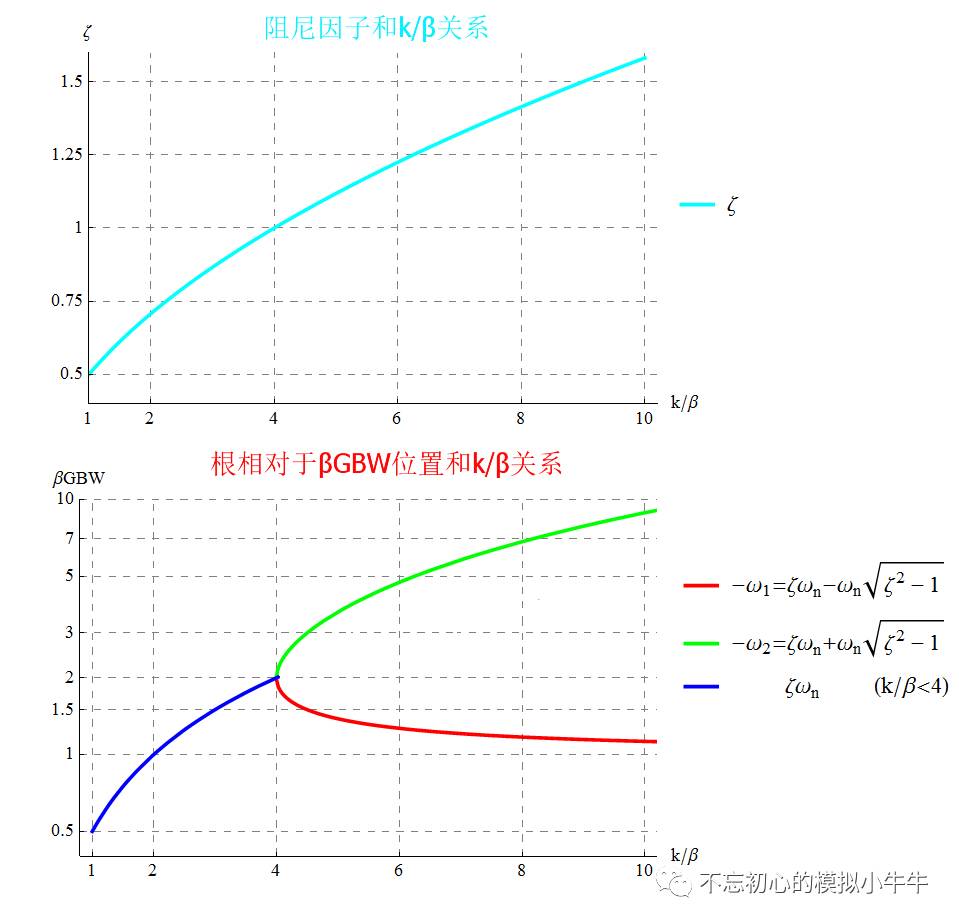
图8
也可以看到,当次极点接近4
βGBW
,闭环主极点和次极点开始相互靠拢接近,并收敛到二重实根2
βGBW
,达到了峰值。之后随着
k/
β
进一步减小,闭环系统进入欠阻尼状态,其根实部如蓝色所示。这些表现在时域会是个什么效果那?
重写阶跃响应的近似表达式,如图9所示。其中参数为
k/
β
,时间单位为
βGBWt
。

图9
绘制阶跃响应如图10(a)所示,这里固定
β
GBW,得到不同次极点位置及反馈系数情况下,和比值k/
β的关系。
建立接近完成的细节如图(b),可以看到k/
β
=4,也就是绿色线,是临界阻尼的情况,也是无过冲情况下最快的建立。当k/
β
<4时,欠阻尼下,存在时域过冲,不过建立会更快一些(更早到达稳态值)。具体还是要看应用场景吧,允不允许过冲存在。
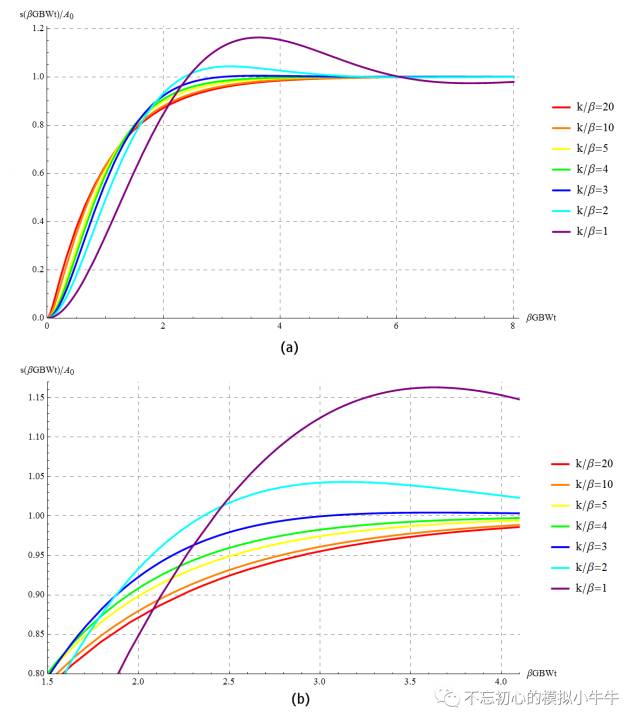
图10
这里补充一个时域过冲的超调量
σ
和频域相位裕度
Φ
m
的对照关系,如图11。大多数时候还是会通过时域过冲的超调比例来进一步验证相位裕度是否充足。有几个特殊点,如阻尼因子ξ=0.707时,相位裕度为
65.5°
,超调量为
4.3%
。更多数据可以查看封面的结果。
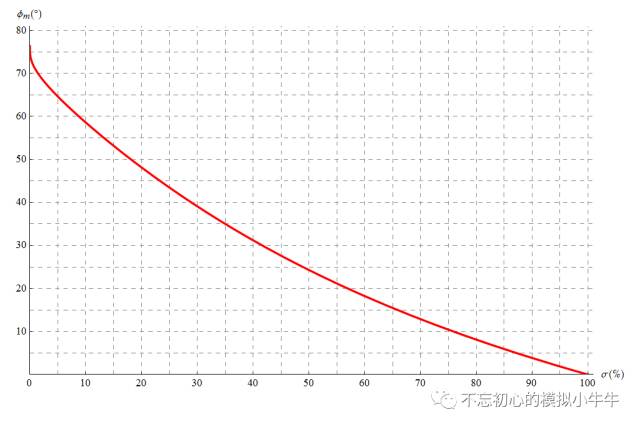
图11
最后举个例子吧,对于单级驱动容性负载的OTA,可以认为主极点就在输出端,如图12(a)。这里为方便,反馈系数
β=1
,Buffer连接形式。一个典型的应用场景就是通过Buffer测试芯片内部的方波(或其他变化)信号,负载为
空载或示波器探头的容性负载
。为了减小Buffer引入的误差,对该OTA的要求包含了低频增益Dc Gain和增益带宽积GBW,设计时可以根据允许的误差范围和输入信号频率,合理分配静态和动态误差的贡献比例。
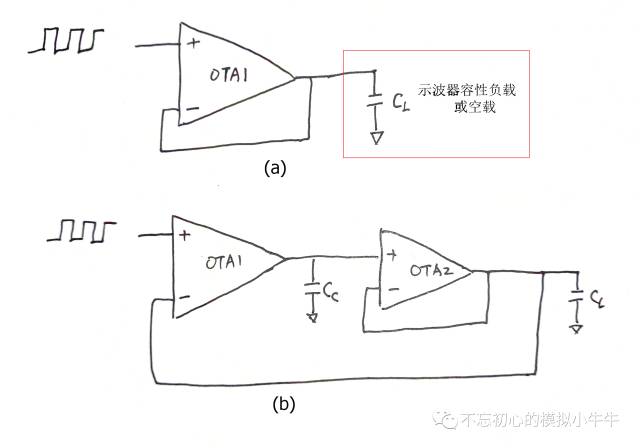
图12
更改一下结构,如图12(b)。OTA1保持不变,在OTA1和负载电容
C
L
中间插入Buffer连接的OTA2。那么如果图(a)和图(b)输入信号一样,该如何设计
OTA2
及电容
C
c
。
这里OTA1、OTA2、
C
c
和
C
L
构成了二阶放大器,系统总的为Buffer连接。为了保证空载时(
C
L
=0
)的稳定性,图12(b)中
C
c
处形成的极点通常作为
主极点
。那么OTA2的输出端电容
C
c
的极点就是
次极点
了。
电容Cc:
为保证图12(b)能和图12(a)能够Buffer相同速度的输入信号。电容Cc应该小于等于CL。这样能够保证整个环路的
GBW
1
大于等于图12(a)中的。
OTA2考虑:
OTA2的Buffer连接,从频域可以看做为单位增益,主极点为OTA2的增益带宽积
GBW
2
的低通单极点子系统。这里就要考虑重载(
C
L
=示波器探头的容性负载
)时,OTA2的
GBW
2
和系统闭环带宽
GBW
1
(
βG
BW=
GBW
1
)的位置关系。比如满足
GBW
2
>=
4
GBW
1
,保证时域无过冲。或者激进一些满足
GBW
2
>=
2
GBW
1
,保证较快的响应速度,及
OTA2
较低的功耗。
注意OTA2按照重载设计。空载时,次极点位置在更高频率处,可以有更大的相位裕度。
好了,本期的内容就这么多了,二阶系统我们也算把相关内容都汇总在一起了,希望通过对基础理论的温习,进一步思考,指导我们的模拟电路设计。
为了更好地便于大家交流学习,EETOP按区域组建了一些微信群,欢迎所在区域的网友加入各自的区域群,加群方法:
先加 jack_eetop 为好友,发送如下信息:
加群+区域+单位(或院校)+职业
。如果加入的是以省为单位的群,则需按以下格式发送加群信息:
加群+省名+城市名+单位(或院校)+职业
比如: 加群+北京+利达科技+数字IC设计
加群+浙江+杭州+xxx公司+xxx设计
目前先开通如下7个区域群,欢迎对号入座。
长按二维码,加群主为好友,拉你入群

EETOP北京群 EETOP苏州 EETOP上海 EETOP深圳
EETOP成都 EETOP西安 EETOP浙江
此外,我们也会陆续开通一些行业群,现已开通:
EETOP汽车电子 ,
EETOP GPU&深度学习
,
EETOP 物联网
欢迎业内人士加入
请按如下格式填写:加群+物联网(或 GPU等)+单位
加群前请务必在朋友圈分享至少一篇EETOP的微信文章
 点击阅读原文前往论坛查看原帖
点击阅读原文前往论坛查看原帖




