不管你信不信
反正我信了
###贝特朗箱子悖论
我有三个箱子，每个箱子都有两个隔档。
第一个箱子里面是两块金条
第二个箱子里面是两块银条
第三个箱子里面是一块金条和一块银条
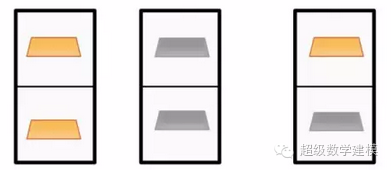
你随机抽取一个箱子，然后随机打开一个隔档。
如果里面是金条，那另外一个隔档里是金条的概率是多少？
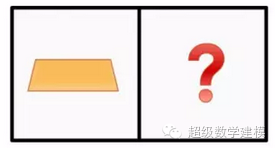
你的第一反应一定是：1/2
因为只有两个箱子里面有金条，你就想，我一定选中了其中一个。
又因为其中一个箱子里面是一块金条和一块银条，所以，另外一个隔档里面是金条的概率就是1/2.
对吗？
你错了！
实际上比那要复杂得多。要推算出为什么不是1/2，让我们给金条和银条贴上标签：
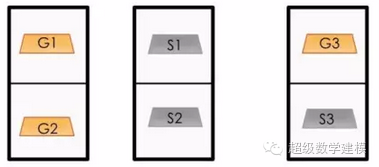
然后，我们列举了一下所有可能抽取到的情况：
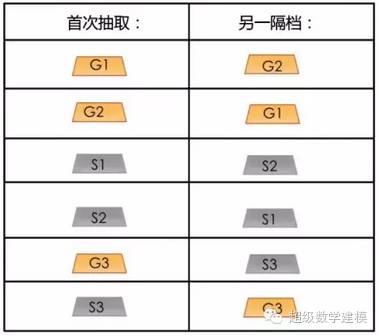
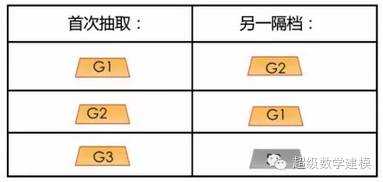
接下来，让我们只看一下第一次抽到金条的情况：
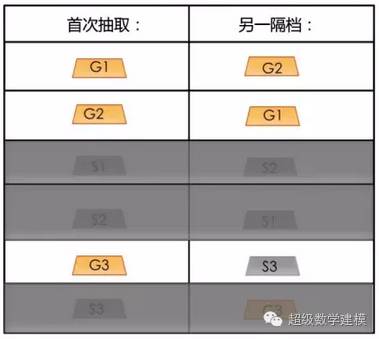
所以，如果你第一次抽到的箱子里有一个隔档是金条的话，那么另一个隔档里是金条的概率是2/3.
3次中有两次另一个隔档是金条，是因为在你抽到的3次金条中，有两次你分别抽到了G1和G2.
3次中有一次另一个隔档是银条，是因为在你抽到的3次金条中，有一次你抽到了G3.
这个问题和三门问题有非常紧密的联系。
###如何用一块镖板推算出圆周率π
你可以用有块镖板推算出圆周率π的值
有一种很有趣的方法，通过反复随机在正方形镖板内选点，可以推算出圆周率π的值
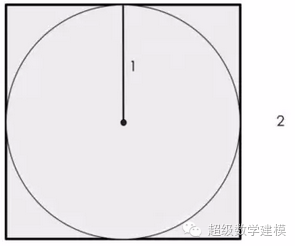
首先，我们需要做一些运算：
正方形内切圆的半径为1，正方形的边长就是2.
那么，圆的面积就是：
πr²=π（1²）=π
正方形的面积就是：
2²=4
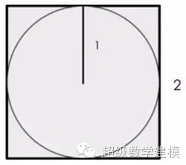
接下来，我们在正方形内随机选取几千个点。
有一种很有趣的方法，通过反复随机在这个正方形内选点，可以推算出圆周率π的值。
选的点越多，得出来的结果就越接近。
选点结束后，将结果带入下面的公式，就可以推算出π的值：
这是运用几何学和概率推算圆周率π的方法。
###调和级数发散至无穷大
下面就是调和级数：
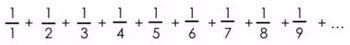
分母持续增长趋向无穷大。
许多其他的无穷级数都聚合至单个数字：
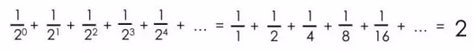
然而，调和级数却不是这样：
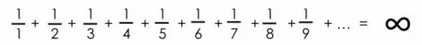
对于大多数人来说，这是非常非常难以理解的——
请看下面：
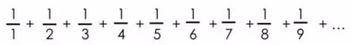
它看起来增长的越来越慢！看那分数的值多小啊！而且只会越来越小！
但实际上，调和级数不会聚合到单个数字。它在趋向无穷大，只是很慢很慢。
我们来证明一下。
证明调和级数是发散的——
让我们把调和级数和另外一个小一些级数对比一下：
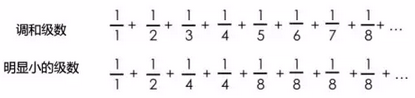
注意，从第二项开始，第二个无穷级数中的每一个数都比调和级数同一位置的数要小。所以：
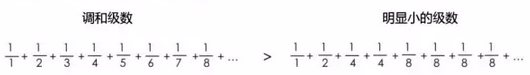
但是我们看一下第二个无穷级数：
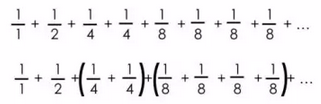
可以简化为：
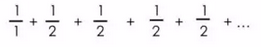
很明显可以发散至无穷大：
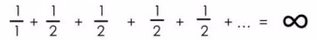
所以，如果
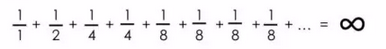
并且
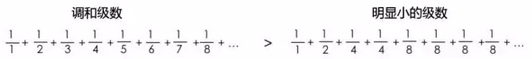
那么
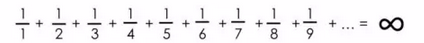
###你的朋友很可能比你人缘好
从数学上讲，大多数人的朋友平均所拥有的朋友数量要比他们自己的朋友多。
这种很有应用题色彩的现象，很大程度上是由于社交网络的数学性质所决定的。
它基于这样一种理念，那就是平均来讲，大多数人的朋友都拥有比他们自己更多的朋友。
社会学家斯科特·L·费尔德在1991年的一遍论文中，发现71%的人平均所拥有的朋友都比
他们的朋友所拥有的朋友要少。
关键点在于人缘好的人。
我们来看一个例子。
我们再来回顾一下你的办公室来证明这一点（现在经过裁员，只剩下20个人了）。下面是你办公室的朋友关系图。连接线表示他们之间为朋友关系：
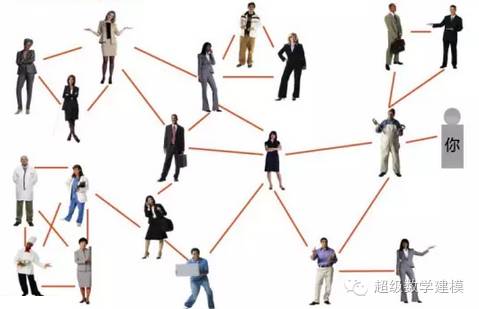
在这个办公室里，平均每个人拥有2.85个朋友。
但是，每个人的朋友却平均拥有3.39个朋友。
图中标注出了拥有朋友数量高出平均数的人。他们都是人缘极好的人。更重要的是，办公室的20人中有17人至少跟她们中的一位是朋友：
这只是一个例子，但在现实世界中却稀松平常。
在推特上，在微博上，脸谱、人人......你所关注的人很可能拥有比你更多的粉丝。
基本上讲，相对于朋友较少的人，你更愿意与朋友多的人成为朋友。
这条规则不仅仅适用于朋友关系。
###任意四边形边线中点连线构成平行四边形
画一个四边形，可以是任意古怪的形状，不规则四边形、凹四边形、凸四边形......只需要四个点和四条直线。
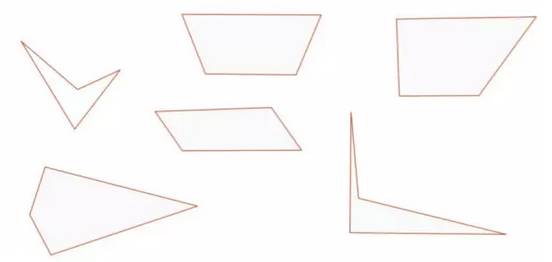
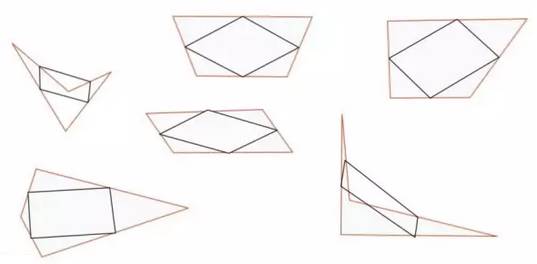
标出每条边线的中点
将边线相连。你总是会得到一个完美的平行四边形。
###三个犯人
三个犯人都住在隔离间，并且都被判处了死刑。狱官随机赦免了其中一个犯人。看守知道谁会被赦免，但不会说。
犯人A脸皮厚，让看守告诉他，B和C谁会被执行死刑。
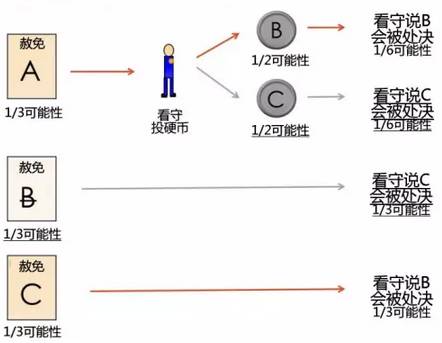
如果赦免的是B，那就说C；如果赦免的是C，那就说B；如果B和C都没被赦免，那就投硬币决定说谁。
看守告诉A，犯人B将会被执行死刑。
犯人A兴奋不已，觉得自己生存的机率从1/3提升到了1/2，因为原来是A、B、C三个人有一人被赦免，现在是A、C两个人有一个被赦免。
A将此告诉了C，C同样兴奋不已。他的理由是：A生存的机率仍然是1/3，而C却有了2/3的机率被赦免。
谁错了呢？
答案是：犯人C是对的。
最初，三人都有1/3的机率被赦免。看守说B会被处决，这意味着一下两者可能：
--C会被赦免（1/3的机率）
--A会被赦免，投硬币投到B（1/6的机率）
这就意味着A被赦免的机率是C被赦免的一半，二B已不可能被赦免。
所以，A被赦免的机率没有变化，仍然是1/3.而C被赦免的机率已翻倍至2/3.
如果你仍然怀疑，那我们就对这其中的机率进行一下盘点：
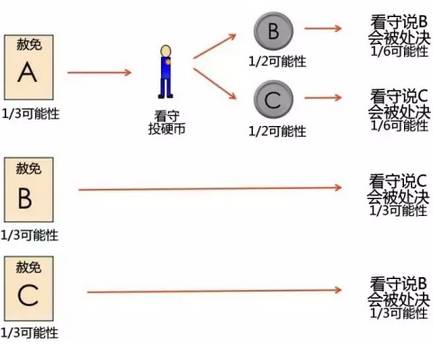
接下来，我们只看B被处决的情况。我们看到，C被赦免的机率是A的两倍。
既然我们知道，现在B被赦免的机会为0%，并且，C被赦免的机率是A的两倍：
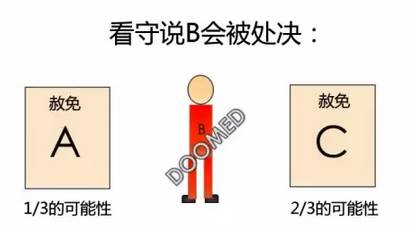
可见，犯人A问了多么愚蠢的一个问题。
主编圈点：这些问题是不是和我们平时所理解相悖呢，事实就是如此，你明白了么。
往期精彩回顾
1.未来十大趋势，你准备好了没？
2.涨见识的动图（化学反应如此有趣）
3.数学系和物理系的学生有什么差别？
4.你知道到底是什么导致我们近视的吗？
5.300年后的人类，看完直接目瞪口呆！
6.没有牛顿、爱因斯坦，物理学将会怎样？
7.你问探索太空有何用
本期编辑|七彩石头
环球物理，以物理学习为主题，以传播物理文化为己任。专业于物理，致力于物理！以激发学习者学习物理的兴趣为目标，分享物理的智慧，学会用物理思维去思考问题，为大家展现一个有趣，丰富多彩的，神奇的物理世界！
咨询电话：010-56143955 010-56143855
投稿请联系 [email protected]
地址：北京市海淀区苏州街名商大厦1101环球物理
参加物理集训营拨打咨询电话，短期高效提高物理！欢迎拨打咨询电话：13581994719
