
蝶
赤橙黄绿千百色,东西南北伴芳眠。
梦里庄周游云雾,却见夏蝶迎秋山。
才子佳人泪执手,花丛翩翩续前缘。
作茧自缚何足惧,待得春风满人间。
——by 小编
正如开头诗所言,自古以来,蝴蝶就伴随着许许多多如梦似幻的意向,出现在各种文献中,其中最出名的莫过于庄周梦蝶,梁祝化蝶这类典故了。蝴蝶是文人们睡梦里的常客,是连接梦境和现实之间的纽带;抑或是才子佳人的寄托,在现实过于残酷的时候在来世中淡化悲剧色彩。古人擅长遐想,今人则擅长励志——毛虫破茧成蝶的蜕变过程,则为各种现代散文小说所津津乐道,并俨然
成为青春期成长的代名词
。或许很多读者在中学作文中都使用过“破茧成蝶”的素材。
不过蝴蝶可不仅仅只出现在文学作品中,也不只是中国人的专利。著名的“蝴蝶效应”最早则是由美国数学家兼气象学家爱德华∙罗伦兹
(Edward Lorenz,区别于物理学家洛伦兹Lorentz)
于1963年提出[1]。这一概念一经提出便引起轩然大波:在学术界,洛伦兹因他的这篇论文被誉为“混沌理论之父”[2];在商业圈,蝴蝶效应经常被企业家们当作“细节决定成败”的理论信条;在娱乐圈,《蝴蝶效应》也多次作为科幻电影出现在荧幕上,留给观众热烈的讨论。

爱德华∙罗伦兹
以讹传讹的蝴蝶效应
那么蝴蝶效应到底是什么呢?或许多数读者都听说过这么一个比喻:“一只南美洲亚马逊河流域热带雨林中的蝴蝶,偶尔扇动几下翅膀,可以在两周以后引起美国得克萨斯州的一场龙卷风”。这个比喻的目的是想告诉我们,任何一个看似微不足道的变化都可能引发巨大的连锁反应。
事实上上面这个广为流传的比喻有诸多不合理之处。当小编第一次看到这个解释的时候一直心生疑惑,既然蝴蝶在美国的地位并没有在中国那么高,那么为什么一定要用“蝴蝶效应”来描述这个现象,为什么不是蚂蚁效应、蜻蜓效应呢?既然蝴蝶拍拍翅膀就能引发龙卷风,那小编趴地上做几个俯卧撑,只怕会引起美洲大陆和欧亚大陆碰撞了。
很显然,“蝴蝶效应”的原本解释具有误导性
既然我们所经常听说的解释不那么正确,但“蝴蝶效应”这个词又的确是由罗伦兹本人本人创造的。那么罗伦兹到底是怎么想的呢?我们来看看他的这篇论文到底说了什么[1]。
奇异吸引子(Strange Attractor)——非线性系统的一大杰作
尽管论文[1]研究的是天气系统的变化,并且发表在了大气科学年刊上,但这篇文章的灵魂其实是一个三元一阶常微分方程组:
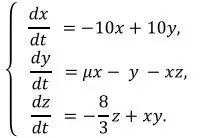
有微分方程基础的读者都知道,这看起来是一个很简单的方程组,怎么会有这么大的名气呢?我们先暂时不关心x,y,z具体表示什么,先看看当𝜇=28时,上述方程数值模拟的结果:
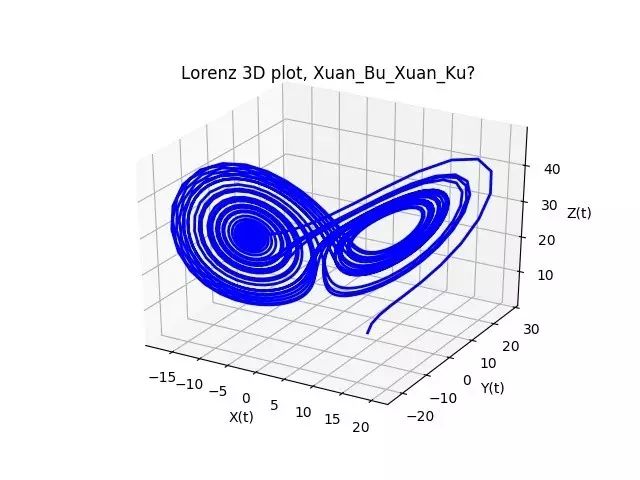
x,y,z的三维图,是不是有几分像蝴蝶?
所以,这才是罗伦兹命名“蝴蝶效应”的真实原因。
不过这么一幅蝴蝶般绚烂的模拟图,似乎应该是艺术家们的宠儿,这又是如何同神秘莫测的混沌理论拉帮结伙的呢?事实上只要我们把初始条件稍微修改一点点,我们立马就得到了完全不同的模拟结果
(代码可参见[10],小编用了Java中的StdDraw包)
:

横纵轴分别是x和z,很像两只蝴蝶的相伴相随
“差之毫厘,谬以千里”,古人的智慧在数学方程式中得到验证,这大概也算是不同思想之间穿越时空的不谋而合了。
分歧理论——
混沌理论的命根子
小编在《世界到底是不是确定的?》(
传送门
)中提到过,所谓“混沌”就是《周易》中的“无极”状态,是混乱和不可预知的代名词。那么如此简单的方程组,为什么就具有不可预知的特性呢?答案:方程右边的非线性特性。

如果我们令v表示三维向量,v=(x,y,z),那么我们可以把这个方程分解成线形和非线性两个部分:

一个线性微分方程组
(又称为线性系统)
的解是否稳定,也就是能否得到收敛解,完全依赖于矩阵A的特征值大小。若A的特征值的实部
(特征值有可能是复数)
全都小于零,那么这个方程一定是稳定的
(至少局部稳定)
。例如一维情况,v' (t)= -v(t)的解是v(t) = C*exp(-t),当t无限大时,v收敛到0这一点,所以是稳定的;一颗老鼠屎打坏一锅粥,只要
有一个
特征值的实部大于零,那么很不幸,这个方程的解就只好发散了。
但若A的某个特征值实部为零,情况就复杂了。数学上甚至有一个专门的分支来研究这种情况,这个分支就是所谓的
分歧理论
(Bifurcation Theory)
。分歧理论将凝聚态物理、多体问题、自发性对称缺失、微分方程、微分流形、微分拓扑、群表示论、气候变化等众多前沿领域贯穿成一个整体,是现代数学的一大研究核心。文献[4]、[5]、[6]和[7]分别通过
方程
(主要基于朗道的平均场和序参数理论)
、
几何
(用流形手段研究哈密顿动力系统)
、
代数
(用群表示论研究解的对称性)
和
拓扑
(用拓扑度理论研究解的宏观结构)
四种不同观点看待分歧理论,充分体现了这一领域的多样性,供不同背景和有兴趣的读者参考。
通过简单计算可以发现,若在罗伦兹的方程中取𝜇=1,那么A的有一个特征值λ1正好等于零
(因此实部也是零)
,其他两个特征值λ2、λ3都小于零。更为奇妙的是,若
𝜇在
𝜇=1
附近变化,
λ1的符号也会随着变化。就好比婚后家庭的财产稳定性多半掌握在老婆手上,
𝜇在1附近的波动从而决定了整个方程的稳定性
,所以
𝜇=1称之为方程的
分歧点
(Bifurcation Point)
。
从这个角度看来,分歧点无非就是
使方程稳定性发生变化的模型参数值
,而分歧理论的主要目的,就是研究分歧点的性质。尽管文献[4]-[7]研究分歧理论的手段各不相同,但上述宗旨始终不变。
经过简单的计算我们可以发现,当𝜇<1时, v=(0,0,0)是唯一的稳定解;当
𝜇>1,
v=(0,0,0)尽管也是解,但不再稳定,与此同时出现了两个新的稳定解。不稳定解的个数一分为二,这就是分歧,更准确地讲叫做
次临界分歧
(Subcritical Bifurcation)
。用势能的观点能更好理解这一点
(把A(
𝜇
)想像成一个和
𝜇有关的势能函数
)
:
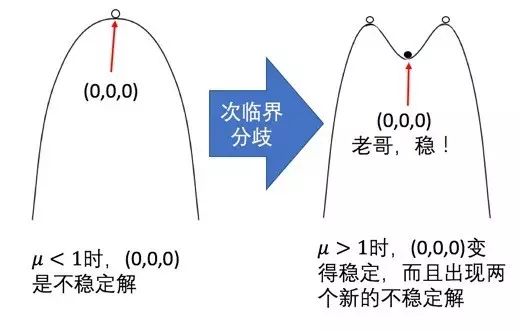
有了次临界,自然也有
超临界分歧
。读者们也许可以猜到,超临界和次临界是一对相反的分歧变换:
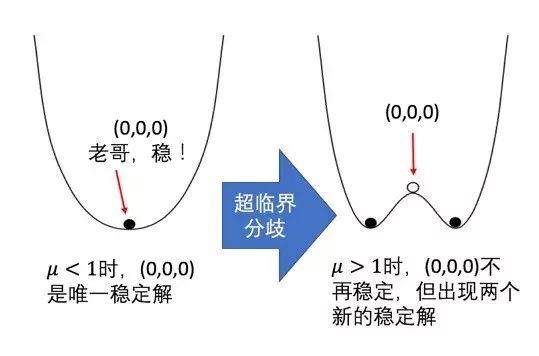
在数学家眼里,分歧图像则是这样的
(以超临界分歧为例)
:

三叉戟分歧
这看起来很像三叉戟,所以上面两种分歧又称为
三叉戟分歧
(Pitchfork Bifurcation)
。以此类推,我们甚至还可以定义四
叉戟、五
叉戟分歧等。不过数学家们只喜欢考虑最基本的情形,命名的任务就交给语言专家去完成吧。
混沌是怎么产生的?
事实上三叉戟分歧只是分歧点的一种类型。科学家们最感兴趣的分歧点类型,叫做
霍普夫分歧
(Hopf Bifurcation)
。
读者们先不要被这个高大上的外国名字吓到了。作为分歧点的一种,霍普夫分歧归根结底还是由于方程参数变化引起的矩阵特征值变化,只不过从图像上看来,方程的解从一点变成了一个
周期解
(又叫做极限环)
[8]:
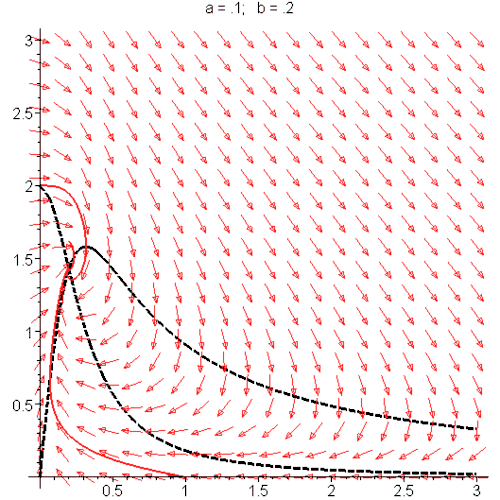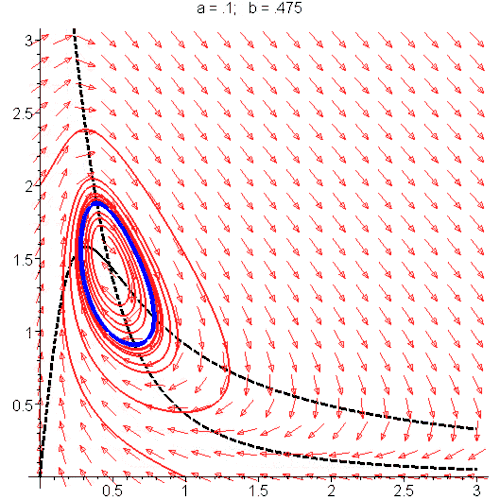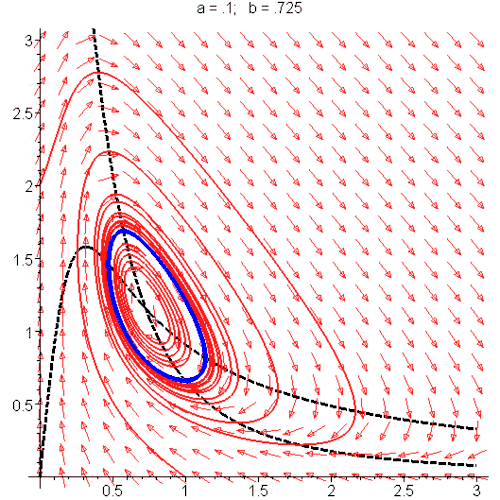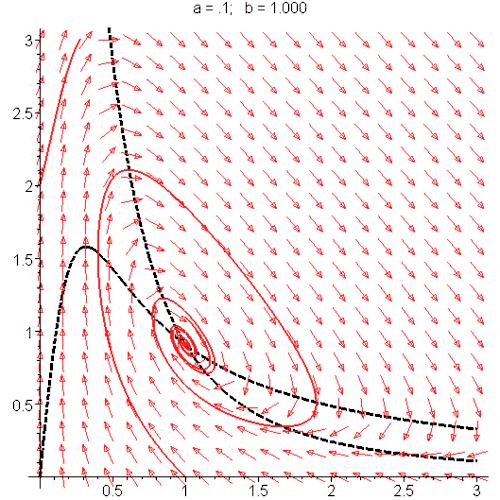
随着参数变化,蓝色的极限环(周期解)出现又消失,潮起又潮落
和线性方程不同,
由于一般情况下非线性方程会有不同的解
(例如一元二次方程一般有两个解)
,每一个解都可能发生分歧现象。而大部分混沌的出现都是
由于非线性方程不同解在同一参数下发生霍普夫分歧
。这便是非线性系统复杂性的一个根本原因。
例如对于罗伦兹方程而言,当
𝜇从
𝜇=
1
(次临界分歧点)
增加到
𝜇=470/19的过程中,方程的几个解会同时多次发生霍普夫分歧产生极限环,随后极限环又消失。这个三维系统的周期性反反复复,于是就产生了第二部分中的奇特景象。关于具体的理论分析,文献[3]给出了非常精彩而详细的证明
(文献[3]是小编见过的最全面的一本偏微分方程专著,前面五章都需要极强的数学基础。若只想了解罗伦兹奇异吸引子的产生原因,可以直接跳至第六章)
。文献[9]是相对早期的推导,但不及文献[3]深刻。
值得注意的是,罗伦兹的方程是从流体力学中的纳维・斯托克斯方程
(Navier Stokes Equation)
的一个变种简化出来的。原方程如下所示:

看似复杂的方程实际上就是动量、能量和质量三个守恒定律
罗伦兹方程中的x,y,z分量,其实是把上面方程化成极坐标以后,根据大气环流周期性而确定的一种振幅[3]。如此简单的罗伦兹方程已经展现出了内在的复杂性,而原来
纳维・斯托克斯方程的复杂性则更是可见一斑。这就是为什么
纳维・斯托克斯方程在工科和数学领域都如此受关注的原因。
化混沌为清流
本文介绍的罗伦兹方程只是混沌理论的一个简单例子。很多很多其他例子,例如chua电路[11]、SEIR传染病模型
(例如麻疹)
[12]和破坏熵增原理的Belousov–Zhabotinskii化学反应[13]等等,在数学模型上和罗伦兹系统非常相似,都是三元非线性方程,这些内容会在以后继续介绍。另外,如果方程只是二元的,那么著名的
庞加莱-本迪克松定理
(Poincare-Bendixson Theorem)
保证此时不会有混沌现象的发生。这就是为什么三体系统会产生混沌,但二元系统则不会。
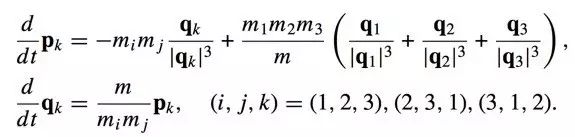
通过哈密顿动力学得到的三体问题的方程描述
混沌理论是研究复杂性的学科,这名字看起来似乎就容易让人敬而远之。但通过本文的介绍,希望读者们都对混沌理论的核心思想有了大概的认识。一言以蔽之,混沌理论的基础是分歧理论,而分歧理论的研究中心是
方程解的稳定性是如何发生改变的
,其数学本质是
方程
参数变化诱使矩阵特征值的符号发生变化
。
科学发展到今天,一方面新的分支在不断出现,另一方面不同分支之间交流之间相互交融,这一点像极了罗伦兹混沌的产生过程——霍普夫分歧不断出现与交互赋予了它蝴蝶般的神秘色彩。不过万物皆有根,就好比混沌理论的“根”栖息于矩阵特征值中一样,如果我们能找到不同分支的共同“根”,这将非常有助于对现代科学的全面理解。
作为结尾,送大家诗一首:
混沌寻根
雨蝶挥翅踏春去,三月扶摇围城来。















