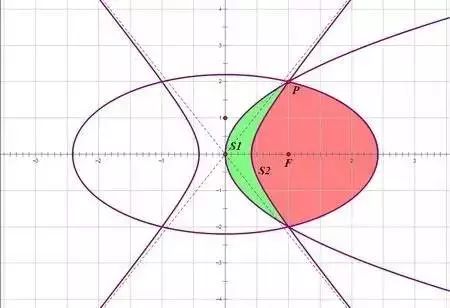
那就纳闷了,这样的一些曲线为什么叫圆锥…曲线?
难道与圆锥有关?还真是。
这要从2000多年前的古希腊数学家阿波罗尼奥斯(Apollonius of Perga,约公元前262~190年)谈起。

阿波罗尼奥斯
阿波罗尼奥斯常和欧几里得、阿基米德合称为亚历山大时期的“数学三杰”。
阿波罗尼奥斯年青时到亚历山大跟随欧几里得的后继者学习。阿波罗尼奥斯总结了前人(柏拉图学派的梅内赫莫斯为解决倍立方体问题而发现了圆锥曲线)的工作,尤其是欧几里得的工作,写了一部经典巨著《圆锥曲线论》,一共8大卷,共487个命题,前4卷的希腊文本和其次 3卷的阿拉伯文本保存了下来,最后一卷遗失。
阿波罗尼奥斯在其著作中使用纯几何方法将圆锥曲线的性质网罗殆尽,几乎不给后人留有任何研究的余地,堪称希腊几何的最高水平。(与欧几里得的《几何原本》同被誉为古代希腊几何的登峰造极之作。)

我们很难想象,在没有现代代数符号的情况下,他是如何发现并证明百条优美而深奥的定理的。不愧是“数学三杰”之一!
阿波罗尼奥斯采用平面切割圆锥的方法来研究这几种曲线。
用垂直于锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面倾斜到“和且仅和”圆锥的一条母线平行时,得到抛物线;用平行于圆锥的轴的平面截取,可得到双曲线的一支(把圆锥面换成相应的二次锥面时,则可得到双曲线。
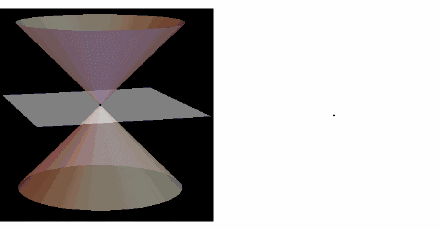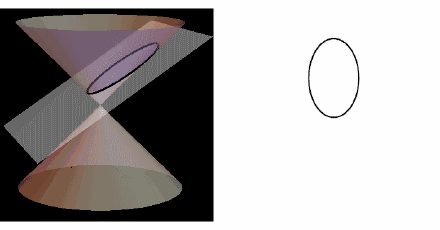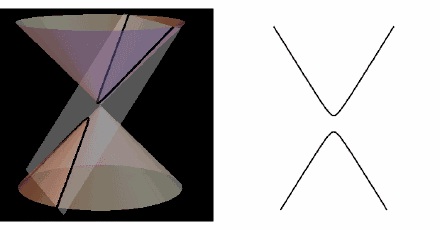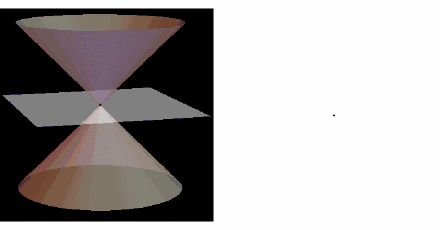
他曾把椭圆叫“亏曲线”,把双曲线叫做“超曲线”,把抛物线叫做“齐曲线”。
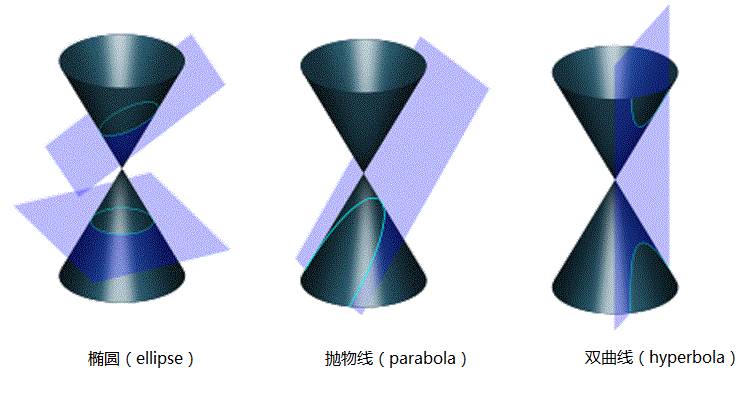

直到1800年之后的17世纪天才人物B.帕斯卡(Pascal,1623-1662) 的出现,圆锥曲线的研究才开始有了突破。

天才少年帕斯卡17岁写成的《圆锥曲线论》8页论文。在文中得出了一些特殊的结论。可谓别开生面。文中包含了三条定义,三个引理和一些定理。其中一个定理被认为是射影几何上最重要的定理。
“圆锥曲线的内接六边形,延长相对的边得到三个交点,这三点必共线”。该定理命名为帕斯卡定理,定理中的六边形叫做“神秘六边形”。
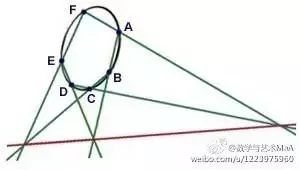
而当法国另外两位数学家R.笛卡儿(Descartes)和费马创立了解析几何,人们对圆锥曲线的认识进入了一个新阶段,对圆锥曲线的研究方法既不同于阿波罗尼奥斯的几何法,又不同于投射和截影法,而是朝着解析法的方向发展,即通过建立坐标系,得到圆锥曲线的方程,进而利用方程来研究圆锥曲线,以期摆脱几何直观而达到抽象化的目标,也可求得对圆锥曲线研究高度的概括和统一。 这也是我们现高中教材的主要编排思路。

R.笛卡儿 费马
值得一提的是,由比利时数学家G.F.Dandelin 1822年得出的冰淇淋定理证明了圆锥曲线几何定义与焦点-准线定义的等价性。
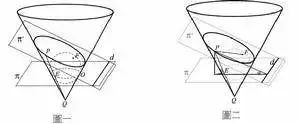
真正将圆锥曲线的研究拉回生活,而不再是象牙塔里的抽象事物的,则是16世纪所发生的两件事,促使了人们对圆锥曲线作进一步研究。
一是德国天文学家开普勒(Kepler,1571~1630)继承了哥白尼的日心说,揭示出行星按椭圆轨道环绕太阳运行的事实。
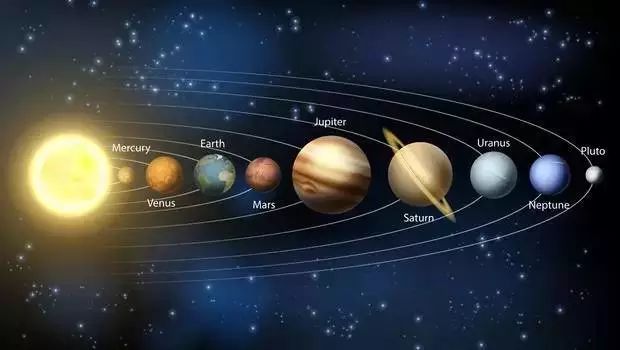
我们生活的地球每时每刻都在环绕太阳的椭圆轨迹上运行,太阳系其他行星也如此,太阳则位于椭圆的一个焦点上。如果这些行星运行速度增大到某种程度,它们就会沿抛物线或双曲线运行。人类发射人造地球卫星或人造行星就要遵照这个原理。
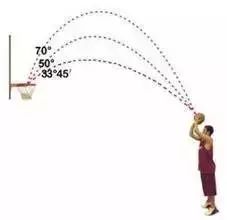
二是意大利物理学家伽利略(Galileo,1564~1642)得出物体斜抛运动的轨道是抛物线。

我们发现圆锥曲线不仅是依附在圆锥面上的静态曲线,而且是自然界物体运动的普遍形式。因而,圆锥曲线在这种意义上讲,它构成了我们宇宙的基本形式。
这个事情的发生本身就很是意思。
没有人知道纯粹数学何时能得到意外应用。正如William Whewell(首创"科学家"一词)所说:"假如希腊人不应用圆锥曲线,开普勒就不可能取代托勒密。"有趣的是,希腊人运用圆锥曲线只是为了他们对知识的渴望,而在1800年后,它们竟发挥作用如此重要的实际作用。
手电筒射出来的光束,圆形灯罩里的台灯照出来的光束,天花板上的筒灯里照出来的光束,可以视为圆锥形。
光束照到墙上,就好比用平面(墙)去截圆锥,光照到的亮处与没有照到的地方的暗处的分界线就是平面与圆锥的交线,就是圆锥曲线。
调整手电筒照射的方向,可以得到圆、椭圆、抛物线、双曲线。台灯和筒灯照出来的圆锥形光束的轴基本上与墙平行,得到的交线是双曲线的一支。

【定义作图法】我们常用的最简单实用的方法,就是依据“平面内到定点F1、F2的距离之和等于常数(大于|F1F2|)的动点P的轨迹”。(这是 1579年蒙蒂(Guidobaldo delMonte,1545~1607)给出的椭圆定义)
而作图法据说出自建造圣索菲亚大教堂的数学家安提莫斯,称为“园艺师作图法”。
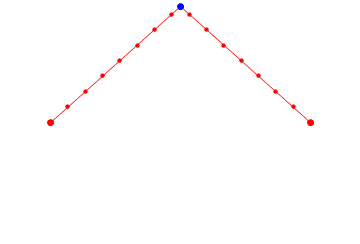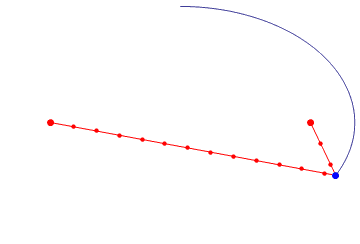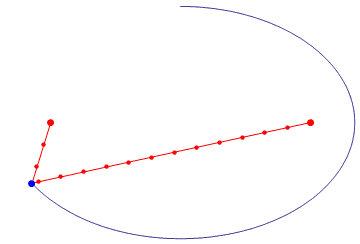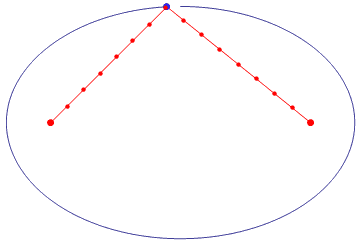
【原理直观化】简洁明了!由比例关系得到椭圆,是不是好萌!
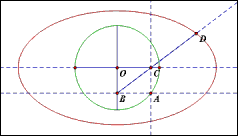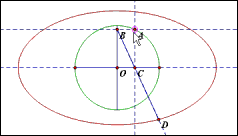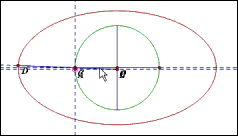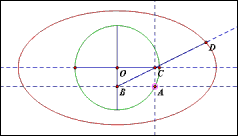
当然,市面上流行的椭圆规也别具一格。

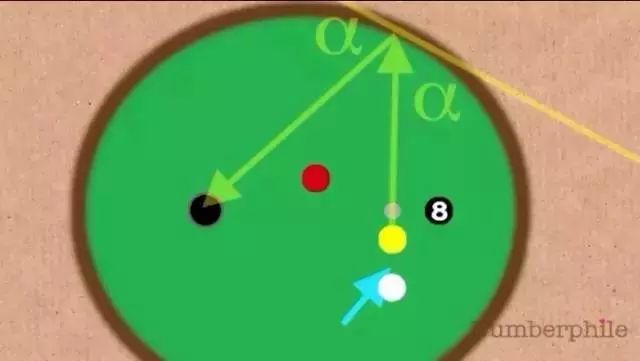
从椭圆的一个焦点发出的光线或者声波在经过椭圆周上反射之后,反射都经过椭圆的另一个焦点。(最早提出焦点概念的正是开普勒)

【椭圆桌面●循环游戏】这个有意思!


由抛物线绕其轴旋转,可得到一个叫做旋转物面的曲面。它也有一条轴,即抛物线的轴。在这个轴上有一个具有奇妙性质的焦点,任何一条过焦点的直线由抛物面反射出来以后,都成为平行于轴的直线。这就是我们为什么要把探照灯反光镜做成旋转抛物面的道理。

据说,“数学之神”阿基米德就曾利用铜镜烧了敌人船只。这大概是夸张的说法。不过当时阿基米德确实已经发现抛物面反射镜能够聚焦的性质。


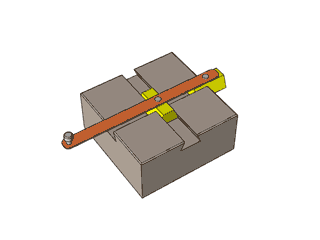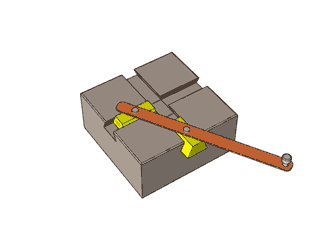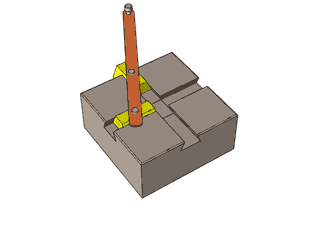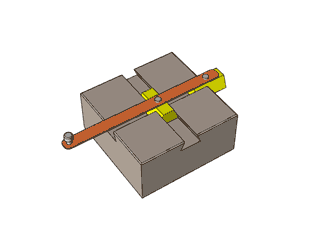
一根直杆怎么能从弯曲的洞中穿过?
原来这弯曲的洞是双曲线的一支。
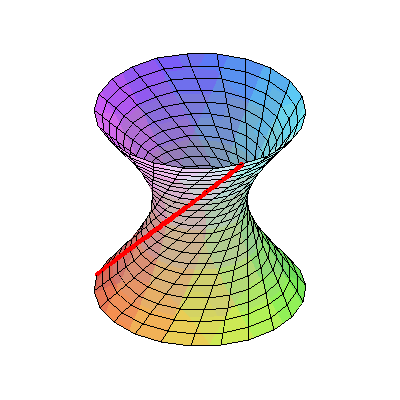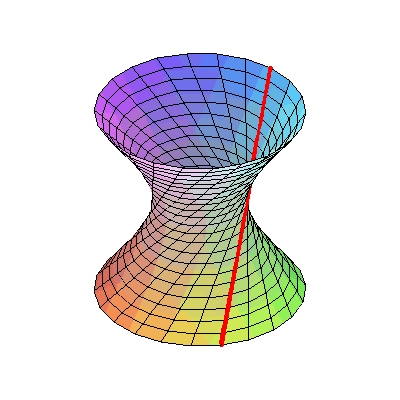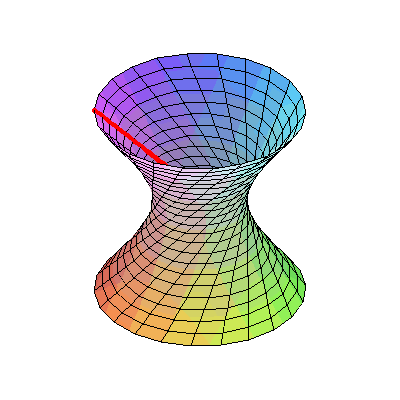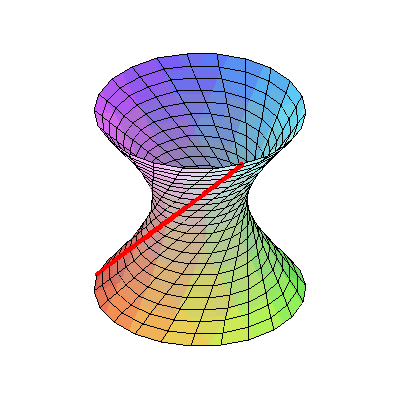
把这个曲线绕旋转轴旋转一周,形成一个曲面,叫做单叶双曲面。
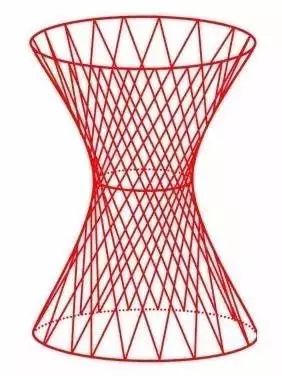
有意思的是,这条双曲线是一种直纹曲面。它是可以由一条条直线所织成的。比如圆柱面、圆锥面都是直纹曲面。
单叶双曲面也是如此,只不过它上面的直线看起来不是那么显而易见,这些直线是倾斜的。这就是上面那根杆是斜着的才能穿过的原因。
又如下面这个时钟:曲中蕴直线,直走成曲面。好创意!

单叶双曲面还有一个神奇的地方:通过它上面的每一个点,都有两条直线在曲面上。
又如双曲抛物面也是一种直纹面。
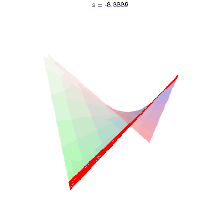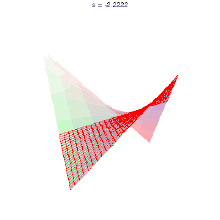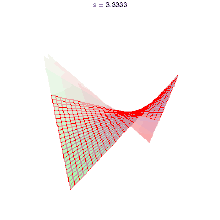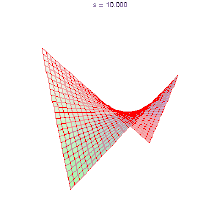


单叶双曲面作为一种直纹面,在现代建筑设计中也已属常见。日本神户港塔、各种冷却塔、广州电视塔、圣路易斯科学中心天文馆、巴西利亚大教堂、在德国黑默尔本的木制瞭望塔、还有上海世博沙特馆等。这样的体形既轻巧又坚固。



王渊超于1995年读高中时创作了这首歌曲。据说,创作的灵感正是来源于一堂解析几何课,当时老师正在论证讲解“双曲线与渐近线只能无限接近不能达到”,而正是这点给王渊超带来了创作动机,并在笔记本上把歌词一挥而就。
music
如果我是双曲线,恩~你就是那渐近线
如果我是反比例函数,你就是那坐标轴
虽然我们有缘,能够生在同一个平面
然而我们又无缘,恩~慢慢长路无交点
为何看不见,等式成立要条件
难到正如书上说的,无限接近不能达到
如果我是双曲线,恩~你就是那渐近线
如果我是反比例函数,你就是那坐标轴
虽然我们有缘,能够生在同一个平面
然而我们又无缘,恩~慢慢长路无交点
为何看不见,等式成立要条件
难到正如书上说的,无限接近不能达到
为何看不见,明月也有阴晴圆缺
此事古难全,但愿千里共婵娟
此事古难,但愿千里共婵娟
其实,这哪里是什么悲伤的双曲线?
渐近线,越走越近,又给了彼此空间!
·END·
* 本文获授权转载自微信公众号:数学与艺术MaA (ID: MathAndArt)
以数学学习为主题,以传播数学文化为己任,以激发学习者学习数学的兴趣为目标,分享有用的数学知识、有趣的数学故事、传奇的数学人物等,为你展现一个有趣、好玩、丰富多彩的数学世界。















