背景准备
前面我们用了很多的笔墨来介绍如何建立线性回归模型和非线性回归模型:
今天给大家介绍利用分段回归模型拟合的办法来处理一些特殊的变量关系。某些变量之间的关系非常有趣,不是恒久的线性或非线性关系,可能其中一段表现为线性,而另一段表现为非线性。例如,我们举一个每个人都有切身体会的例子,人的身高和年龄的关系,在3岁到10岁期间,它们基本是线性相关,而高中以后,身高基本定型,不再随年龄的增加而增长。对于这样的变量关系,在3到10岁期间,我们可以用一个线性方程来拟合年龄和身高的关系,而高中以后则需要换另一个方程,可以是线性的,也可以是非线性的,需要根据数据情况来选择。这就是分段回归模型的分析思路。
分段回归模型
对于相关关系在自变量取值区间上不是恒定不变的情况,我们可以只分析某一部分明确相关关系的数据,这样可以保证结果的简洁和稳定;当需要考虑整个自变量取值区间时,就必须要包含整个取值区间的数值,此时,如果整个区间可以用几个分段回归模型表达,那么就可以进行分段拟合。通常的做法是对每个部分进行单独拟合,但是这样做参数较多,且样本被人为分开,当样本量较小时会导致分析结果的准确性很差。
SPSS的非线性回归模块完美的解决了这个问题,可直接对分段函数进行直接拟合,以充分利用信息,提高模型的预测精度。由于原理简单,我们下面用一个具体的案例来介绍如何利用SPSS进行分段回归模型拟合。
生活案例
近几年,每年夏天关于全国用电紧张的新闻报道都会准时出现。造成用电紧张的原因很多,一方面是全球变暖这个总体大趋势的影响,人们需要用各种电器消暑降温;另一方面是科技的进步,各种空调冰箱等电器走进千家万户,用电量自然水涨船高。电量吃紧最紧张的就是国家电网,某地电业局打算通过过往数据的分析,建立模型来准确预测各种温度状况下的用电负荷,以期提高电网运行和能源调配的效率。下面有一份数据,记录了该地去年5 月到8月的日平均气温,以及当天的居民用电总量,希望建立居民用电量与日平均气温间的预报方程。
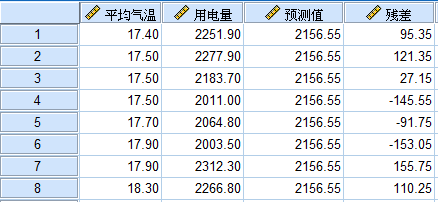
(例题数据文件已经上传到QQ群,群号请见文章底部温馨提示)
分析思路
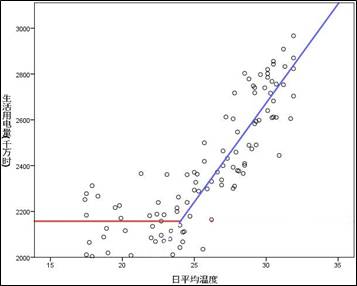
为了能够对气温和用电量之间的关系有基本了解,两变量的散点图是最直观的工具。首先绘制日平均气温和居民生活用电量间的散点图,然后根据散点图展示的变量关系,来选择合适的回归模型。散点图的作图方法前面介绍过(【图形】-【图标构建器】),这里就不在赘述,直接给出下面的结果。
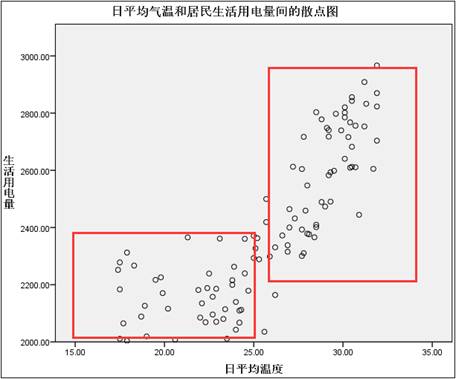
由上图可知,日平均气温对用电量的影响分成两个阶段:24摄氏度以下时,用电量并不会随着气温的改变而显著增加;24摄氏度以上时,用电量随着平均气温的上升呈现明显的上升趋势。因此,该数据的模型可以这样写:

分析步骤
选择菜单【分析】-【回归】-【非线性回归】;在跳出的对话框中作如下操作。将生活用电量选为因变量,在模型表达式框内输入(平均气温 < 24)*b1+(平均气温 >= 24)*(a2*平均气温+b2);点击参数,设置表达式中的三个参数,由于是比较线性模型,迭代初始值都设置为1。点击继续,然后点击确定,输出结果。
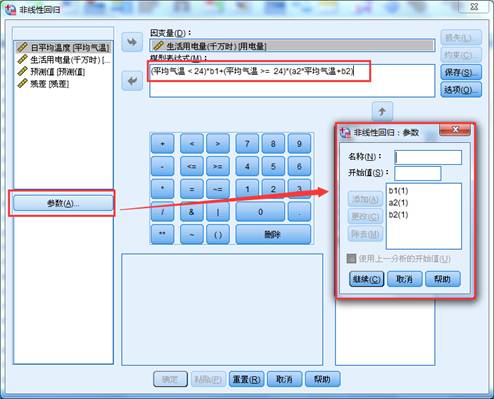
结果解释
1、模型的方差分析结果;
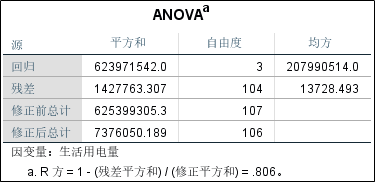
由结果可知,分段回归模型总的决定系数达到0. 806,说明模型的拟合效果不错。
2、模型参数值表格;
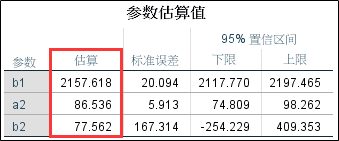
根据模型参数值表格,我们可以写出两个回归方程:

为了验证根据前面我们根据散点图选定的24摄氏度趋势分界点是否为数据的合理趋势分界点,将24摄氏度代入回归方程2,可算得用电量的估计值为2157. 52,因此以24摄氏度作为分段点是比较合理的。
3、残差图分析;
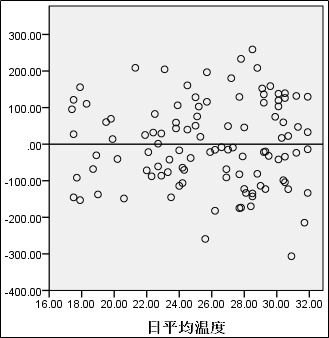
上图是自变量与残差的散点图,可见在24摄氏度前后,残差的分布都是随机的,且前后没有明显变化,离散程度基本相同,因此对数据进行分段回归模型拟合是合理的。
所有例题的数据文件都会上传到QQ群中,需要对照练习的朋友可以前往下载,QQ群号见下方温馨提示。
温馨提示:















