
在1997年的四国赛上,巴西队的
罗伯特·卡洛斯
任意球中创造了一个惊人的“不可能的进球”。
这也是足球史上最经典的“
香蕉球
”之一。

摄像大哥都被晃了一下
不得不说“香蕉球”这个名字也是非常形象了,它在空中运动的轨迹真的和香蕉的弧线很像。
当然,这种球也必须要球员用特殊的脚法才能踢出来的。

想踢出香蕉球,就不能踢得很直
不光是足球,在各种球类比赛中,这种
弧线球
往往都能起到出奇制胜的效果。
毕竟在每个人的直觉中,球的运动轨迹就应该是直的。
我们也都在物理课上学过:“
物体都有维持静止和匀速直线运动的趋势。
”

牛顿第一定律
假的
那么,到底是什么神秘力量,把这些本应遵循“牛顿第一定律”的球都给掰弯了呢?
巧的是,最早发现弧线球的现象并对其做出解释的人,就是牛顿本人。
1672年,牛顿在观看剑桥网球比赛的时候,注意到旋转能够迫使网球下降得比预期的要快。
但要是让球以相反的方向旋转,反而会让球产生类似于漂浮的效果。
弧线球的秘密,在于旋转。
以一个顺时针旋转的球为例,当这个球在空气中运动时。在它前进方向的右侧,旋转方向和气流方向相同,这部分气流就被温和地“掰弯了”。

我们可以画出这样的示意图来↓↓↓
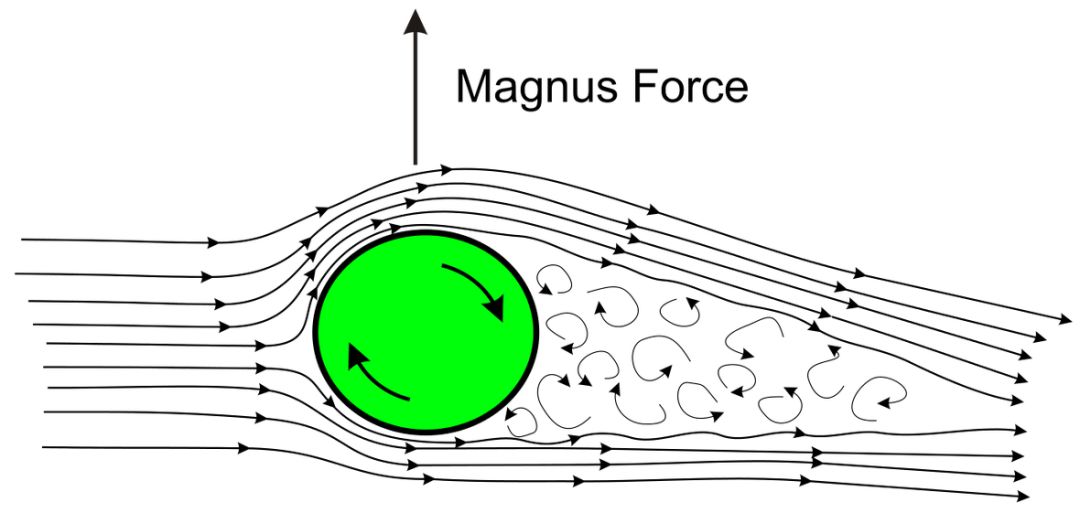
有了这个气流图,我们就可以一探弧线球背后的原理了。
最直观的解释来自于牛顿的第三定律。
(相互作用的两个物体之间的作用力和反作用力总是大小相等,方向相反,作用在同一条直线上)
旋转的球“掰弯”了气流,这相当于球给了气流一个力,所以气流也会给球一个反作用力。
就是这个“反作用力”反来过掰弯了球的运动轨迹。

牛顿第三定律
假的
另一种解释
常被用来回答“飞机为什么会在天上飞?”这一问题。
说起飞机,大家有没有发觉弧线球的气流示意图和飞机机翼的长得很像?
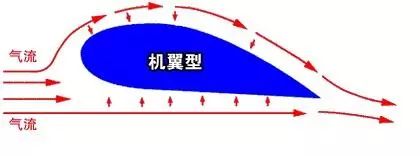
机翼周围气流示意图
依据伯努利原理,我们得知
“
流速大的地方压强小
”
。
放到弧线球上,在球的一侧空气流速较快,压强较小;而在另一侧空气流速慢,压强较大。
正是因为这个压强差的存在,球被压得不断偏离原本的运动方向,从而划出了一条弧线。
顺带一提,其实人们至今都无法对“飞机为什么会在天上飞?”这一问题给出一个确切的答案,伯努利原理只是这个问题的“可能解释”之一。
在牛顿发现这种“掰弯效应”100多年后,一位叫
古斯塔夫·马格纳斯
的实验科学家做了一系列实验,试图弄清楚为什么旋转炮弹有时会以不可预知的方式跑偏。
马格纳斯最终总结描述了这一效应:
在气流中旋转的球体或圆柱体会受到与气流方向垂直的力,且这个力指向气流方向与旋转方向相同的一侧。
说起来~虽然是牛顿最早发现的这一效应,但以牛顿命名的东西实在太多了,也不差这一个。

维基上“以牛顿命名的事物列表”中收纳的词条有55个
于是后来的人们就把“冠名权”给了马格努斯,将这一效应称为“
马格纳斯效应
”。
这个“马格纳斯效应”除了在体育运动中大显身手,在别的领域也有一些应用。
就像我们刚才说的,弧线球和飞机在原理上有共通之处,那么我们显然可以利用这一原理来造飞机。

AA-2004旋翼飞机 ,曾成功飞越长岛海峡(最宽的地方也才34公里)
不过,可以飞不等于适合飞,对于这种叫做弗莱特纳飞机的飞行器来说,光是维持不掉下来就已经竭尽全力了,要是还想让它载个人拉个货那可就太难为它了。
所以现在人们也没什么机会能看到它,也就偶尔有科技爱好者做一个模型出来当玩具。
相比之下,把“马格纳斯效应”应用在
航海领域
就显得靠谱一些了。






