转自知乎
作者：张觉非 阿里巴巴 友盟+
机器之心经作者授权转载
链接：https://zhuanlan.zhihu.com/p/25249694
一、卷积
我们在 2 维上说话。有两个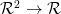
的函数 f(x,y) 和 g(x,y)。f 和 g 的卷积就是一个新的
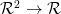的函数。通过下式得到：
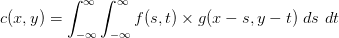
这式子的含义是：遍览从负无穷到正无穷的全部 s 和 t 值，把 g 在 (x-s,y-t) 位置上的值乘上 f 在 (s,t) 位置上的值之后「加和」（积分意义上的加和）到一起，就是 c 在 (x,y) 上的值。说白了卷积就是一种「加权求和」。以 (x,y) 为中心，把 g 距离中心 (-s,-t) 位置上的值乘上 f 在 (s,t) 的值，最后加到一起。把卷积公式写成离散形式就更清楚了：
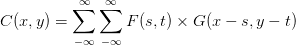
如果 G 表示一幅 100 x 100 大小的灰度图像，G(x,y) 取值 [0,255] 区间内的整数，是图像在 (x,y) 的灰度值。范围外的位置上的 G 值全取 0。令 F 在 s 和 t 取 {-1,0,1} 的时候有值，其他位置全是 0。F 可以看作是一个 3 x 3 的网格。如下图：
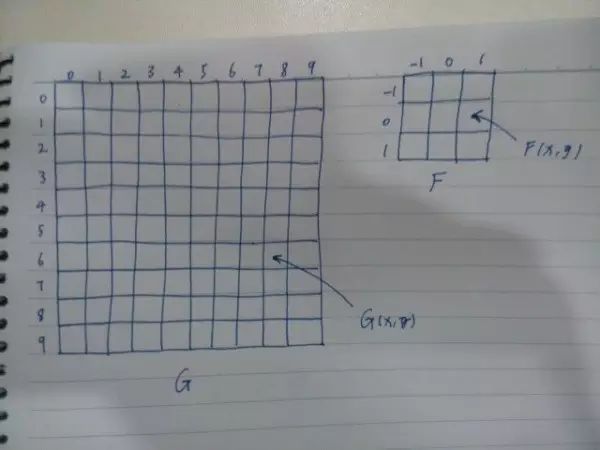
图 1
G 每个小格子里的值就是图像在 (x,y) 的灰度值。F 每个小格子里的值就是 F 在 (s,t) 的值。
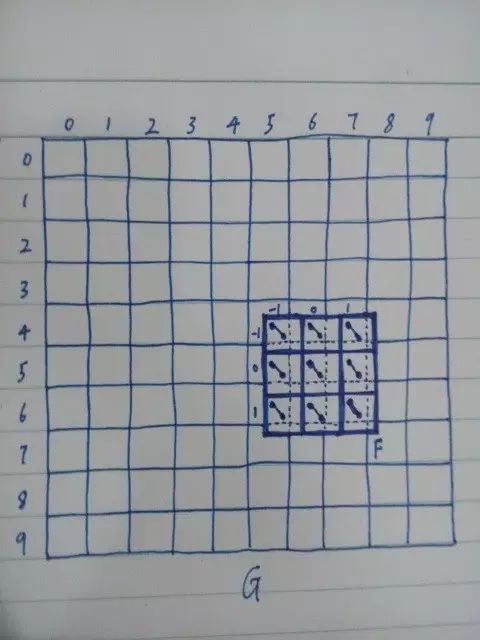
图 2
如上图所示，将 F 的中心 (0,0) 对准 G 的 (5,6)。把 F 和 G 对应的 9 个位置上各自的函数值相乘，再将 9 个乘积加在一起，就得到了卷积值 C(5,6)。对 G 的每一个位置求 C 值，就得到了一幅新的图像。其中有两个问题：
如果 F 的所有值之和不等于 1.0，则 C 值有可能不落在 [0,255] 区间内，那就不是一个合法的图像灰度值。所以如果需要让结果是一幅图像，就得将 F 归一化——令它的所有位置之和等于 1.0 ；
对于 G 边缘上的点，有可能它的周围位置超出了图像边缘。此时可以把图像边缘之外的值当做 0。或者只计算其周围都不超边缘的点的 C。这样计算出来的图像就比原图像小一些。在上例中是小了一圈，如果 F 覆盖范围更大，那么小的圈数更多。
上述操作其实就是对数字图像进行离散卷积操作，又叫滤波。F 称作卷积核或滤波器。不同的滤波器起不同的作用。想象一下，如果 F 的大小是 3 x 3，每个格子里的值都是 1/9。那么滤波就相当于对原图像每一个点计算它周围 3 x 3 范围内 9 个图像点的灰度平均值。这应该是一种模糊。看看效果：
图 3
左图是 lena 灰度原图。中图用 3 x 3 值都为 1/9 的滤波器去滤，得到一个轻微模糊的图像。模糊程度不高是因为滤波器覆盖范围小。右图选取了 9 x 9 值为 1/81 的滤波器，模糊效果就较明显了。滤波器还有许多其他用处。例如下面这个滤波器：
尝试用它来滤 lena 图。注意该滤波器没有归一化（和不是 1.0），故滤出来的值可能不在 [0,255] 之内。通过减去最小值、除以最大／最小值之差、再乘以 255 并取整，把结果值归一到 [0,255] 之内，使之成为一幅灰度图像。
图 4
该滤波器把图像的边缘检测出来了。它就是 Sobel 算子。图像模糊、边缘检测等等都是人们设计出来的、有专门用途的滤波器。如果搞一个 9 x 9 的随机滤波器，会是什么效果呢？
图 5
如上图，效果也类似于模糊。因为把一个像素点的值用它周围 9 x 9 范围的值随机加权求和，相当于「捣浆糊」。但可以看出模糊得并不润滑。
这时我们不禁要想，如果不是由人来设计一个滤波器，而是从一个随机滤波器开始，根据某种目标、用某种方法去逐渐调整它，直到它接近我们想要的样子，可行么？这就是卷积神经网络（Convolutional Neural Network, CNN）的思想了。可调整的滤波器是 CNN 的「卷积」那部分；如何调整滤波器则是 CNN 的「神经网络」那部分。
二、神经网络
人工神经网络（Neural Network, NN）作为一个计算模型，其历史甚至要早于计算机。W.S. McCulloch 和 W. Pitts 在四十年代就提出了人工神经元模型。但是单个人工神经元甚至无法计算异或。人工智能领域的巨擘马文. 明斯基认为这个计算模型是没有前途的。在那时人们已经认识到将多个人工神经元连接成网络就能克服无法计算异或的问题，但是当时没有找到多层人工神经网络的训练方法，以至于人工神经网络模型被压抑多年。直到人们找到了多层人工神经网络的训练方法，人工神经网络才迎来了辉煌。
人工神经元就是用一个数学模型简单模拟人的神经细胞。人的神经细胞有多个树突和一个伸长的轴突。一个神经元的轴突连接到其他神经元的树突，并向其传导神经脉冲。一个神经元会根据来自它的若干树突的信号决定是否从其轴突向其他神经元发出神经脉冲。
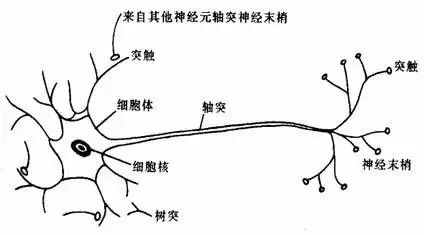
图 6
一个人工神经元就是对生物神经元的数学建模。见下图。
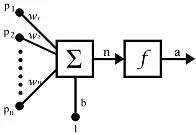
图 7
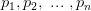是人工神经元的输入。a 是人工神经元的输出。人工神经元将输入
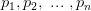加权求和后再加上偏置值 b，最后再施加一个函数 f，即：
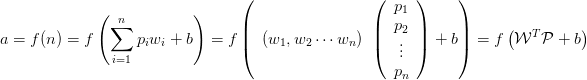
上式最后是这个式子的向量形式。P 是输入向量，W 是权值向量，b 是偏置值标量。f 称为「激活函数」。激活函数可以采用多种形式。例如 Sigmoid 函数：
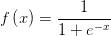
这是单个人工神经元的定义。人工神经网络就是把这样的人工神经元互联成一个网络：一个神经元的输出作为另一个神经元的输入。神经网络可以有多种多样的拓扑结构。其中最简单的就是「多层全连接前向神经网络」。它的输入连接到网络第一层的每个神经元。前一层的每个神经元的输出连接到下一层每个神经元的输入。最后一层神经元的输出就是整个神经网络的输出。
如下图，是一个三层神经网络。它接受 10 个输入，也就是一个 10 元向量。第一层和第二层各有 12 个神经元。最后一层有 6 个神经元。就是说这个神经网络输出一个 6 元向量。
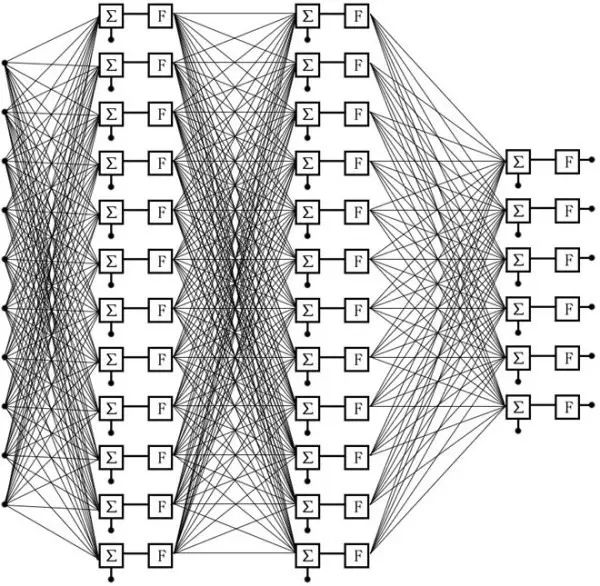
图 8
整个神经网络的计算可以用矩阵式给出。我们给出人工神经网络单层的式子。每层的神经元个数不一样，输入／输出维度也就不一样，计算式中的矩阵和向量的行列数也就不一样，但形式是一致的。假设我们考虑的这一层是第 i 层。它接受 m 个输入，拥有 n 个神经元（n 个输出），那么这一层的计算如下式所示：
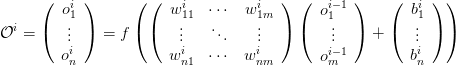
上标 i 表示第 i 层。是输出向量，n 元，因为第 i 层有 n 个神经元。第 i 层的输入，即第 i-1 层的输出，是 m 元向量。权值矩阵 W 是 n x m 矩阵：n 个神经元，每个神经元有 m 个权值。W 乘以第 i-1 层输出的 m 向量，得到一个 n 向量，加上 n 元偏置向量 b，再对结果的每一个元素施以激活函数 f，最终得到第 i 层的 n 元输出向量。
若不嫌繁琐，可以将第 i-1 层的输出也展开，最终能写出一个巨大的式子。它就是整个全连接前向神经网络的计算式。可以看出整个神经网络其实就是一个向量到向量的函数。至于它是什么函数，就取决于网络拓扑结构和每一个神经元的权值和偏置值。如果随机给出权值和偏置值，那么这个神经网络是无用的。我们想要的是有用的神经网络。它应该表现出我们想要的行为。
要达到这个目的，首先准备一个从目标函数采样的包含若干「输入－输出对儿」的集合——训练集。把训练集的输入送给神经网络，得到的输出肯定不是正确的输出。因为一开始这个神经网络的行为是随机的。
把一个训练样本输入给神经网络，计算输出与正确输出的（向量）差的模平方（自己与自己的内积）。再把全部 n 个样本的差的模平方求平均，得到 e ：
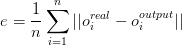
e 称为均方误差 mse。e 越小则神经网络的输出与正确输出越接近。神经网络的行为就与想要的行为越接近。
目标是使 e 变小。在这里 e 可以看做是全体权值和偏置值的一个函数。这就成为了一个无约束优化问题。如果能找到一个全局最小点，e 值在可接受的范围内，就可以认为这个神经网络训练好了。它能够很好地拟合目标函数。这里待优化的函数也可以是 mse 外的其他函数，统称 Cost Function，都可以用 e 表示。
经典的神经网络的训练算法是反向传播算法（Back Propagation, BP）。BP 算法属于优化理论中的梯度下降法（Gradient Descend）。将误差 e 作为全部权值和全部偏置值的函数。算法的目的是在自变量空间内找到 e 的全局极小点。
首先随机初始化全体权值和全体偏置值，之后在自变量空间中沿误差函数 e 在该点的梯度方向的反方向（该方向上方向导数最小，函数值下降最快）前进一个步长。步长称为学习速率（Learning Rate, LR）。如此反复迭代，最终（至少是期望）解运动到误差曲面的全局最小点。
下图是用 matlab 训练一个极简单的神经网络。它只有单输入单输出。输入层有两个神经元，输出层有一个神经元。整个网络有 4 个权值加 3 个偏置。图中展示了固定其他权值，只把第一层第一个神经元的权值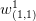
和偏置
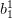做自变量时候的 e 曲面，以及随着算法迭代，解的运动轨迹。
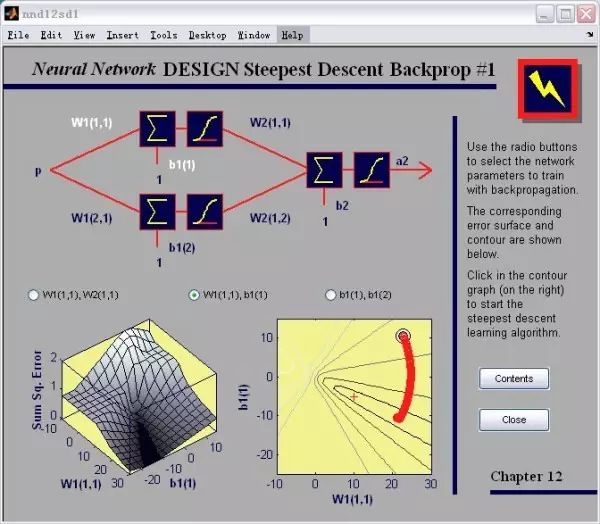
图 9
最终算法没有收敛到全局最优解（红 +）。但是解已经运动到了一个峡谷的底部。由于底部过于平缓，解「走不动」了。所得解比最优也差不到哪去。
对于一个稍复杂的神经网络，e 对权值和偏置值的函数将是一个非常复杂的函数。求梯度需要计算该函数对每一个权值和偏置值的偏导数。所幸的是，每一个权值或偏置值的偏导数公式不会因为这个权值或偏置值距离输出层越远而越复杂。计算过程中有一个中间量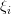
，每层的权值和偏置值的偏导数都可根据后一层的
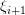以统一形式计算出来。每层再把计算过程中产生的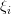传递给前一层。这就是「反向传播」名称的由来——
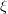沿着反向向前传。这与计算网络输出时，计算结果向后传相反。如此可逐层计算出全部权值和偏置值的偏导数，得到梯度。具体推导这里不给出了，可以参考［1］第八章和［2］第十一章。正是反向传播能够让我们训练神经网络「深处」的参数，这就是「Deep Learning」的含义。
梯度下降法有很多变体。通过调整学习速率 LR 可以提高收敛速度；通过增加冲量可以避免解陷入局部最优点。还可以每一次不计算全部样本的 e，而是随机取一部分样本，根据它们的 e 更新权值。这样可以减少计算量。梯度下降是基于误差函数的一阶性质。还有其他方法基于二阶性质进行优化，比如共轭法、牛顿法等等。优化作为一门应用数学学科，是机器学习的一个重要理论基础，在理论和实现上均有众多结论和方法。参考［1］。
三、卷积神经网络
现在把卷积滤波器和神经网络两个思想结合起来。卷积滤波器无非就是一套权值。而神经网络也可以有（除全连接外的）其它拓扑结构。可以构造如下图所示意的神经网络：
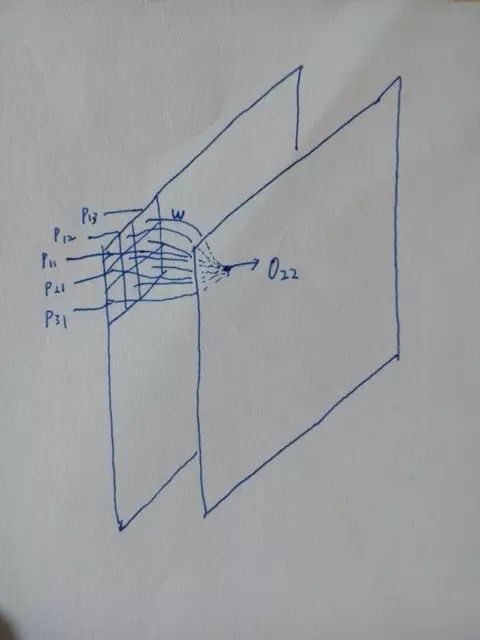
图 10
该神经网络接受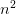
个输入，产生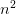个输出。图中左边的平面包含 n x n 个格子，每个格子中是一个 [0,255] 的整数值。它就是输入图像，也是这个神经网络的输入。右边的平面也是 n x n 个格子，每个格子是一个神经元。每个神经元根据二维位置关系连接到输入上它周围 3 x 3 范围内的值。每个连接有一个权值。所有神经元都如此连接（图中只画了一个，出了输入图像边缘的连接就认为连接到常数 0）。右边层的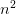个神经元的输出就是该神经网络的输出。
这个网络有两点与全连接神经网络不同。首先它不是全连接的。右层的神经元并非连接上全部输入，而是只连接了一部分。这里的一部分就是输入图像的一个局部区域。我们常听说 CNN 能够把握图像局部特征、AlphaGO 从棋局局部状态提取信息等等，就是这个意思。这样一来权值少了很多，因为连接就少了。权值其实还更少，因为每一个神经元的 9 个权值都是和其他神经元共享的。全部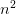个神经元都用这共同的一组 9 个权值，并且不要偏置值。那么这个神经网络其实一共只有 9 个参数需要调整。
看了第一节的同学们都看出来了，这个神经网络不就是一个卷积滤波器么？只不过卷积核的参数未定，需要我们去训练——它是一个「可训练滤波器」。这个神经网络就已经是一个拓扑结构特别简单的 CNN 了。
试着用 Sobel 算子滤出来的图片作为目标值去训练这个神经网络。给网络的输入是灰度 lena 图，正确输出是经过 Sobel 算子滤波的 lena 图，见图 4。这唯一的一对输入输出图片就构成了训练集。网络权值随机初始化，训练 2000 轮。如下图：
图 11
从左上到右下依次为：初始随机滤波器输出、每个 200 轮训练后的滤波器输出（10 幅）、最后一幅是 Sobel 算子的输出，也就是用作训练的目标图像。可以看到经过最初 200 轮后，神经网络的输出就已经和 Sobel 算子的输出看不出什么差别了。后面那些轮的输出基本一样。输入与输出的均方误差 mse 随着训练轮次的变化如下图：
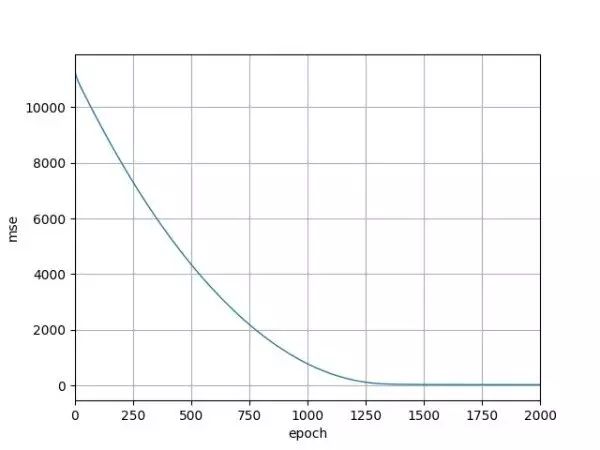
图 12
1500 轮过后，mse 基本就是 0 了。训练完成后网络的权值是：
与 Sobel 算子比较一下：
注意训练出来的滤波器负数列在右侧而不是左侧。因为用 Sobel 算子算卷积的时候也许库函数（scipy.ndimage.filters.convolve）是把滤波器「反着扣上去」的。这并不重要。关键是一正列、一负列，中间零值列。正／负列值之比近似 1:2:1。它就是近似的 Sobel 算子。我们以训练神经网络的方式把一个随机滤波器训练成了 Sobel 算子。这就是优化的魔力。AlphaGO 之神奇的核心也在于此——优化。
在 CNN 中，这样的滤波器层叫做卷积层。一个卷积层可以有多个滤波器，每一个叫做一个 channel，或者叫做一个 feature map。可以给卷积层的输出施加某个激活函数：Sigmoid 、Tanh 等等。激活函数也构成 CNN 的一层——激活层，这样的层没有可训练的参数。
还有一种层叫做 Pooling 层（采样层）。它也没有参数，起到降维的作用。将输入切分成不重叠的一些 n x n 区域。每一个区域就包含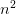个值。从这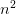个值计算出一个值。计算方法可以是求平均、取最大 max 等等。假设 n=2，那么 4 个输入变成一个输出。输出图像就是输入图像的 1/4 大小。若把 2 维的层展平成一维向量，后面可再连接一个全连接前向神经网络。
通过把这些组件进行组合就得到了一个 CNN。它直接以原始图像为输入，以最终的回归或分类问题的结论为输出，内部兼有滤波图像处理和函数拟合，所有参数放在一起训练。这就是卷积神经网络。
四、举个栗子
手写数字识别。数据集中一共有 42000 个 28 x 28 的手写数字灰度图片。十个数字（0～9）的样本数量大致相等。下图展示其中一部分（前 100 个）：
图 13
将样本集合的 75% 用作训练，剩下的 25% 用作测试。构造一个结构如下图的 CNN ：
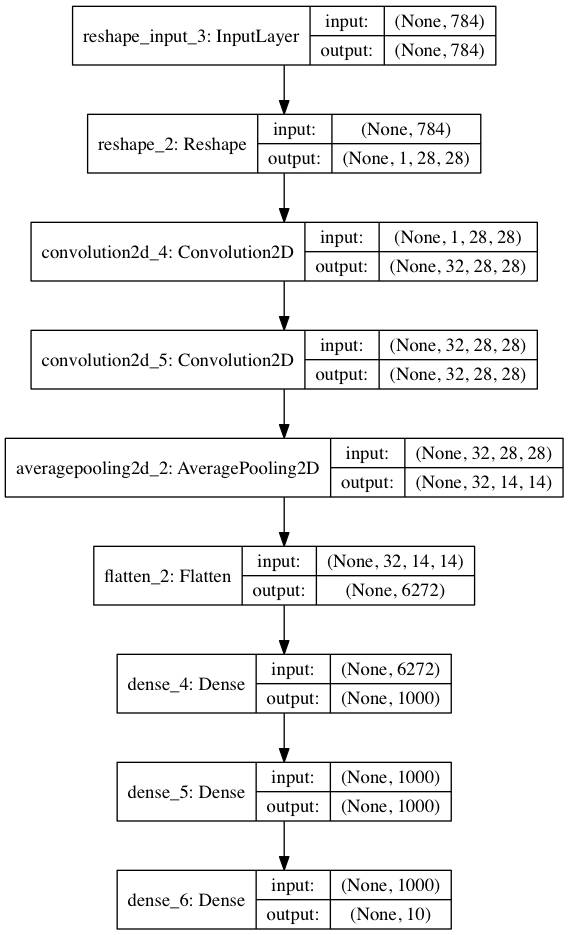
图 14
该 CNN 共有 8 层（不包括输入层）。它接受 784 元向量作为输入，就是一幅 28 x 28 的灰度图片。这里没有将图片变形成 28 x 28 再输入，因为在 CNN 的第一层放了一个 reshape 层，它将 784 元的输入向量变形成 1 x 28 x 28 的阵列。最开始那个 1 x 表示只有一个 channel，因为这是灰度图像，并没有 RGB 三个 channel。
接下来放一个卷积层。它包含 32 个滤波器，所以它的输出维度是 32 x 28 x 28。32 个滤波器搞出来 32 幅图像（channel），每个都是 28 x 28 大小。后面又是一个 32 个滤波器的卷积层，输出维度也是 32 x 28 x 28。
后面接上一个 Pooling 层，降降维。一个 2 x 2 的取平均值 Pooling 层，把输出维度减小了一半：32 x 14 x 14。接着是一个展平层，没有运算也没有参数，只变化一下数据形状：把 32 x 14 x 14 展平成了 6272 元向量。
该 6272 元向量送给后面一个三层的全连接神经网络。该网络的神经元个数是 1000 x 1000 x 10。两个隐藏层各有 1000 个神经元，最后的输出层有 10 个神经元，代表 10 个数字。假如第六个输出为 1，其余输出为 0，就表示网络判定这个手写数字为「5」（数字「0」占第一个输出，所以「5」占第六个输出）。数字「5」就编码成了：
训练集和测试集的数字标签都这么编码（one-hot 编码）。
全连接神经网络这部分的激活函数都采用了 Sigmoid。这出于我一个过时且肤浅的理解：用「弯弯绕」较多的 Sigmoid 给网络贡献非线性。实际上当代深度学习从生物神经的行为中得到启发，设计了其它一些表现优异的激活函数，比如单边线性 Relu。
误差函数采用均方误差 mse。优化算法采用 rmsprop，这是梯度下降的一个变体。它动态调整学习速率 LR。训练过程持续 10 轮。注意这里 10 轮不是指当前解在解空间只运动 10 步。一轮是指全部 31500 个训练样本都送进网络迭代一次。每次权值更新以 32 个样本为一个 batch 提交给算法。下图展示了随着训练，mse 的下降情况：
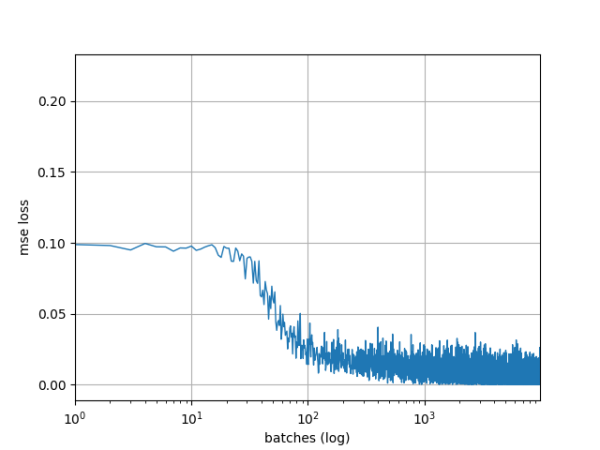
图 15
下图是分类正确率随着训练的变化情况：
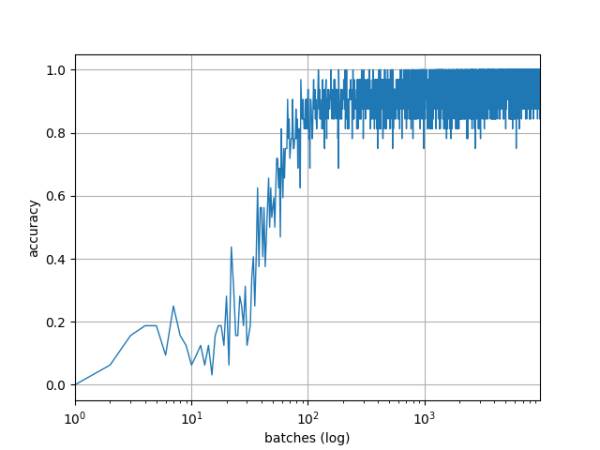
图16
该 CNN 在测试集上的正确率（accuracy）是 96.7%，各数字的准确率 / 召回率 / f1-score 如下：
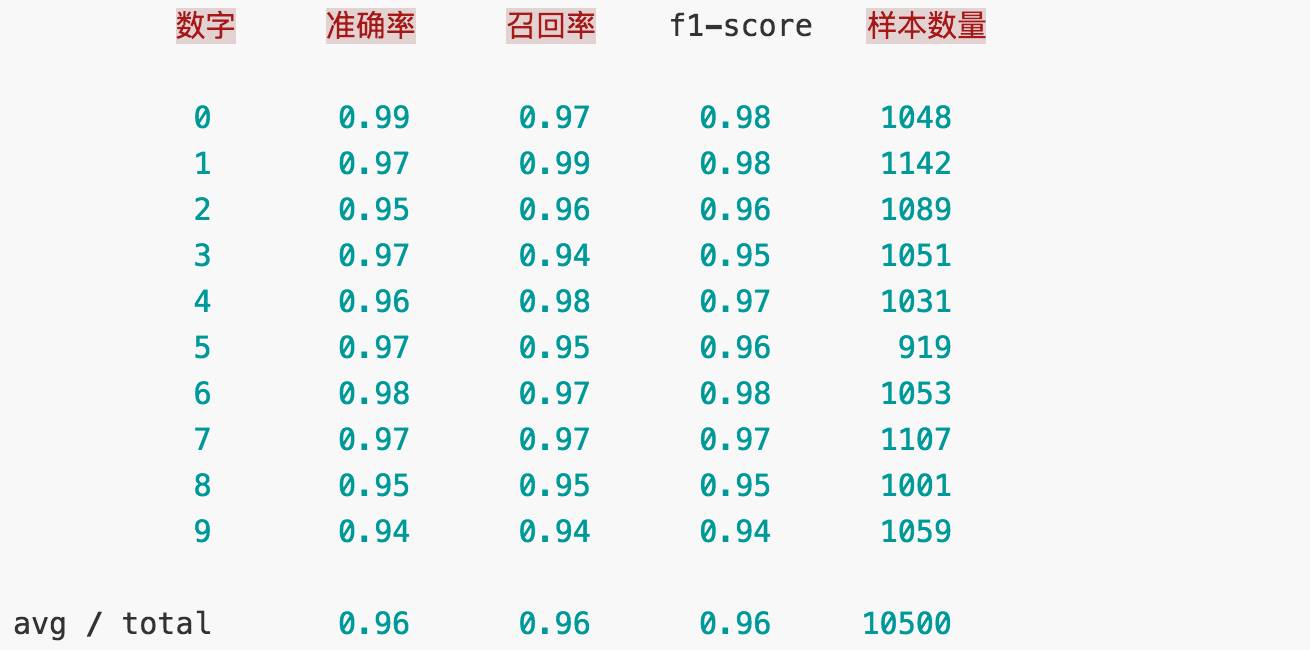
该 CNN 对测试集 10 种数字分类的混淆矩阵为：
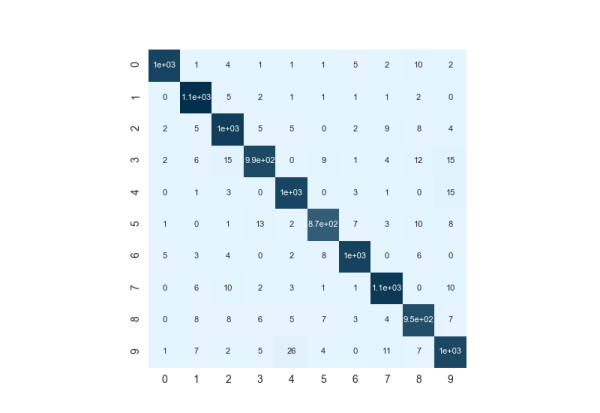
图17
训练完成神经网络后，最有趣的是将其内部权值以某种方式展现出来。看着那些神秘的、不明所以的连接强度最后竟产生表观上有意义的行为，不由让我们联想起大脑中的神经元连接竟构成了我们的记忆、人格、情感 ... 引人遐思。
在 CNN 上就更适合做这种事情。因为卷积层训练出来的是滤波器。用这些滤波器把输入图像滤一滤，看看 CNN 到底「看到」了什么。下图用第一、二卷积层的 32 个滤波器滤了图 13 第 8 行第 8 列的那个手写数字「6」。32 个 channel 显示如下：
图 18
图 19
其中有些把边缘高亮（输出值较大），有些把「6」的圈圈高亮，等等。这些就是 CNN 第一步滤波后「看到」的信息。再经过后面的各神经层，抽象程度逐层提高，它就这样「认出」了手写数字。
最后把代码附上。CNN 使用的是 keras 库。数据集来自 kaggle ：https://www.kaggle.com/c/digit-recognizer/data。
import pandas as pd
from keras.models import Sequential
from keras.layers import Dense, Flatten, Reshape, AveragePooling2D, Convolution2D
from keras.utils.np_utils import to_categorical
from keras.utils.visualize_util import plot
from keras.callbacks import Callback
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, accuracy_score, confusion_matrix
class LossHistory(Callback):
def __init__(self):
Callback.__init__(self)
self.losses = []
self.accuracies = []
def on_train_begin(self, logs=None):
pass
def on_batch_end(self, batch, logs=None):
self.losses.append(logs.get('loss'))
self.accuracies.append(logs.get('acc'))
history = LossHistory()
data = pd.read_csv("train.csv")
digits = data[data.columns.values[1:]].values
labels = data.label.values
train_digits, test_digits, train_labels, test_labels = train_test_split(digits, labels)
train_labels_one_hot = to_categorical(train_labels)
test_labels_one_hot = to_categorical(test_labels)
model = Sequential()
model.add(Reshape(target_shape=(1, 28, 28), input_shape=(784,)))
model.add(Convolution2D(nb_filter=32, nb_row=3, nb_col=3, dim_ordering="th", border_mode="same", bias=False, init="uniform"))
model.add(Convolution2D(nb_filter=32, nb_row=3, nb_col=3, dim_ordering="th", border_mode="same", bias=False, init="uniform"))
model.add(AveragePooling2D(pool_size=(2, 2), dim_ordering="th"))
model.add(Flatten())
model.add(Dense(output_dim=1000, activation="sigmoid"))
model.add(Dense(output_dim=1000, activation="sigmoid"))
model.add(Dense(output_dim=10, activation="sigmoid"))
with open("digits_model.json", "w") as f:
f.write(model.to_json())
plot(model, to_file="digits_model.png", show_shapes=True)
model.compile(loss="mse", optimizer="rmsprop", metrics=["accuracy"])
model.fit(train_digits, train_labels_one_hot, batch_size=32, nb_epoch=10, callbacks=[history])
model.save_weights("digits_model_weights.hdf5")
predict_labels = model.predict_classes(test_digits)
print(classification_report(test_labels, predict_labels))
print(accuracy_score(test_labels, predict_labels))
print(confusion_matrix(test_labels, predict_labels))
五、参考书目
［1］《最优化导论》（美）Edwin K. P. Chong（美）Stanislaw H. Zak
［2］《神经网络设计》（美）Martin T.Hagan（美）Howard B.Demuth（美）Mark Beale
©本文为机器之心转载文章，转载请联系本公众号获得授权。
✄------------------------------------------------
加入机器之心（全职记者/实习生）：[email protected]
投稿或寻求报道：[email protected]
广告&商务合作：[email protected]
