相濡以沫1)
——《庄子·大宗师》
I prefer to live in my own little bubble of my own reality.
——Lauren Lee Smith
我小的时候,老家那地方雨水还是非常充足的,印象中夏季在田里摸鱼是常有的事。大雨一下,哪天才停那可就说不准了。下雨天没事,我就望着雨线发呆。记得屋檐滴水总是能成绺儿的,在快落地的时候断成一个大水滴(这个观察让Strato 认识到下落是加速运动!),狠狠地砸在积水上,有时候就会有个大气泡从积水中冒出来。气泡刚产生时会四下里张望象个淘气的孩子(用行话说叫具有角动量),然后选个合适的方向飘然而去,不过没走多远就啵的一声破裂了。气泡产生了又破灭,这神奇的现象给我带来了不小的欢乐。
水中冒出的泡泡,英语叫bubble,德语叫Blase 或者干脆叫Gasblase(气泡)。动词冒泡的德语为blubbern,和英语的bubble 或古英语的bobelen一样都是象声词,由冒泡的声音而来2), 这反映了泡泡随时会破裂(ready to disrupt and collapse) 的特性。Bubble 作为动词,引申意为不断冒出来,如Oppenheimer is bubbling with ideas (奥本海默(的头脑中)不断冒出来主意)。干净的水不易起泡,而含发酵物的水或加肥皂的水却容易起泡,上面常常会飘着厚厚的泡沫。泡沫,英语为foam,德语为Schaum。人说话多了时的口边白沫,或者啤酒上方的沫,叫froth。Froth 作为动词有to blow hard 的意思,可能是强调泡沫破裂时的炸响。浮沫给人以无足轻重的印象,所以just froth 可以用来作抽象的比喻,比如辣眼睛的学术泡沫(academic froth)。Foam 和froth 的形容词形式分别为foamy和frothy。关于bubble,foam 和froth 的关系,下面这一句有助于体会:“Beer head is the frothy foam on top of beer which is produced by bubbles(啤酒头是指啤酒上部由气泡(bubble)组成的滋滋炸响的(frothy)浮沫(foam))”。拥有一个full, frothy head 是好啤酒的特征( 图1)。发酵物冒泡, 动词为effervesce (to foam up)。由肥皂或者别的洗涤剂造成的泡沫,有个英文词lather,它还特指(赛马的)汗沫;带泡沫的肥皂水, 英文名词是suds,形容词为sudsy。

图1 好啤酒的顶部(beer head)是由bubbles组成的frothy foam
在希腊神话中,爱与美之女神阿芙洛狄忒(Aphrodite,αφροδίτη),罗马神话中为维纳斯(Venus),是脚踩扇贝壳从海面的泡沫中诞生的。阿芙洛狄忒的一个别名干脆就是Aphrogeneia(αφρογενεια),foamborn,即“沫生人”。阿芙洛狄忒或者维纳斯的诞生,是西方文艺作品永恒的话题。希腊语词干αφρο为泡沫,其拉丁语转写aphro 出现在许多科学名词中,如aphrophora(沫蝉属)。沫蝉,英文叫froghopper 或spittlebug(吹沫虫),其德语名称Schaumzikaden字面上就是沫—蝉。沫蝉属包含多种蝉,其特征是幼虫生活在一个泡沫围成的窝(Schaumnest) 里( 图2)。类似地,有蜗牛会在水面之下脸朝上生活在一个自己营造的泡沫窝里,恰正是live in my own little bubble of my own reality。在大气环境或水中维持一个泡沫窝,考虑到可能发生的物理、化学过程,应该不是一件容易的事情。为什么有些动物会选择营造泡沫窝以及如何维持泡沫窝内条件的稳恒,应该是个相当有趣的研究课题。

图2 稻叶上的沫蝉
水包裹的气泡是最自然的现象,它天然地是科学研究的对象。关于单个气泡(bubble)的一个重要方程是Young—Laplace 方程,描述界面上的压差Δp 同界面能γ和界面几何之间的关系, Δp=γ(1/R1 + 1/R2),其中R1,R2是主曲率半径。对于球面来说,R1=R2。注意到常温下水—空气间的界面能高达72 mN/m,半径在毫米以下的气泡,其内外压差可是大气压量级的。这解释了在水中产生气泡的不易。加入肥皂、酒精一类的物质能显著降低水的表面能,因此有助于水泡的产生。有经验的养鱼人知道,若水面上布满泡泡,那是水太脏了。
若两个气泡相遇而结合(merge, coalesce), 其稳定构型是什么样的?全同的两个气泡结合,其相连部分是平的(没有压差),其余的部分为两个球帽,这似乎很好理解。如果尺寸不等,则小的气泡因为内压力大会部分地挤入大的气泡中去,则其稳定构型由三个球帽组成,且它们两两之间的二面角(dihedral angle)为120º (图3),半径关系为1/R1=1/r2-1/r1。这个看似合理的由观察而来的结论之数学证明,即为什么这样的构型是表面能最小的,是在这个世纪之交才完成的挑战。此外,三个球帽形的气泡可以共线,两两球帽之间的壁之间的夹角为120º;四个球帽形的气泡共享一个顶点时,则两两球帽之间的壁之间的夹角为arccos(-1/3)=109.47°。上述两个结论就是所谓的Plateau 定律。Joseph Plateau(1801—1883),比利时人,一个醉心于视觉研究和吹泡泡的人。Plateau晚年失去了视觉,据说仍指导侄子吹泡泡继续他的研究。他的长达450 页的《仅置于分子力之下的液体之静力学》是关于泡泡的名著。

图3 两个不同大小的气泡结合的稳定构型
醉心于吹泡泡的神人还有著名的开尔文爵士(Lord Kelvin,1824—1907),据说其侄女1887 年到乡下去看望他时,德高望重的老爵士就在忙着吹泡泡。泡沫的整体构型是表面积最小的。不知是否是受泡沫的启发,开尔文猜测图4 中的截角八面体(truncated octahedron。此为面心立方结构的Wigner—Seitz 单胞)的堆积,其总表面积最小,这即是所谓的开尔文猜想。1993 年,Denis Weaire 和Robert Phelan 找到了一种表面积更小的结构,从而判定开尔文猜想不成立。Weaire—Phelan结构以八个多面体为重复单元,其中6 个为14 面体,2 个为12 面体,而多面体的面,稍弯曲,为六边形和五边形(图4)。Weaire—Phelan 结构的面积比Kelvin的结构少0.3%。
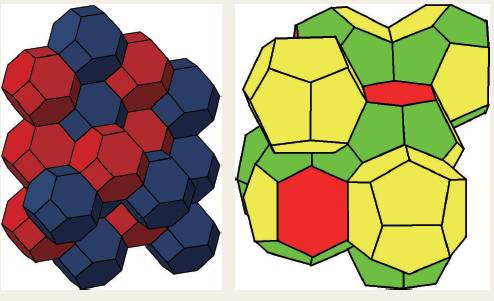
图4 充满整个三维空间的截角八面体堆积和表面积更小的Weaire—Phelan结构
泡泡的内外压力差与半径成反比,可以想见泡泡的形核不是一件容易的事,若是在固体中那就更不容易了。聚变反应和粒子注入或溅射过程会让氦气、氢气、氩气等气体在固体中团聚(cluster)成泡泡。如果固体不是那么结实且表现为各向异性,比如立方氮化铜纳米颗粒堆积的薄膜,则鼓起的气泡会表现出意想不到的海星状(图5)。

图5 Cu3N薄膜的表面形貌。因为氩气聚集的气泡,薄膜表面鼓起了五瓣的海星状隆起
泡泡不仅提供很多有趣的研究对象,比如泡泡的结冰(图6)和泡泡在液体中的运动(图7),它还为物理研究提供灵感。气泡存在于液体中,可以看作是液体的缺失,或者说缺失(void,hole)也是一种存在。由此,能量空间中(或者量子态上)缺失的一个带负电荷电子也可以看作是一个带正电荷的粒子?这个奇怪的念头导致了正电子概念的产生,进而有了反粒子和反物质的概念。在固体物理语境中,一段几乎连续的能量(能带)对应的状态如果缺乏电子的占据,那对应带正电荷的载流子,即空穴(hole)。如同水中泡泡的运动不可以仅仅看作是水受重力运动的某种等价描述,霍尔效应会告诉我们空穴也不仅仅是电子之集体运动的某种等价描述——空穴和电子还真是两类载流子。肥皂泡里的学问,可不能小觑。

图6 一个结冰的泡泡(frosted bubble or freezing bubble)

图7 水中的气泡为我们提供了空穴模型(hole model)
在许多场合,泡泡的发生却是不受欢迎的,甚至会导致严重的问题。于是,抑制泡泡的发生就成了必要。能够抑制某种液体中气泡发生的添加剂称为anti-foamer或者defoamer。
如果泡沫的壁有足够的刚性,那泡沫就可以拿来当材料用。蜂窝就是典型的泡沫材料(foam materials)。蜂窝结构本来就是bubble physics 或foam physics 的关切对象,其是符合用料最少原理的。当然,泡沫结构可能还有减振、隔热、吸声等效果,因此泡沫材料的使用大行其道且意义深远。一个简单的例子是隔热、减振的泡沫塑料的使用,它让远方的人们能尝到大闸蟹的美味,也让其它地方的螃蟹有机会到大闸蟹的故乡洗个澡后就能拥有大闸蟹的身份。
满世界跑着的金属制运输工具,如飞机、火车、汽车等,基本上都是在忙着运输它们自己,因为其中装载的人、货之重量只占少部分甚至是可以忽略不计的。如果能够减轻其自重,就可以大大降低运输能耗。将金属加工成泡沫结构,是解决此问题的思路之一。金属泡沫(图8)不仅自重大幅减少,也许同时还拥有其它的有益性能,比如热、电绝缘、有效吸收撞击能量等等。不幸的是,液态金属的表面张力太大,研制出有效的用于制备金属泡沫的发泡剂(foaming agent)不是一件容易的事。

图8 用TiH2-x 作发泡剂制作的金属铝泡沫
量子泡沫(quantum-foam), 又叫时空泡沫(spacetime foam),这个概念是物理学家惠勒(John Wheeler,1911—2008)1955 年制造的产品。根据量子场论,不确定性原理允许粒子—反粒子对不停地产生和湮灭,即存在能量的大幅涨落。又根据广义相对论,能量的大幅涨落足以引起时空对平直时空的偏离。由此,“one can image”时空不是光滑的,而是由小的、不停变化的区域组成,在其中时间和空间是不定的(not definite)。存在量子涨落的时空, 其结构是类泡沫的(foamlike structure),或者说of foamy character,此之谓时空泡沫。据说泡沫状的时空会限制测量距离的精度(实在是想多了。这肯定是不做测量的人的物理), 因为这些量子泡泡(quantum bubbles) 的尺寸在剧烈涨落。
对于这个所谓基于不确定性原理与广义相对论的引力时空量子理论的结论,完全不必当真。量子场论中涉及的虚粒子对的能量不足以引起足够的时空弯曲,所谓的量子泡沫只是凭空想象的虚粒子产生—湮灭过程在极小时空尺度上的效果。目前人们还没有找到如何构造一个自洽的量子引力理论的方法,也没有粒子尺度上时空结构的具体图像或定义。这个量子泡沫的概念不过徒具吸引眼球的功能罢了。往深处说,量子力学也没什么不确定性原理,不仅对关系式ΔxΔp≥ℏ/2的诠释常常是错误的、歪曲性的,甚至在量子力学的语境中时间是参数, ΔEΔt≥ℏ/2 根本就不存在。量子力学谈论时间(参数)和空间(位置算符),但不谈论时空。量子泡沫之类的概念,至少到目前为止还没带来任何有益的对物理学的理解。其实,量子泡沫还真不是什么新概念,很久很久以前,喜欢吹肥皂泡的开尔文爵士就曾猜想以太是一滩泡沫(the ether is a foam)。Quantum bubble,quantum foam,以及许多挂着量子羊头的狗肉,不过是foamy & nonsensical 的呓语。这些量子理论的特征都是各说各话、支离破碎,没有章法可言。类似经典力学、热力学那样严谨的量子理论体系还没建立起来。没有扎扎实实研究过经典力学者,是不配谈量子力学的,这也是狄拉克伟大的地方而玻尔后来只能瞎诌的道理。没有严谨数学连接的理论碎片,连泡沫都算不上。
量子引力理论中还引入另外一个带泡沫的概念, spin foam (自旋泡沫?)。据说a spin foam can be viewed as a quantum history (一个自旋泡沫可以看作一段量子历史)。这些理论笔者弄不懂,此处不论。
上帝创造世界使用了最少动作原理(least action principle);蜜蜂构造巢穴用了最少用料原理;肥皂泡的结构为数学家的最小面(minimal surface) 研究提供了最直观的证明和启发。这些启发中给我印象最深的是,某些支撑所张起的肥皂膜,或者说某些给定边界条件下的minimal surface,会是这样的一类函数F(x;y→0) ≠ F(x;y = 0) 。这太难以置信了,也太有冲击力了。如果不是肥皂膜可以轻松演绎这样的结果,数学家也会忽视这种存在的可能吧。这让我想起了另一件事。对任意的时空函数φ(x;t) ,在任一固定点上都可以得到一个时间序列f (t) = F ∘ φ(x = c;t) , 比如f (t) =|φ(x = c;t)|2 。但是一般来说从f (t)却无法反演出函数φ(x;t) ,更无法一口咬定它是某种波的函数并进而大谈特谈其动力学过程。楞把一个f (t) 的信号说成是探测到了某种波φ(x;t) ,那可太缺乏说服力了。电磁波的概念,可是建立在庞大的理论(麦克斯韦方程组、波动方程)和众多可观测性质(电磁波的激励、传输、折射、衍射、反射等等)的基础上的。想从某点探测到的电磁波时序信号反演出电磁波源的信息,原理上和实践上也都不是确定无疑的。
再看一眼美丽的肥皂泡(图9),再啰嗦一句说过的话:“没有严谨数学连接的理论碎片,连泡沫都算不上。”

图9 予人类以无限灵感的肥皂泡沫
1) 这一段全文为“泉涸,鱼相与处于陆,相呴以湿,相濡以沫,不如相忘于江湖。与其誉尧而非桀也,不如两忘而化其道。”庄周自己不愧为大宗师。那些拘泥于什么波粒二象性的人们,能理解庄子的“两忘而化其道”吗?
2) Bubble 的正确发音我以为就是“啵啵”, 试想象一下婴儿努嘴吐泡泡的样子。由bubble 人们还造出了zubble和wubble等词。Zubble 是人造材料吹成的彩色bubble,泡泡破裂后其中颜料不会留下污渍。
















