【推荐】条条大路通罗马LS-GAN：把GAN建立在Lipschitz密度上

那这两种GAN有没有什么联系呢？作为LS-GAN的作者，笔者就带大家一览WGAN和LS-GAN本质和联系。

GAN前传和“无限的建模能力”

熟悉经典GAN的读者都知道，GAN是一种通过对输入的随机噪声 z （比如高斯分布或者均匀分布），运用一个深度网络函数G( z )，从而希望得到一个新样本，该样本的分布，我们希望能够尽可能和真实数据的分布一致（比如图像、视频等）。

在证明GAN能够做得拟合真实分布时，Goodfellow做了一个很大胆的假设：用来评估样本真实度的Discriminator网络（下文称D-网络） 具有无限的建模能力， 也就是说不管真实样本和生成的样本有多复杂，D-网络都能把他们区分开。这个假设呢，也叫做 非参数假设 。

当然，对于深度网络来说，咱只要不断的加高加深，这还不是小菜一碟吗？深度网络擅长的就是干这个的么。

但是，正如WGAN的作者所指出的，一旦真实样本和生成样本之间重叠可以忽略不计（这非常可能发生，特别当这两个分布是低维流型的时候），而又由于D-网络具有非常强大的无限区分能力，可以完美地分割这两个无重叠的分布，这时候，经典GAN用来优化其生成网络（下文称G-网络）的目标函数--JS散度-- 就会变成一个常数！

我们知道，深度学习算法，基本都是用梯度下降法来优化网络的。一旦优化目标为常数，其梯度就会消失，也就会使得无法对G-网络进行持续的更新，从而这个训练过程就停止了。这个难题一直一来都困扰这GAN的训练，称为 梯度消失 问题。

WGAN来袭

为解决这个问题，WGAN提出了取代JS散度的Earth-Mover（EM）来度量真实和生成样本密度之间的距离。该距离的特点就是，即便用具有无限能力的D-网络完美分割真实样本和生成样本,这个距离也不会退化成常数，仍然可以提供梯度来优化G-网络。不过WGAN的作者给出的是定性的解释，缺少定量分析，这个我们在后面解释LS-GAN时会有更多的分析。

现在，我们把这个WGAN的优化目标记下来，下文我们会把它跟本文的主角LS-GAN 做一番比较。

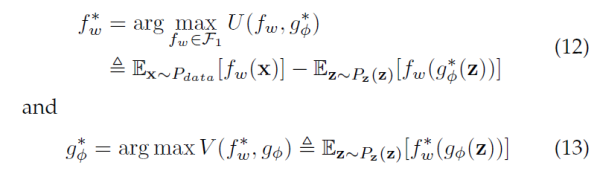
这里 f-函数和 g-函数 分别是WGAN的批评函数(critics)和对应的G-网络。批评函数是WGAN里的一个概念，对应GAN里的Discriminator。该数值越高，代表对应的样本真实度越大。

好了，对WGAN就暂时说到这里。总结下，由于假设中的 无限建模能力， 使得D-网络可以完美分开真实样本和生成样本，进而JS散度为常数；而WGAN换JS散度为EM距离，解决了优化目标的梯度为零的问题。

不过细心的读者注意到了，WGAN在上面的优化目标（12）里，有个对f-函数的限定：它被限定到所谓的Lipschitz连续的函数上的。那这个会不会影响到上面对模型 无限建模能力的 假设呢？

其实，这个对f-函数的Lipschitz连续假设，就是沟通LS-GAN和WGAN的关键，因为LS-GAN就是为了限制GAN的 无限建模能力 而提出的。

熟悉机器学习原理的朋友会知道，一提到 无限建模能力， 第一反应就应该是条件反应式的反感。为什么呢？无限建模能力往往是和过拟合，无泛化性联系在一起的。

仔细研究Goodfellow对经典GAN的证明后，大家就会发现，之所以有这种无限建模能力假设，一个根本原因就是GAN没有对其建模的对象--真实样本的分布--做任何限定。

换言之，GAN设定了一个及其有野心的目标：就是希望能够对各种可能的真实分布都适用。结果呢，就是它的优化目标JS散度，在真实和生成样本可分时，变得不连续，才使得WGAN有了上场的机会，用EM距离取而代之。

所以，某种意义上， 无限建模能力正是一切麻烦的来源。 LS-GAN就是希望去掉这个麻烦，取而代之以“按需分配”建模能力。

LS-GAN和“按需分配”的建模能力

好，让我们换个思路，直接通过限定的GAN的建模能力，得到一种新的GAN模型。这个就是LS-GAN了。我们先看看LS-GAN的真容：

这个是用来学习损失函数的目标函数。我们将通过最小化这个目标来得到一个“损失函数" (L，下文称之为L-函数)。L-函数在真实样本上越小越好，在生成的样本上越大越好。

另外，对应的G-网络，通过最小化下面这个目标实现：

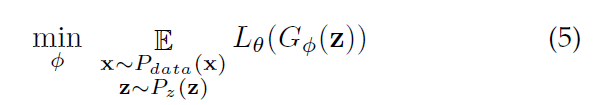
这里注意到，在公式（6）中，对L-函数的学习目标 S中的第二项，它是以真实样本 x 和生成样本ZG的一个度量为 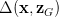各自L-函数的目标间隔，把 x 和ZG分开。

这有一个很大的好处：如果生成的样本和真实样本已经很接近，我们就不必要求他们的L-函数非得有个固定间隔，因为，这个时候生成的样本已经非常好了，接近或者达到了真实样本水平。

这样呢，LS-GAN就可以集中力量提高那些距离真实样本还很远，真实度不那么高的样本上了。这样就可以更合理使用LS-GAN的建模能力。在后面我们一旦限定了建模能力后，也不用担心模型的生成能力有损失了。这个我们称为“ 按需分配 ”。

上图就是对LS-GAN这种对建模能力”按需“分配的图示。

有了上面的准备，我们先把LS-GAN要建模的样本分布限定在Lipschitz 密度上，即如下的一个假设：

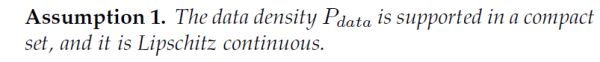
那么什么是Lipschitz密度了？简而言之，Lipschitz密度就是要求真实的密度分布不能变化的太快。密度的变化随着样本的变化不能无限地大，要有个度。不过这个度可以非常非常地大，只要不是无限大就好。

好了，这个条件还是很弱地，大部分分布都是满足地。比如，你把一个图像调得稍微亮一些，它看上去仍然应该是真实的图像，在真实图像中的密度在Lipschitz假设下不应该会有突然地、剧烈地变化。不是吗？

然后，有了这个假设，我就能证明LS-GAN，当 把L-函数限定在Lipschitz连续的函数类 上，它得到地生成样本地分布和真实样本是完全一致！

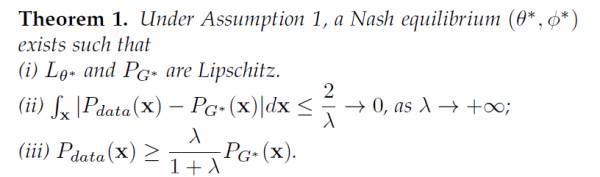
前面我们说了，经典GAN事实上对它生成的样本密度没有做任何假设，结果就是必须给D-网络引入无限建模能力，正是这种能力，在完美分割真实和生成样本，导致了梯度消失，结果是引出了WGAN。

现在，我们把LS-GAN限定在Lipschitz密度上，同时限制住L-函数的建模能力到Lipschitz连续的函数类上，从而证明了LS-GAN得到的生成样本密度与真实密度的一致性。

那LS-GAN和WGAN又有什么关系呢？

细心的朋友可能早注意到了，WGAN在学习f-函数是，也限定了其f-函数必须是Lipschitz连续的。不过WGAN导出这个的原因呢，是因为EM距离不容易直接优化，而用它的共轭函数作为目标代替之。

也就是说，这个对f-函数的Lipschitz连续性的约束，完全是“技术”上的考虑，没有太多物理意义上的考量。

而且，WGAN的作者也 没有 在他们的论文中证明：WGAN得到的生成样本分布，是和真实数据的分布是一致的。不过，这点在我们更新的预印本中给出了明确的证明，如下：

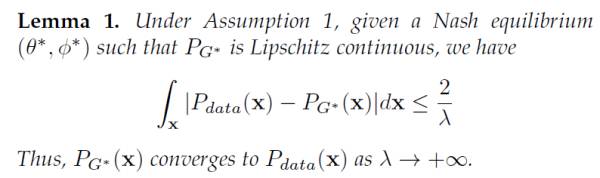
换言之：我们证明了，WGAN在对f-函数做出Lipschitz连续的约束后，其实也是将生成样本的密度假设为了Lipschiz 密度。这点上，和LS-GAN是一致的！两者都是建立在Lipschitz密度基础上的生成对抗网络。

好了，让我们把LS-GAN和WGAN对L-函数和f-函数的学习目标放在一起仔细再看一看：

LS-GAN ：

WGAN ：

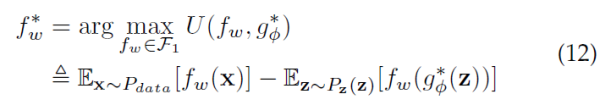
形式上 来看，LS-GAN和WGAN也有很大区别。WGAN是通过最大化f-函数在真实样本和生成样本上的期望之差实现学习的，这种意义上，它可以看做是一种使用“一阶统计量"的方法。

LS-GAN则不同。观察LS-GAN优化目标的第二项，由于 非线性 ()+的函数的存在，使得我们无法把L-函数分别与期望结合，像WGAN那样得到一阶统计量。因为如此，才使得LS-GAN与WGAN非常不同。

LS-GAN可以看成是使用 成对 的（Pairwise）“真实/生成样本对”上的统计量来学习f-函数。这点迫使真实样本和生成样本必须相互配合，从而更高效的学习LS-GAN。

如上文所述，这种配合，使得LS-GAN能够按需分配其建模能力：当一个生成样本非常接近某个真实样本时，LS-GAN就不会在过度地最大化他们之间L-函数地差值，从而LS-GAN可以更有效地集中优化那些距离真实样本还非常远地生成样本，提高LS-GAN模型优化和使用地效率。

梯度消失问题

那LS-GAN是否也能解决经典GAN中的 梯度消失 问题呢？即当它的L-函数被充分训练后，是否对应的G-网络训练目标仍然可以提供足够的梯度信息呢？

我们回顾下，在WGAN里，其作者给出G-网络的训练梯度，并证明了这种梯度在对应的f-函数被充分优化后，仍然存在。

不过，仅仅梯度存在这点并不能保证WGAN可以提供足够的梯度信息训练 G-网络。为了说明WGAN可以解决梯度消失问题，WGAN的作者宣称：“G-网络的训练目标函数”在对其网络链接权重做限定后， 是 接近或者最多线性 的。这样就可以避免训练目标函数饱和，从而保证其能够提供充足的梯度训练G-网络。

好了，问题的关键时为什么G-网络的训练目标函数是接近或者最多 线性 的，这点WGAN里并没有给出定量的分析，而只有大致的定性描述，这里我们引用如下：