回报率850%? 这个用Python优化的比特币交易机器人简直太烧脑了...

上个月，AI 工程师 Adam King 结合人工智能在预测方面得天独厚的优势，提出使用深度强化学习构建加密货币自动交易的程序。在展示模型中，程序的收益率竟达到了惊人的 60 倍（只讨论技术，无关投资建议）。

但在当时，这个展示模型略显粗糙。虽然能获得收益，但它并不稳定。使用它可能让你赚得盆满钵盈，也有可能让你赔得一无所有，颇有些“富贵险中求”的意味。

不稳定的问题一直困扰着 Adam 小哥，经过一个月的蛰伏，小哥提出将特征工程和贝叶斯优化两大杀器引入模型。这些改进会奏效么？收益率又能提升多少呢？一起来看看 Adam 小哥的最新力作吧！

本篇文章的目的是测试当下最先进的深度强化学习技术是否能与区块链相结合，创造出一个可以盈利的比特币自动交易智能体。 目前看来业界都还没有意识到深度强化学习在自动交易方面强大的潜力，反而认为它并不是一个“能用来构建交易算法的工具”。不过，深度学习领域的最新进展已经表明，在同一个问题上强化学习智能体通常能够比普通的监督学习智能体学习到更多的特征。

出于这个原因，我做了相关的实验来探究基于深度强化学习的交易智能体究竟能达到怎样的收益率，当然了， 结果也可能会是深度强化学习有着很强的局限性以至于并不适合做交易智能体，但不去尝试谁又知道结果如何呢？

首先，我们将会 改进深度强化学习模型的策略网络 （ policy network ）并使输入数据变得平稳，以便交易智能体能在很少的数据中学习到更多的特征。

接下来，我们将使 用当下先进的特征工程方法来改善交易智能体的观察空间 ，同时微调交易智能体的奖励函数（ reward function ）以帮助它发现更好的交易策略。

最后，在训练并测试交易智能体获得的收益率之前，我们将 使用贝叶斯优化的方法来寻找能最大化收益率的超参数。

前方高能，系好安全带，让我们开始这场干货满满的探索之旅吧。

关于深度强化学习模型的改进

之前，我们已经实现了深度强化学习模型的基本功能，

GitHub 地址：

https://github.com/notadamking/Bitcoin-Trader-RL

当务之急是 提高深度强化学习智能体的盈利能力 ，换句话说就是要对模型进行一些改进。

循环神经网络（Recurrent Neural Network，RNN）

我们需要做的第一个改进就是 使用循环神经网络来改进策略网络 ，也就是说，使用长短期记忆网络（ Long Short-Term Memory ，LSTM ）网络代替之前使用的多层感知机（ Multi-Layer Perceptron，MLP ）网络。由于循环神经网络随着时间的推移可以一直保持内部状态，因此我们不再需要滑动“回顾窗口“来捕捉价格变动之前的行为，循环神经网络的循环本质可以在运行时自动捕捉这些行为。在每个时间步长中，输入数据集中的新一个数据与上一个时间步长的输出会被一起输入到循环神经网络中。

因而长短期记忆网络可以一直维持一个内部状态。在每个时间步长中，智能体会新记住一些新的数据关系，也会忘掉一些之前的数据关系，这个内部状态也就会随之更新。

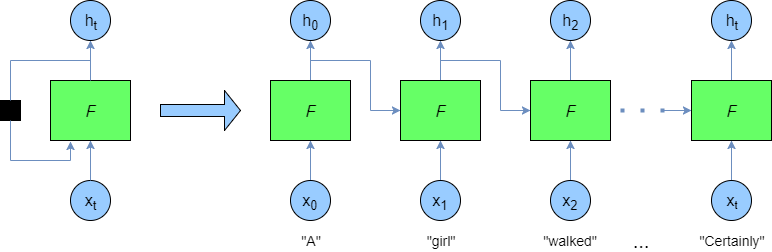
循环神经网络会接收上一个时间步长的输出

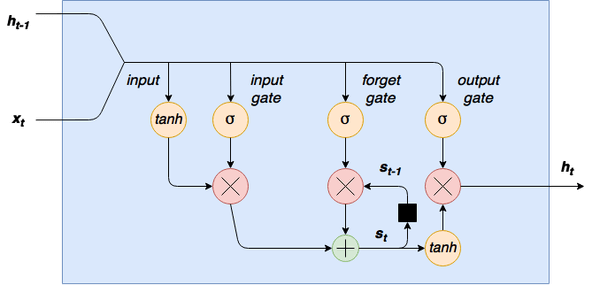
循环神经网络如何处理上一个时间步长的输出与这一个时间步长的输入

长短期记忆网络实现代码 LSTM_model.py

介于循环神经网络对于内部状态得天独厚的优势，在这里，我们 使用长短期记忆网络策略更新了近端策略优化 PPO2 模型 。

数据平稳性

之前，我曾指出比特币交易的数据是非平稳的（Non-Stationary，即存在一些趋势，而不能仅仅看作是随机的波动），因此，任何机器学习模型都难以预测未来。

平稳时间序列是平均值，方差和自相关系数（与其自身的滞后相关）都恒定的时间序列。

而且， 加密货币价格的时间序列有着很明显的趋势和季节效应（季节效应是指与季节相关联的股市非正常收益，是股市中的一种“异像”，是与市场有效性相悖的情况） ，这两者都会影响算法对时间序列预测的准确率，所以在这里，我们需要使用差分和变换的方法来处理输入数据，从现有的时间序列中构建一个正常的数据分布来解决这个问题。

从原理上来说，差分过程就是给任意两个时间步长内加密货币币价的导数（即收益率）做差值。在理想情况下，这样做可以消除输入时间序列中存在的趋势，但是，差分处理对季节效应并不奏效，处理后的数据仍然具有很强的季节效应。这就需要我们 在差分处理之前进行对数处理来消除它，经过这样的处理最终我们会得到平稳的输入时间序列 ，如下方右图所示。

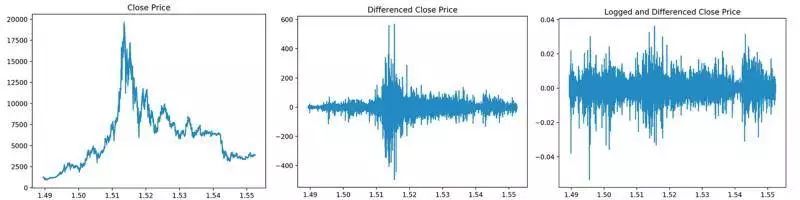
从左到右分别为：

加密货币的收盘价，差分处理后的收盘价，对数处理和差分处理后的收盘价

对数处理和差分处理的代码 diff_and_log_time_series.py

处理后的输入时间序列平稳性如何，我们可以使用增广迪基-福勒检验（ Augmented Dickey-Fuller test ）验证一下。

运行以下代码：

增广迪基-福勒检验的代码 adfuller_test.py

我们得到的 p 值为 0.00 ，这意味着我们 拒绝假设检验中的零假设并确认处理后的输入时间序列是平稳的 。

我们可以运行上面的增广迪基-福勒检验代码来检验输入时间序列的平稳性。

在完成了这项工作之后，接下来我们将 使用特征工程的方法进一步优化交易智能体的观察空间 。

特征工程

为了进一步提升交易智能体的收益率，我们需要做一些特征工程。

特征工程是使用该领域知识来生成额外的输入数据从而优化机器学习模型的过程。

具体到交易智能体，我们将 在输入数据集中添加一些常见且有效的技术指标，以及 Python 数据分析程序库 StatsModels 中季节效应预测模型 SARIMAX 的输出 。这些技术指标会为我们的输入数据集带来一些相关的，但可能会滞后的信息，这些信息能大大提升交易智能体预测的准确性。这些优化方法的组合可以为交易智能体提供一个非常好的观察空间，让智能体学习到更多的特征，从而获得更多的收益。

技术分析

为了选择技术指标，我们将 比较 Python 技术分析库 ta 中可用的所有 32 个指标（ 58 个特征）的相关性 。可以使用数据分析工具 pandas 来计算相同类型的各个指标（如动量，体积，趋势，波动率）之间的相关性，然后在每种类型中仅选择最不相关的指标作为特征。这样，就可以在不给观察空间带来过多噪音干扰的情况下，最大程度地发掘这些技术指标的价值。

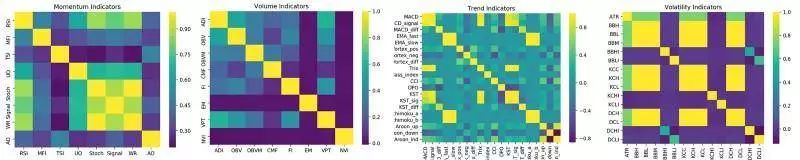
使用 Python 高级可视化库 seaborn 做出的比特币数据集上技术指标相关性的热力图

结果显示，波动率指标以及一些动量指标都是高度相关的。在删除所有重复的特征（每个类型中相关性的绝对平均值大于 0.5 的特征）之后，我们将剩余的 38 个技术特征添加到交易智能体的观察空间中。

在代码中，我们需要 创建一个名为 add_indicators（添加指标）的函数来将这些特征添加到数据帧中 ，为了避免在每个时间步长中重复计算这些特征，我们只在交易智能体环境初始化的过程中调用 add_indicators 函数。

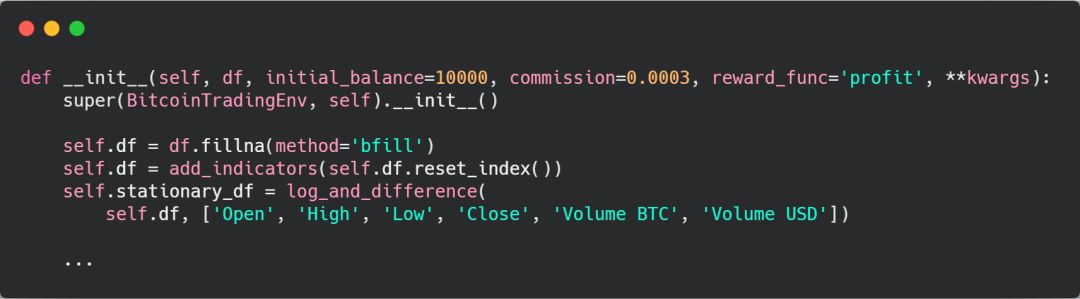
交易智能体环境初始化的代码 initialize_env.py

在这里，初始化交易智能体环境，在进行数据平稳性处理之前将特征添加到了数据帧中。

统计分析

接下来我们需要添加预测模型。

由于季节效应自回归移动平均模型（Seasonal Auto Regressive Integrated Moving Average，SARIMA）可以在每个时间步长中快速计算价格的预测值，在平稳数据集中运算非常准确，因此我们使用它来进行加密货币币价预测。

除了上述这些优点之外，该模型实现起来非常简单，它还可以给出预测值的置信区间，通常情况下这比单独给出一个预测值能提供更多的信息。就比如说，当置信区间较小时，交易智能体就会更相信这个预测值的准确性，当置信区间很大时交易智能体就知道要承担更大的风险。

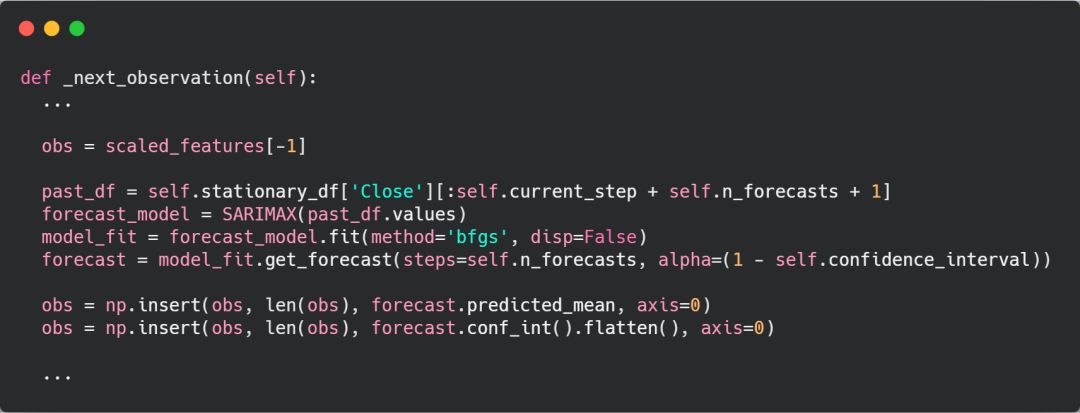
加入 SARIMA 预测模型的代码 add_sarimax_predictions.py

这里我们将 SARIMAX 预测模型和置信区间添加到交易智能体的观察空间中。

现在我们 已经使用性能更好的循环神经网络更新了策略，并使用特征工程的方法改进了交易智能体的观察空间 ，是时候优化其他的部分了。

奖励优化

有些人可能会觉得，之前文中的奖励函数（即奖励资产总价值不断增加）已经是最好的解决方案了，但是，通过进一步的研究我发现奖励函数还有提升的空间。 虽然我们之前使用的简单奖励函数已经能够获得收益，但它给出的投资策略非常不稳定，往往会导致资产的严重损失。 为了改善这一点，除了考虑利润的增加以外，我们还需要考虑其他奖励的指标。

奖励指标的一个简单改进就是， 不仅仅奖励在比特币价格上涨时持有比特币带来的利润，还奖励在比特币价格下跌时抛售比特币而避免的损失 。就比如说，我们可以奖励智能体买入比特币而总资产增加的行为，以及卖出比特币避免总资产减少的行为。

虽然这种奖励指标在提高收益率方面非常出色，但这样做并没有考虑到高回报带来的高风险。 投资者早已发现这种简单投资策略背后存在的漏洞，并将其改进成一种风险可调节的奖励指标。

基于波动率的奖励指标

这种风险可调节的奖励指标中的典型就是夏普比率（Sharpe Ratio，又被称为夏普指数）。它计算的是特定时间段内投资组合的超额收益与波动性的比率。具体的计算公式如下：

夏普比率的计算公式：（投资组合的收益-大盘的收益）/投资组合的标准差

从公式中我们可以得出，为了保持较高的夏普比率，投资组合必须同时保证高收益和低波动性（也就是风险）。

作为一种奖励指标，夏普比率经受住了时间的考验，但它对于自动交易智能体来说并不是很完美，因为它会对上行标准差（ upside volatility ）产生不利影响，而在比特币交易环境中有时我们需要利用上行标准差，因为上行标准差（即比特币价格疯狂上涨）通常都是很好的机会窗口。

而使用索提诺比率（ Sortino Ratio ）可以很好地解决这个问题。索提诺比率与夏普比率非常相似，只是它在风险上只考虑了下行标准差，而不是整体标准差。因此，索提诺比率并不会对上行标准差产生什么不利影响。因而我们给交易智能体的第一条奖励指标就选择索提诺比率，它的计算公式如下：

索提诺比率的计算公式：（投资组合的收益-大盘的收益）/投资组合的下行标准差

其他奖励指标

我们选择 Calmar 比率作为交易智能体的第二个奖励指标。到目前为止，我们所有的奖励指标都没有考虑到比特币币价最大回撤率（drawdown）这个关键因素。

最大回撤率是指比特币币价从价格顶峰到价格低谷之间的价值差，用来描述买入比特币后最糟糕的情况。

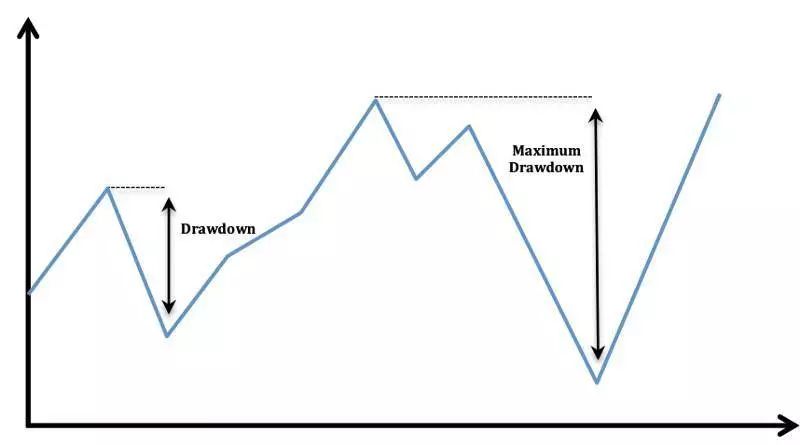
最大回撤率

为了消除最大回撤率带来的负面影响，我们需要选用可以处理这种情况的奖励指标，就比如说 选用 Calmar 比率 。该比率与夏普比率类似，只是它将分母上投资组合的标准差替换为最大回撤率。

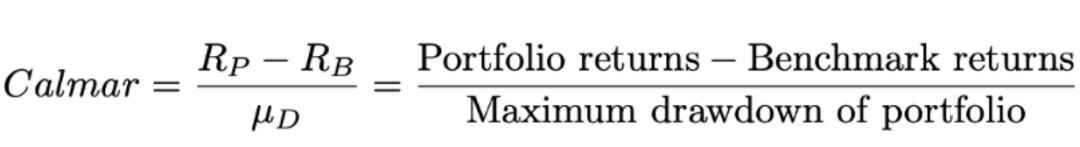
Calmar 比率的计算公式：（投资组合的收益-大盘的收益）/最大回撤率

我们最后一个奖励指标是在对冲基金行业中广泛使用的 Omega 比率。从理论上来说，在衡量风险与收益时，Omega 比率应该优于 Sortino 比率和 Calmar 比率，因为它能够在单个指标中使用收益的分布来评估风险。

计算 Omega 比率时，我们需要分别计算在特定基准之上或之下投资组合的概率分布，然后两者相除计算比率。 Omega 比率越高，比特币上涨潜力超过下跌潜力的概率就越高。

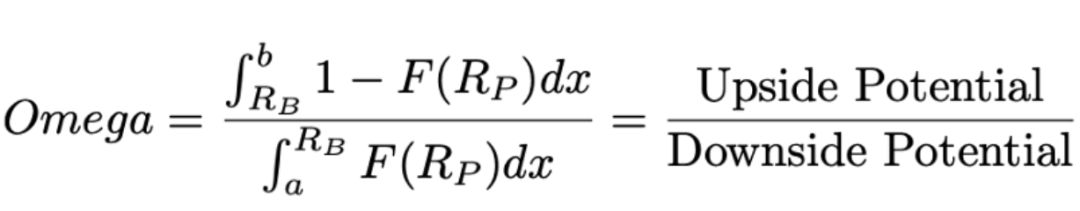
Omege 比率的计算公式

Omega 比率的计算公式看起来很复杂，不过不要担心， 在代码中实现它并不难 。

代码实现

虽然说编写每个奖励指标的代码听起来很有意思且很有挑战性，但这里为了方便大家的理解，我选择使用 Python 量化金融程序包 empyrical 来计算它们。幸运的是，这个程序包中恰好包含了我们上面定义的三个奖励指标，因而在每个时间步长中，我们只需要将该时间段内收益和大盘收益的列表发给 Empyrical 函数，它就会返回这三个比率。

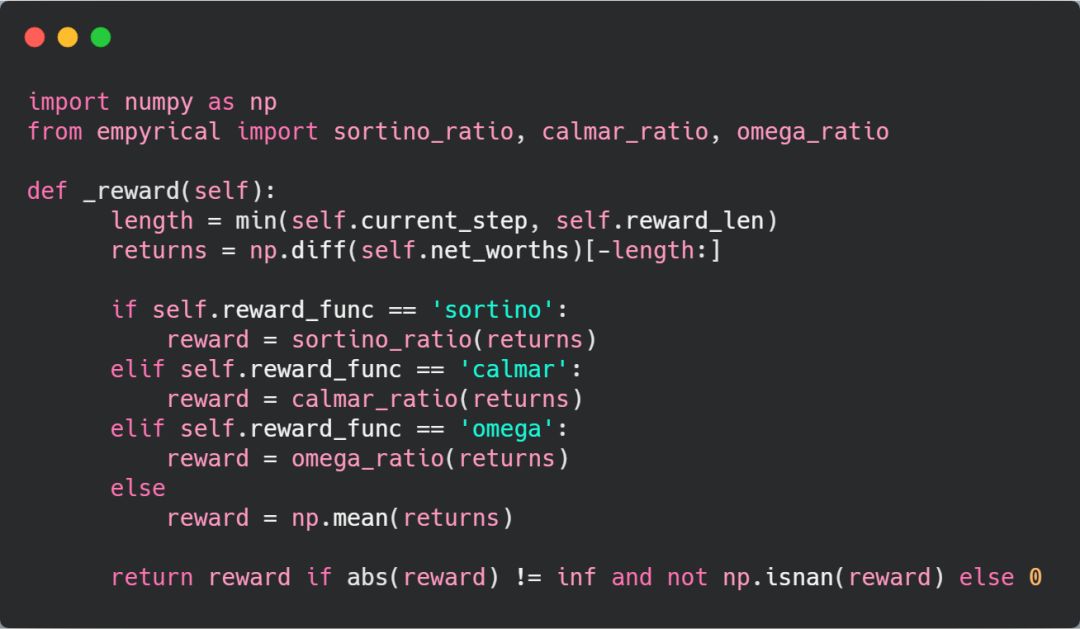
使用 empyrical 程序包计算三个奖励指标的代码 risk_adjusted_reward.py

在代码中，我们通过预先定义的奖励函数设置了每个时间步长的奖励。

到目前为止，我们已经确定了如何衡量一个交易策略的成功与否，现在是时候弄清楚 哪些指标会带来较高的收益 。我们需要将这些奖励函数输入到自动超参数优化软件框架 Optuna 中，然后使用贝叶斯优化来的方法为输入数据集寻找最优的超参数。

工具集

俗话说，好马配好鞍。任何一个优秀的技术人员都需要一套好用的工具，否则就会巧妇难为无米之炊。

但我并不是说我们要重复造轮子，我们应该学会使用程序员前辈用秃头的代价为我们开发的工具，这样他们的工作也算没有白费。 对于我们所开发的交易智能体，它要用到的最重要的工具就是自动超参数优化软件框架 Optuna ，从原理上来说，它使用了树结构的 Parzen 窗估计（Tree-structured Parzen Estimators，TPEs）来实现贝叶斯优化，而这种估计方法是可以并行化运行的，这使得我们的显卡有了用武之地，执行搜索需要的时间也会大大缩短。简而言之，

贝叶斯优化是一种搜索超参数空间以找到能最大化给定目标函数的超参数的高效解决方案。

也就是说，贝叶斯优化能够有效地改进任何黑箱模型。从工作原理上来说， 贝叶斯优化通过使用替代函数（ surrogate functions ）或是替代函数的分布对要优化的目标函数进行建模。 随着时间的推移，算法不断地检索超参数空间以找到那些能够最大化目标函数的超参数，分布的效果也会逐渐改善。

理论说了这么多，我们要如何把这些技术应用在比特币自动交易智能体中呢？从本质上来讲，我们可以使用这种技术来找到一组最优的超参数，使得智能体的收益率最高。这个过程就像是在超参数的汪洋大海中捞取一根效果最好的针，而贝叶斯优化就是带我们找到这根针的磁铁。让我们开始吧。

使用 Optuna 优化超参数并不是什么难事。

首先，我们需要 创建一个 optuna 实例 ，也就是装载所有超参数试验的容器。在每次试验中我们需要调整超参数的设置来计算目标函数相应的损失函数值。在实例初始化完成后，我们需要向其中传入目标函数然后调用 study.optimize() 函数开始优化，Optuna 将使用贝叶斯优化的方法来寻找能够最小化损失函数的超参数配置。

使用 Optuna 程序库贝叶斯优化的代码 optimize_with_optuna.py

在这个例子中， 目标函数就是在比特币交易环境中训练并测试智能体，而目标函数的损失值则定义为测试期间智能体平均收益的相反数 ，之所以给收益值加上负号，是因为平均收益越高越好，而在 Optuna 看来损失函数越低越好，一个负号刚好解决这个问题。optimize 优化函数为目标函数提供了试验对象，代码中我们可以指定试验对象中的变量设置。

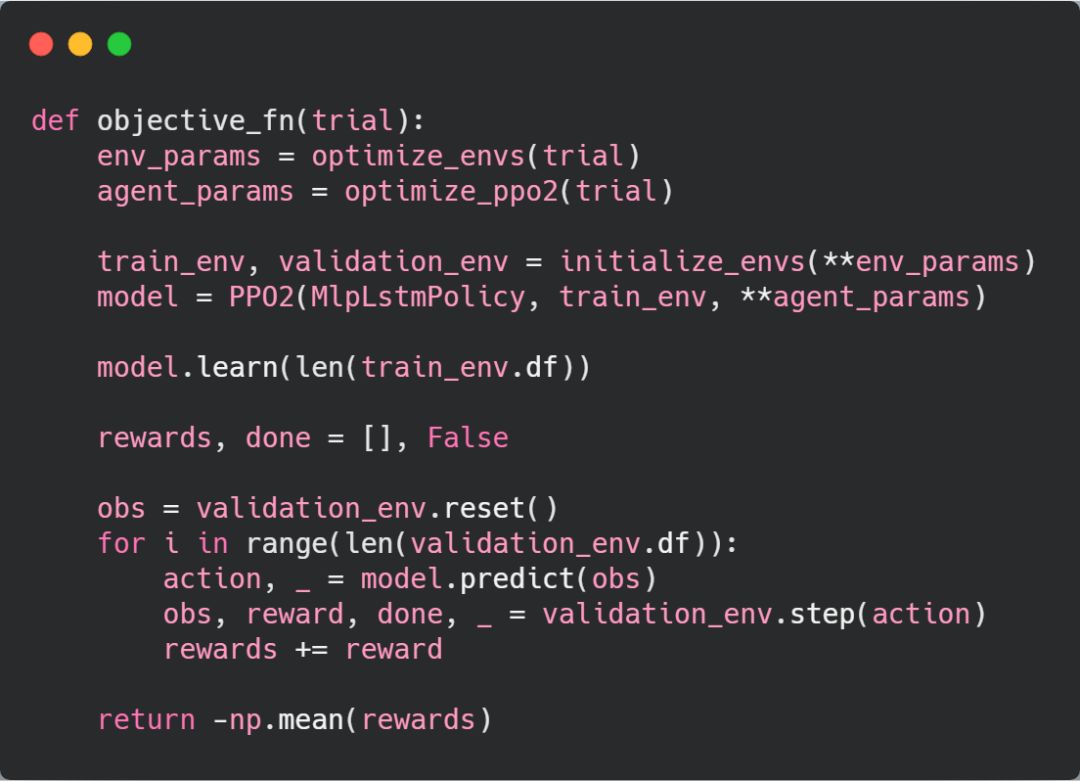
优化目标函数的代码 optimize_objective_fn.py

optimize_ppo2 优化智能体函数和 optimize_envs 优化智能体环境函数接收试验对象作为输入并返回包含要测试参数的字典。每个变量的搜索空间由 suggest 函数进行设置，我们需要在试验中调用 suggest 函数并给函数中传入指定的参数。

比如说，如果设置参数在对数尺度上服从均匀分布， 即调用函数

trial.suggest_loguniform（'n_steps'，16，2048），

相当于给函数了一个 16-2048 之间的 2 的指数次方（如16，32，64，…，1024，2048）的新浮点数。

再者，如果设置参数在普通尺度上服从均匀分布， 即调用函数

trial.suggest_uniform（'cliprange'，0.1，0.4），

相当于给函数一个 0.1 到 0.4 之间的新浮点数（如0.1，0.2，0.3，0.4）。

相信你已经看出来了其中的规律，就是这样来设置变量：

suggest_categorical（'categorical'，['option_one'，'option_two']），其中 categorical 为设置变量的策略， option_one 和 option_two 分别为变量的两个选项，在刚才的函数中这两个选项为变量的范围，弄懂了这个相信下面的代码就难不倒你了。

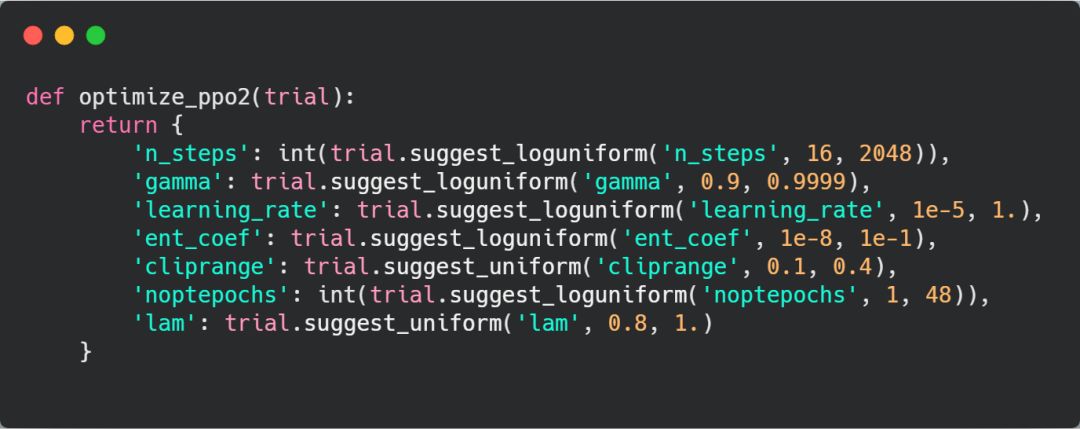
化交易智能体的代码 optimize_ppo2.py

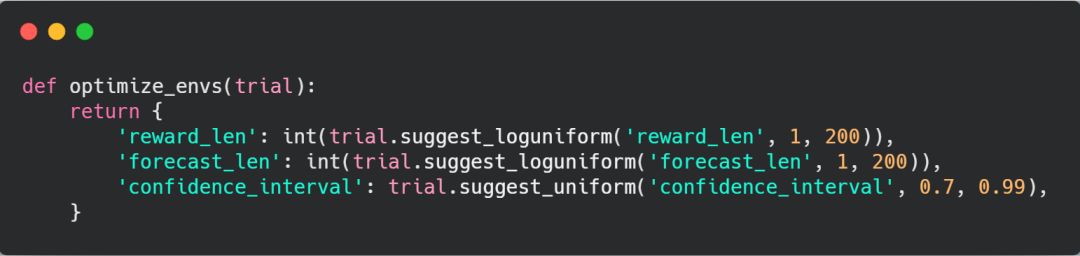
优化交易环境的代码 optimize_envs.py

代码写好后，我们 在一台高性能服务器上以 CPU/显卡协同运算的方式运行了优化函数 。在设置中，Optuna 创建了一个 SQLite 数据库，我们可以从中加载优化的实例。该实例记录了测试过程中性能最好的一次试验，从中我们可以推算出智能体交易环境中最优的超参数集。

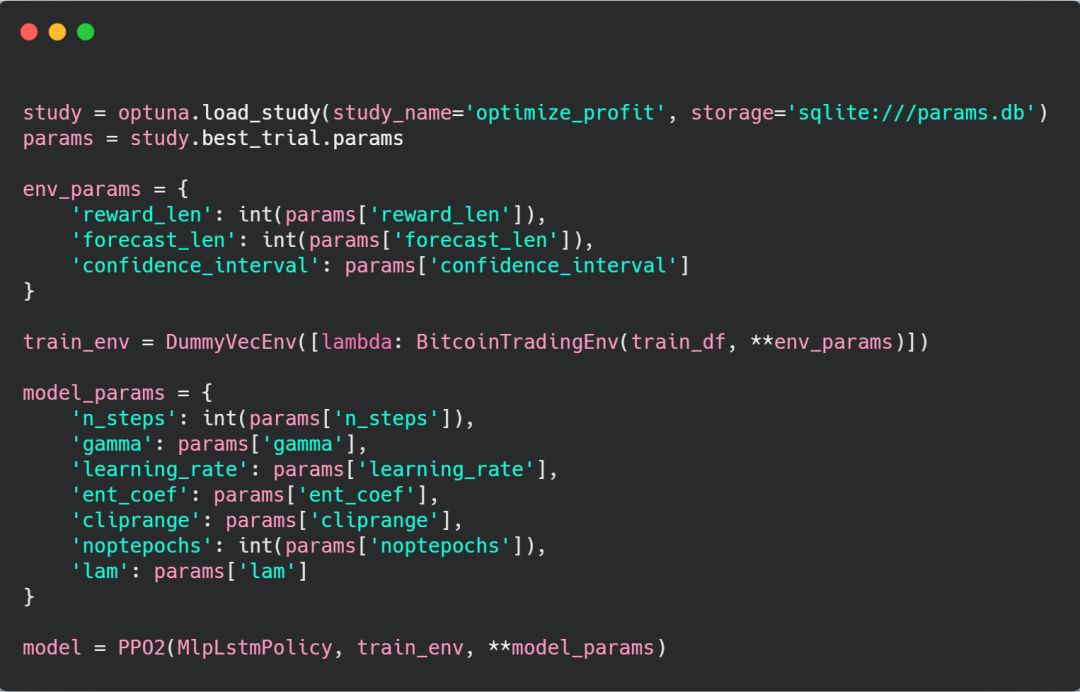
加载 optuna 实例的代码 load_optuna_study.py

到这里，我们已经改进了模型，改进了特征集，并优化了所有的超参数。 但俗话说，是骡子是马得拉出来遛遛。

那么，交易智能体在新的奖励指标下表现如何呢？

在训练过程中，我分别使用了 利润 、 Sortino 比率 、 Calmar 比率 和 Omega 比率 四个奖励指标来优化智能体。接下来我们需要在测试环境中检验哪种奖励指标训练出来的智能体收益最高，当然了，测试环境中的数据都是智能体在训练过程中从未见到过的比特币价格走势，这样保证了测试的公平性。

收益比较

在查看结果之前，我们需要知晓一个成功的交易策略是什么样的。出于这个原因，我们将针对一些常见且有效的比特币交易策略进行基准测试。令人震惊的是， 在过去的十年中一个最有效的比特币交易策略就是买入并持有，而另外两个不错的交易策略则是使用简单但有效的技术分析来生成买入/卖出信号，从而指导交易。

1、买入并持有

这种交易策略指尽可能多地购买比特币并一直持有下去（也就是区块链社区中的江湖黑话“ HODL ”）。虽然说这种交易策略并不是特别复杂，但在过去这样做赚钱的机率很高。

2、相对强弱指数分歧（Relative Strength Index（RSI） divergence ）

当相对强弱指数持续下跌且收盘价持续上涨时，这就是需要卖出的信号，而当相对强弱指数持续上涨且收盘价持续下跌时，就是需要买入的信号。

3、简单移动平均线（ Simple Moving Average，SMA ）交叉

当长期简单移动平均线超过短期简单移动平均线时，这就是需要卖出的信号，而当短期简单移动平均线超过长期简单移动平均线时，就是需要买入的信号。