这三张卡片都可以无限翻折

卡片1 每个画面四个小块

卡片2 每个画面三个小块

卡片3 平面六边形的无限翻折
把弄这些奇特的卡片同时,自然想到了两个问题
1. 这些卡片怎么实现无限翻折的?
2. 怎么利用卡片无限翻转的特性?
- 即 -
△
应用问题:
利用折纸创意制作贺卡
△
理论问题:
讨论无限翻折的原理
回应本篇标题,先解决
应用问题

如何设计折纸效果?
1. 以卡片1 为例,获取素材图

2.
Photoshop 描出素材框线
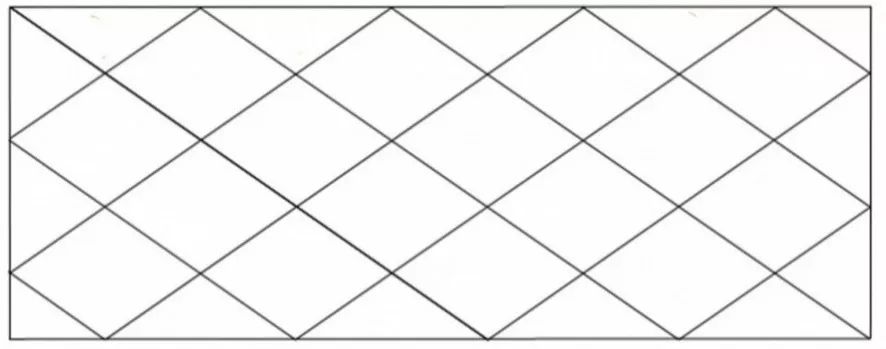
3. 菱块分为四组,每组对应一个画面
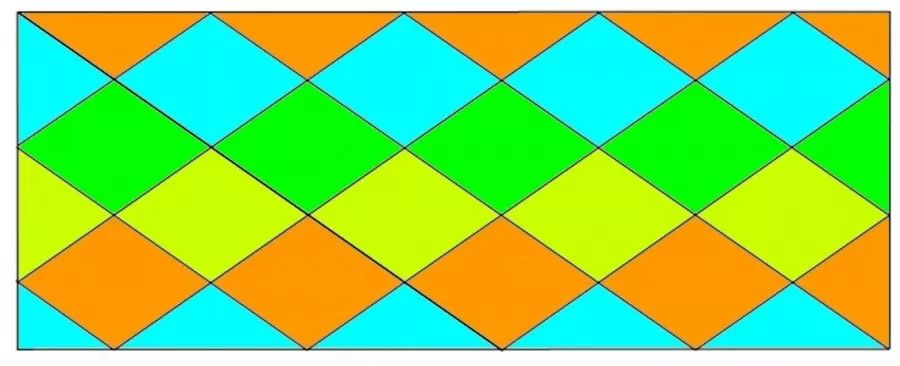
4. 分别填充图片,电子版完成

5. 打印并按框线折纸
扫描或长按二维码
查看图文教程
▼

△ 一定视觉差下,
四个菱块可组成方形

△ 巧用视觉差

视觉错觉-别盯着我
△ 按图示裁切,菱块上顶点为原图顶点

△ 成品效果

PS:图片裁切费时,多卡片制作容易忙不过来
这时候,万能工具
Python
就该登场了。

Python 有PIL,OpenCV,Scikit-Image 等丰富的图片处理库,这里主要用 skimage 库裁切图片,附参考代码:
函数代码:
from skimage import transform,io
from PIL import Image
def diamond_math(img,size,alpha=45,n=1) :
im= transform.rotate(img,alpha,resize=True)
img = transform.resize(im,size)
file = '%d.png'%n
io.imsave(file,img)
im = Image.open(file)
return im
def pil_to_ski(img,file='1.png') :
img.save(file)
img = io.imread(file)
return img
def pic_paste(img,file,size,loc) :
im = io.imread(file)
[height,width,_] = im.shape
l = min(height,width)
a = l//2-1
b = 2*a+1
im_list = [im[0:a, 0:a, :], im[0:a, a:b, :], im[a:b, a:b, :], im[a:b, 0:a, :] ]
x,y = loc
im_list2 = []
for i,pic in enumerate(im_list):
im_list2.append(diamond_math(pic,size,i*90-45,i))
for i,pic in enumerate(im_list2):
img.paste(pic,(x+i*w,y))
img.paste(im_list2[0],(x+4*w,y))
return img
主函数代码:
h = 300
w = int(300*1.426)
empty_img1 = Image.new("RGBA",(int(4.5*w),int(2.5*h)),'black')
empty_img2 = Image.new("RGBA",(int(4.5*w),int(2.5*h)),'black')
file1 = input('Please input the file names,pic1:')
file2 = input('Please input the file names,pic2:')
file3 = input('Please input the file names,pic3:')
file4 = input('Please input the file names,pic4:')
pic_paste(empty_img1,file1,(h,w),(0,0))
pic_paste(empty_img1,file1,(h,w),(0,2*h))
pic_paste(empty_img1,file2,(h,w),(0,h))
pic_paste(empty_img2,file3,(h,w),(-w//2,-h//2))
pic_paste(empty_img2,file3,(h,w),(-w//2,h+h//2))
pic_paste(empty_img2,file4,(h,w),(-w//2,h//2))
img1 = pil_to_ski(empty_img1,'01.png')
img2 = pil_to_ski(empty_img2,'02.png')
io.imsave('output.png',img1+img2)
input('输出完毕!')
程序制卡效果

designed by python
- 小结 -
△ 方法1 Photoshop 填充模板图
△ 方法2 Python 运行代码
理论
是数学探究必不可少的部分,本篇只做铺垫
代码用了菱块对角线比例,有一定测量误差
理论探究正好可以求出所需精确数据
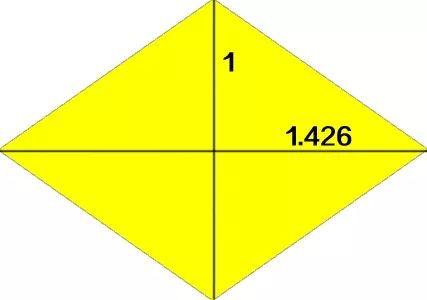
翻转八连粽的菱块对角线
菱块的比例需精确计算,否则有下边两种情况

菱块过高,
无法翻转

菱块过长,中间有空隙
近期学业忙碌,理论下次细说
感兴趣的点击下边
好看
,
1000+点赞拟稿下篇

三阶菱块

四阶菱块
(类似地,可设计 n 阶菱块)

平面六边形

立体八边形















