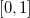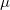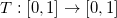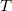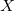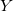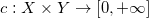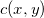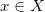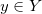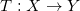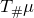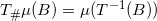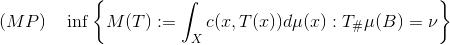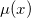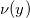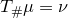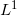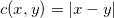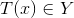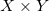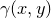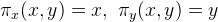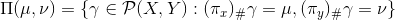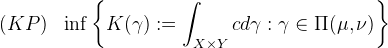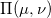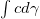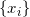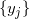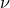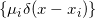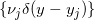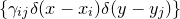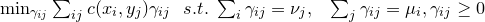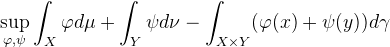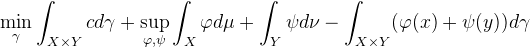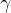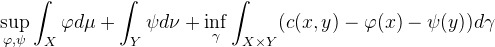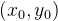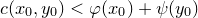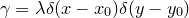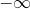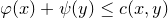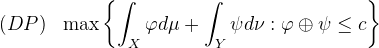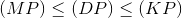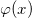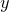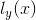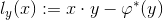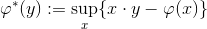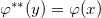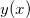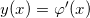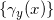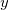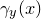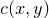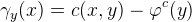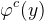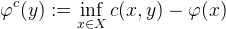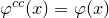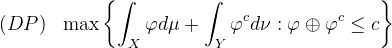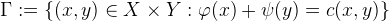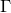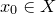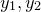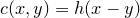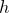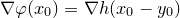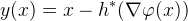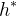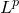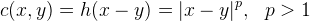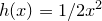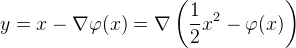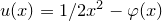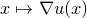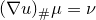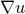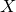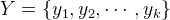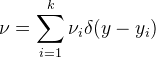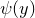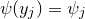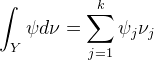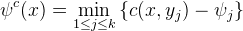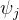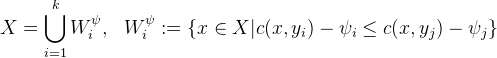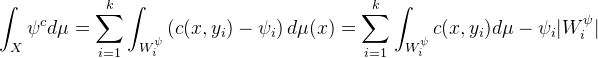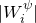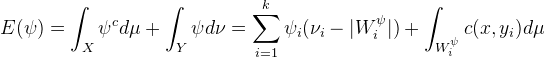![]()
依随智能手机的大规模普及,数字摄影已经成为很多人生活中不可或缺的习惯。随着数字图像处理技术的蓬勃发展,PS作为数字图像处理的代名词(photoshop),在普罗大众中早已耳熟能详。数字图像处理中,最为基本的算法非“色彩变换”(Color Transfer)莫属。
![]()
图1. 直方图均衡化结果(histogram equalization)。
直方图均衡化是提高灰度图像对比度的常见算法。如图1所示,左侧输入图像的灰度分布在一个狭窄区域,朦胧昏暗;右侧是直方图均衡化的结果,清晰明亮,对比鲜明。我们设输入图像像素的灰度为一随机变量,其取值范围为单位区间
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,其概率测度为
,其概率测度为
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,直方图均衡化算法的核心就是求灰度空间(单位区间)到自身的一个映射
,直方图均衡化算法的核心就是求灰度空间(单位区间)到自身的一个映射
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,这一映射将
,这一映射将
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 变换成均匀分布。
变换成均匀分布。
![]()
图2. 基于最优传输的色彩变换。
数据驱动的色彩变换可以视作是直方图均衡化的直接推广。图2显示了一个算例,左侧是输入图像,阴霾遍布下的麦地,阴郁苍凉,中间是范例图像,晴空下的麦穗,右图是输出图像,一扫阴霾,麦浪金黄,明媚爽朗。我们将图像中的每个像素颜色表示成(红,绿,蓝)三元组,所有可能的颜色空间
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 表示成单位立方体,像素为矢量值的随机变量,取值于颜色空间。输入图像的颜色分布的概率测度为
表示成单位立方体,像素为矢量值的随机变量,取值于颜色空间。输入图像的颜色分布的概率测度为
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,范例图像的颜色分布的概率测度为
,范例图像的颜色分布的概率测度为
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 。我们寻找颜色空间的自映射
。我们寻找颜色空间的自映射
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,将概率测度
,将概率测度
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 映成概率测度
映成概率测度
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 。
。
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 将输入图像每个像素的颜色进行变换,从而生成输出图像。
将输入图像每个像素的颜色进行变换,从而生成输出图像。
![]()
图3. 输入图像。
![]()
图4. 范例图像。
![]()
图5. 输出图像。
图3至图5展示了另外一个例子,输入图像颜色的概率测度变换成范例图像颜色的概率测度,从而生成了输出图像。图6的鹦鹉图像也进行了颜色变换。
![]()
图6. 输入的鹦鹉图像。
![]()
图7. 示例图像。
![]()
图8. 输出图像。
这些颜色变换的算法是基于最优传输理论(Optimal Mass Transportation)。最近,最优传输理论被广泛应用于工程和医疗中的诸多领域,例如直接应用于图像颜色变换、图像注册、曲面保面积参数化和体的保体元参数化、曲面或体的注册。特别是在机器学习中,最优传输理论起到了至关重要的作用。下面我们简单介绍最优传输理论梗概。
假设
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 和
和
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 是完备,可分的度量空间,
是完备,可分的度量空间,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 和
和
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 是分别定义在
是分别定义在
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 和
和
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 空间上的概率测度。传输代价函数
空间上的概率测度。传输代价函数
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 为光滑函数,
为光滑函数,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 代表从点
代表从点
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 传输单位质量到点
传输单位质量到点
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 所花费的代价。令
所花费的代价。令
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 为从空间
为从空间
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 到空间
到空间
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 的映射,
的映射,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 将
将
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 推前为
推前为
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 空间上的概率测度
空间上的概率测度
![]() ,其定义如下:令
,其定义如下:令
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 为任意的波莱尔集,则
为任意的波莱尔集,则
![]() 。
。
历史上,法国数学家蒙日(Monge)早在1781年就提出了最优传输问题,我们在这里称之为
蒙日问题
:求保测度的具有最小传输代价的映射
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,
,
![]() 。
。
这一问题的提法非常具有普适性,特别是它具有天然的经济学意义。
我们可以用下面的例子来理解最优传输问题的提法:假设空间
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 和
和
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 都是美国的疆域,
都是美国的疆域,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 是某一年马铃薯的亩产率,在点
是某一年马铃薯的亩产率,在点
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,
,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 是当年每英亩出产马铃薯的吨数;
是当年每英亩出产马铃薯的吨数;
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 是当年马铃薯的每英亩消耗率,在点
是当年马铃薯的每英亩消耗率,在点
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,
,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 是当年每英亩消耗掉的马铃薯的吨数。美国政府需要制定一个马铃薯传输方案,
是当年每英亩消耗掉的马铃薯的吨数。美国政府需要制定一个马铃薯传输方案,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,将马铃薯从生产地点运输到消费地点,使得全国达到供需平衡,即
,将马铃薯从生产地点运输到消费地点,使得全国达到供需平衡,即
![]()
,同时使得总的传输代价最小。这恰恰就是最有传输问题。
蒙日提出的传输代价是
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 距离,
距离,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,数学分析相对困难。因此最优传输问题的理论发展一直停滞不前,岁月蹉跎了一百五十多年,直至1940年代。
,数学分析相对困难。因此最优传输问题的理论发展一直停滞不前,岁月蹉跎了一百五十多年,直至1940年代。
蒙日的提法中,保测度的映射所构成的空间不具备紧性,这为问题的解决带来了本质的难度。1939年,俄罗斯数学家康塔洛维奇(Kantorovich)将传输映射(transportation map)推广为传输方案(transportation plan),从而巧妙地将问题转化,带来实质性的突破。
在蒙日的传输映射
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 中,任意一点
中,任意一点
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 处生产的所有马铃薯,只能运送到唯一的像点
处生产的所有马铃薯,只能运送到唯一的像点
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 。但是在实际生活中,一点处生产的马铃薯可以运送到多个像点,甚至是多个区域,这就是所谓的传输方案。换句话说,传输映射每点的像是一个点,传输方案每点的像是一个集合。
。但是在实际生活中,一点处生产的马铃薯可以运送到多个像点,甚至是多个区域,这就是所谓的传输方案。换句话说,传输映射每点的像是一个点,传输方案每点的像是一个集合。
为了表达传输方案,康塔洛维奇在空间
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 上定义了一个概率测度
上定义了一个概率测度
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,
,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 代表点
代表点
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 处生产的马铃薯有多少运送到了点
处生产的马铃薯有多少运送到了点
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 。那么显然,
。那么显然,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 处所生产的所有马铃薯为
处所生产的所有马铃薯为
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,点
,点
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 处所收到的所有马铃薯为
处所收到的所有马铃薯为
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 。我们定义投影映射如下:
。我们定义投影映射如下:
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,
,
那么如上边际概率条件可以表示为:
![]() 。
。
康塔洛维奇关于最优传输问题的提法如下:
![]() 。
。
我们可以看到可容许概率测度
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 的泛函空间
的泛函空间
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 是一个凸集合,关于
是一个凸集合,关于
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 的能量泛函
的能量泛函
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 是一个线性泛函,紧凸集合上的线性函数达到最大和最小值,如此,康塔洛维奇的最优传输方案的存在性得以保证。
是一个线性泛函,紧凸集合上的线性函数达到最大和最小值,如此,康塔洛维奇的最优传输方案的存在性得以保证。
康塔洛维奇将空间
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 和
和
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 表示成离散点集,
表示成离散点集,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 和
和
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ;将概率测度
;将概率测度
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 和
和
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 离散成狄拉克测度,
离散成狄拉克测度,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 和
和
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ; 同时将传输方案
; 同时将传输方案
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 离散成狄拉克测度
离散成狄拉克测度
![]() 。这样,最优传输方案问题就被转换成经典的线性规划问题,
。这样,最优传输方案问题就被转换成经典的线性规划问题,
![]()
虽然理论上线性规划问题的复杂度为NP,实际中,我们可以用经典的单纯形法或者内点法快速解出。
鉴于最优传输问题的巨大经济价值,康塔洛维奇获得了1975年度的诺贝尔经济学奖。
康塔洛维奇的提法将最优传输问题转化成凸限制下的线性优化问题,这个问题存在对偶的提法。我们可以从对偶问题上看出更多的几何直觉。我们将边际概率测度的限制条件换种方式表达,考察下面的泛函:
![]()
这里
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 是有界连续函数。显然,联合概率分布
是有界连续函数。显然,联合概率分布
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,则泛函值为0;否则,泛函值为
,则泛函值为0;否则,泛函值为
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 。由此,康塔洛维奇问题可以等价表述为:
。由此,康塔洛维奇问题可以等价表述为:
![]()
注意,在这里测度
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 没有任何限制,其在总空间上的积分也可以不等于1。
没有任何限制,其在总空间上的积分也可以不等于1。
在特定条件下,我们可以交换极小,极大算子,从而得到:
![]()
我们再考察后一项
![]()
如果在某一点
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 处,成立严格的不等式:
处,成立严格的不等式:
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,我们取
,我们取
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,则上式趋于
,则上式趋于
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 。反之,如果
。反之,如果
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,并且在某点
,并且在某点
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 处等号成立,则上式为0。由此,我们可以得到对偶问题的提法:
处等号成立,则上式为0。由此,我们可以得到对偶问题的提法:
![]() ,
,
这里
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 是有界连续函数。
是有界连续函数。
通常情况下,蒙日泛函,对偶泛函和康塔洛维奇泛函满足不等式,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,
,
问题的核心在于:何时等号成立?何时最优传输方案称为最优传输映射?
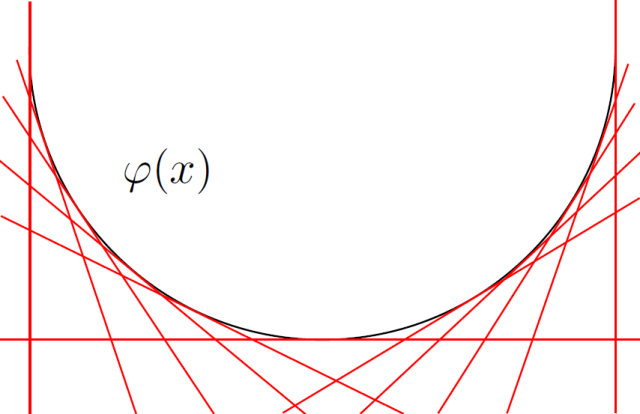
对偶问题具有非常直观的几何洞察,为此我们先考察凸几何中的勒让德变换(Legendre transform)。
![]()
图9. 勒让德变换。
如图9所示,假设
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 是一个凸函数,亦即其图为一凸曲线。则
是一个凸函数,亦即其图为一凸曲线。则
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 的图,是其所有切线的包络(envelope)。斜率为
的图,是其所有切线的包络(envelope)。斜率为
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 的切线记为
的切线记为
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,方程表示为
,方程表示为
![]() ,
,
这里截距定义为:
![]()
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 就是
就是
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 的勒让德变换,它们互为勒让德共轭,换言之,
的勒让德变换,它们互为勒让德共轭,换言之,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 。几何上,
。几何上,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 的勒让德变换给出了
的勒让德变换给出了
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 的所有切线,这些切线的包络给出了
的所有切线,这些切线的包络给出了
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 。每一个
。每一个
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 对应着唯一的
对应着唯一的
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,这里
,这里
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 。
。
![]()
图10. c-变换。
我们可以将勒让德变换进行推广,如图10所示,假设
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 是单参数曲线族,以变元
是单参数曲线族,以变元
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 为参数,曲线族的包络为
为参数,曲线族的包络为
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 。这里,曲线
。这里,曲线
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 由传输代价函数
由传输代价函数
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 所决定,其方程表示为:
所决定,其方程表示为:
![]()
这里,我们称
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 为
为
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 的c-变换(c-transform),
的c-变换(c-transform),
![]() 。
。
如果
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,则我们说
,则我们说
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 为c-凸函数(c-convex)。
为c-凸函数(c-convex)。
对偶问题(DP)可以进一步表示成如下形式:
![]() 。
。
根据以上的讨论,我们看到对于最优传输方案
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,其质量主要集中于集合
,其质量主要集中于集合
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,
,
换言之
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 。如果
。如果
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 是n维流形,对于任意
是n维流形,对于任意
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,
,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 由
由
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 唯一决定,则最优传输方案
唯一决定,则最优传输方案
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 成为最优传输映射。
成为最优传输映射。
根据包络的几何特征,假设在
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 处,
处,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 和
和
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 相切,我们得到必要条件:
相切,我们得到必要条件:
![]() ,
,
![]()
图11. 扭曲条件。
我们得到映射 ,如果这一映射对任意
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 都是单射,则我们说代价函数
都是单射,则我们说代价函数
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 满足扭曲条件(twist condition)。可以看出,如果代价函数
满足扭曲条件(twist condition)。可以看出,如果代价函数
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 满足扭曲条件,则对于任意的
满足扭曲条件,则对于任意的
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,满足相切条件的
,满足相切条件的
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 唯一,因此映射
唯一,因此映射
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 就是最优传输映射。
就是最优传输映射。
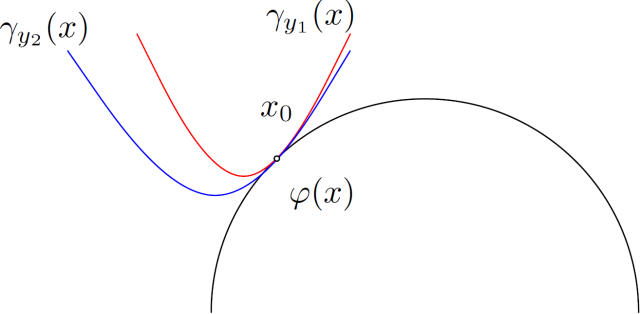
图11展示了一个不满足扭曲条件的例子,在
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 处,存在
处,存在
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 同时满足相切条件。
同时满足相切条件。
假如,代价函数
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,这里
,这里
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 是一个严格的凸函数,那么它满足扭曲条件,
是一个严格的凸函数,那么它满足扭曲条件,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,则传输映射有表达式:
,则传输映射有表达式:
![]()
这里,我们再一次用到了勒让德变换
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 。
。
作为这套理论的应用,我们给出两个在日常生活中最为常见的例子。
考察代价函数为
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 距离,
距离,
![]()
则h为严格凸的函数,最优传输映射存在。如果我们考虑
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 距离情形,
距离情形,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,则其勒让德变换为恒同变换,最优传输映射公式为:
,则其勒让德变换为恒同变换,最优传输映射公式为:
![]()
我们令
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,则得到所谓的Brenier定理:
,则得到所谓的Brenier定理:
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 距离的最优传输映射由一个函数的梯度
距离的最优传输映射由一个函数的梯度
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 给出。
给出。
我们再考虑保持测度的性质:
![]() ,我们就会得到著名的蒙日-安培方程。梯度映射
,我们就会得到著名的蒙日-安培方程。梯度映射
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 的雅克比行列式为海森矩阵,
的雅克比行列式为海森矩阵,
![]()
因此,最优传输映射和蒙日-安培方程具有非常亲密的血缘关系,而后者也和传统的闵科夫斯基问题(Minkowski Problem)有很深的渊源
[5]
。
从计算角度讲,最优传输映射和计算几何中的加权Voronoi图(Power Voronoi Diagram)是彼此等价的。我们在这里进行一番推导。
我们设
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 是欧式空间中的紧凸集,
是欧式空间中的紧凸集,
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 为离散点集,
为离散点集,
![]() ,
,
配备狄拉克测度:
![]() 。
。
考察对偶问题,则
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 为离散函数,定义在离散点集上,设
为离散函数,定义在离散点集上,设
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,则
,则
![]() ,
,
我们在考察
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 的c-变换,得到
的c-变换,得到
![]() ,
,
固定
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() ,函数
,函数
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 关于
关于
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 为凹函数。由此,我们得到Power Voronoi图,
为凹函数。由此,我们得到Power Voronoi图,
![]()
我们得到
![]()
这里
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() 是相应的Voronoi胞腔的
是相应的Voronoi胞腔的
![This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.]() -体积。
-体积。
由此,我们得到对偶问题为:最大化如下能量
![]()
这一能量为凹函数,其梯度为
![]()
我们可以用爬山法来进行优化。图12,13显示了保面元和保体元的同胚映射,其计算就是基于这个算法。更多的计算工具,数据测试集合可以在
[2]
中找到。
![]()
图12. 曲面保面积参数化
[4]
。
![]()
![]()
图13. 保体元的参数化
[3]
。
一个黎曼流形上的所有概率测度构成一个无穷维的流形,即所谓的Wasserstein空间。任意两个概率测度之间存在最优传输映射,这个映射的传输代价给出了两个概率测度之间的距离,被称为是Wasserstein距离。因此,Wasserstein空间是一个黎曼流形。
在工程和医学的诸多领域,算法的核心是寻找一个概率测度,例如机器学习算法。Wasserstein距离给出了衡量概率测度相似程度的严密方法,这是为什么近几年来最优传输理论异常火热的根本原因。
但是,计算最优传输本身并不容易,目前计算机视觉、图形学、机器学习、医学图像的研究者都努力用各种优化方法,工程技巧来提高计算效率。我们可以预见在不久的将来,最优传输理论将会在更多的实际工程中大放异彩。
(丘成桐先生邀请杜克大学的刘建国教授在清华大学数学科学中心,于2016年暑期学校,讲述最优传输理论课程
[1]
。本文根据课堂笔记整理而成。笔者鸣谢丘成桐先生和刘建国教授。)
[1] Fillipo Santambrogio, Optimal Transport for Applied Mathematicians - Calculus of Variations, PDEs and Modeling
[2] http://www3.cs.stonybrook.edu/~gu/software/omt/index.html
[3] Kehua Su, Wei Chen, Na Lei, Junwei Zhang, Kun Qian and Xianfeng Gu, Volume Preserving Mesh Parameterization based on Optimal Mass Transportation, Journal of Computer-Aided Design (CAD), 2016.
[4] Xin Zhao, Zhengyu Su, Xianfeng David Gu, Arie Kaufman, Jian Sun, Jie Gao, Feng Luo, Area-preservation Mapping using Optimal Mass Transport, IEEE TVCG, 19(12), Pages 2838-2847, 2013.
[5] Xianfeng Gu, Feng Luo, Jian Sun and Shing-Tung Yau, Variational Principles forMinkowski Type Problems, Discrete Optimal Transport, and Discrete Monge-Ampere
Equations, Vol. 20, No. 2, pp. 383-398, Asian Journal of Mathematics (AJM), April 2016.
投稿、授权等请联系:
[email protected]
您可回复"年份+月份"(如201510),
获取指定年月文章,
或返回主页点击子菜单获取或搜索往期文章。
赛先生
由百人传媒投资和创办,
文小刚、刘克峰、颜宁
三位国际著名科学家担任主编,告诉你正在发生的科学。
上帝忘了给我们翅膀,于是,科学家带领我们飞翔。
微信号:
iscientists
![]()
▲
长按图片识别二维码关注我们