SLAM 后端的优化方式大体分为滤波和优化。近些年优化越来越成为主流,在学习优化之前,掌握滤波的工作原理也十分必要。
一、引言
滤波问题可以简单理解为“预测 +观测 =融合结果”。
结合实际点云地图中定位的例子,预测由IMU给出,观测即为激光雷达点云和地图匹配得到的姿态和位置。
融合流程用框图可以表示如下
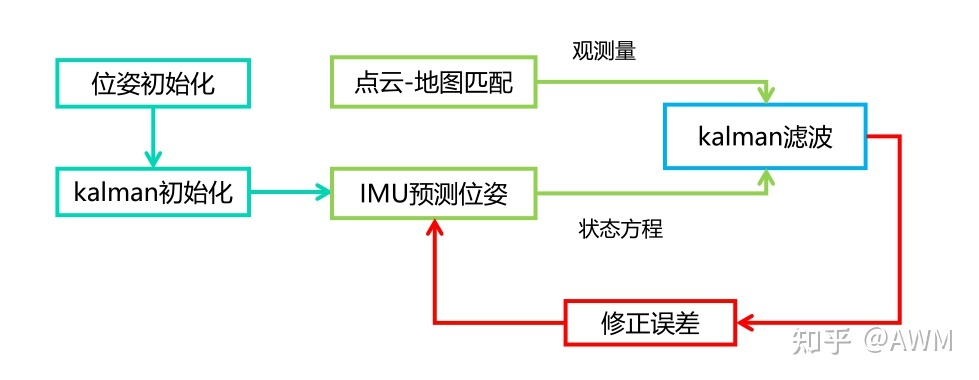
简述kalman滤波:
为了避免复杂的公式推导,大多数只给出结论:
贝叶斯滤波
贝叶斯滤波的信息流图如下:
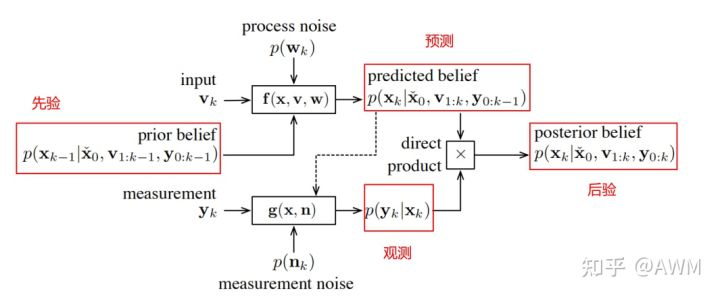
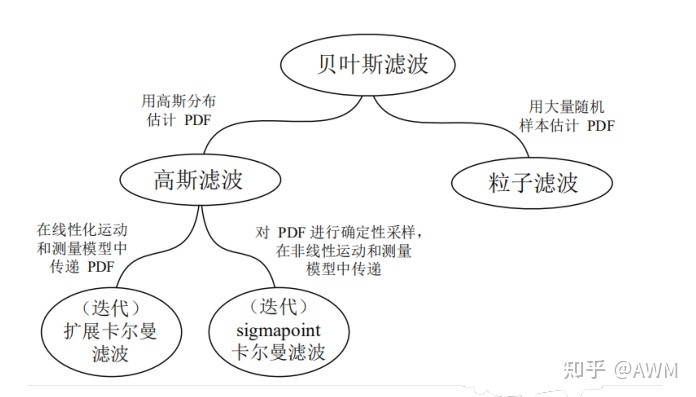
在高斯假设前提下,用贝叶斯滤波的原始形式推导比较复杂,可以利用高斯的特征得到简化形式,即广义高斯滤波。后面KF、EKF、IEKF的推导均采用这种形式。
卡尔曼滤波(KF)推导


二、基于滤波的融合
1.状态方程

2.观测方程

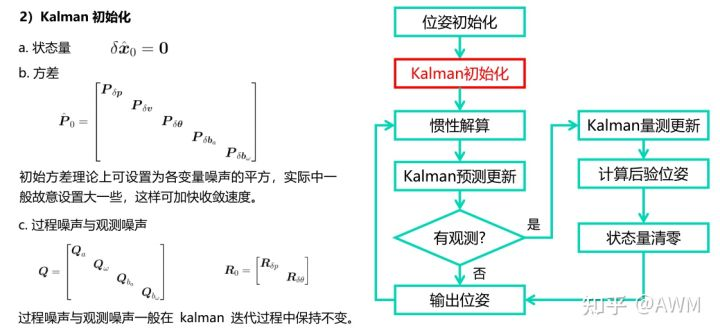
3.构建滤波器

4.Kalman滤波实际使用流程
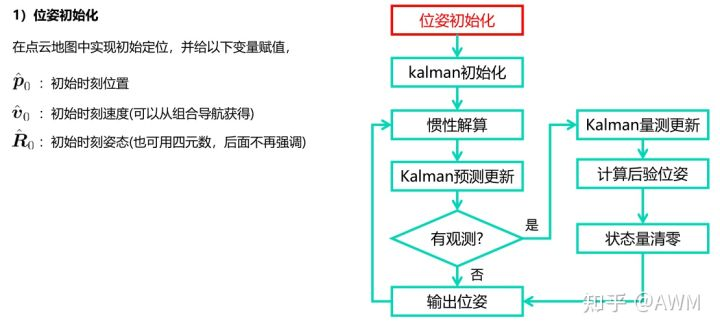
代码:
/**
* @brief init filter
* @param pose, init pose
* @param vel, init vel
* @param imu_data, init IMU measurements
* @return true if success false otherwise
*/
void ErrorStateKalmanFilter::Init(const Eigen::Vector3d &vel,
const IMUData &imu_data) {
// init odometry:
Eigen::Matrix3d C_nb = imu_data.GetOrientationMatrix().cast();
// a. init C_nb using IMU estimation:
pose_.block<3, 3>(0, 0) = C_nb;
// b. convert flu velocity into navigation frame:
vel_ = C_nb * vel;
// save init pose:
init_pose_ = pose_;
// init IMU data buffer:
imu_data_buff_.clear();
imu_data_buff_.push_back(imu_data);
// init filter time:
time_ = imu_data.time;
// set process equation in case of one step prediction & correction:
Eigen::Vector3d linear_acc_init(imu_data.linear_acceleration.x,
imu_data.linear_acceleration.y,
imu_data.linear_acceleration.z);
Eigen::Vector3d angular_vel_init(imu_data.angular_velocity.x,
imu_data.angular_velocity.y,
imu_data.angular_velocity.z);
// covert to navigation frame:
linear_acc_init = linear_acc_init - accl_bias_; // body 系下
angular_vel_init = GetUnbiasedAngularVel(angular_vel_init, C_nb);
// init process equation, in
case of direct correct step:
UpdateProcessEquation(linear_acc_init, angular_vel_init);
LOG(INFO) < <"Kalman Filter Inited at " <(time_)
< <"Init Position: " <", " <", "
< <"Init Velocity: " <", " <", "
<}
// 设置状态方程
void ErrorStateKalmanFilter::UpdateProcessEquation(
const Eigen::Vector3d &linear_acc_mid,
const Eigen::Vector3d &angular_vel_mid) {
// set linearization point:
Eigen::Matrix3d C_nb = pose_.block<3, 3>(0, 0); // n2b 转换矩阵
Eigen::Vector3d f_b = linear_acc_mid + g_; // 加速度
Eigen::Vector3d w_b = angular_vel_mid; // 角速度
// set process equation:
SetProcessEquation(C_nb, f_b, w_b);
}
/**
* @brief set process equation
* @param C_nb, rotation matrix, body frame -> navigation frame
* @param f_n, accel measurement in navigation frame
* @return void
*/
void ErrorStateKalmanFilter::SetProcessEquation(const Eigen::Matrix3d &C_nb, // 更新状态方程 F矩阵
const Eigen::Vector3d &f_b,
const Eigen::Vector3d &w_b) {
// TODO: set process / system equation:
// a. set process equation for delta vel:
F_.setZero();
F_.block<3, 3>(kIndexErrorPos, kIndexErrorVel) = Eigen::Matrix3d::Identity();
F_.block<3, 3>(kIndexErrorVel, kIndexErrorOri) = - C_nb * Sophus::SO3d::hat(f_b).matrix();
F_.block<3, 3>(kIndexErrorVel, kIndexErrorAccel) = -C_nb;
F_.block<3, 3>(kIndexErrorOri, kIndexErrorOri) = - Sophus::SO3d::hat(w_b).matrix();
F_.block<3, 3>(kIndexErrorOri, kIndexErrorGyro) = - Eigen::Matrix3d::Identity();
// b. set process equation for delta ori:
B_.setZero();
B_.block<3, 3>(kIndexErrorVel, kIndexNoiseGyro) = C_nb;
B_.block<3, 3>(kIndexErrorOri, kIndexNoiseGyro) = Eigen::Matrix3d::Identity();
if(COV.PROCESS.BIAS_FLAG){ // 判断是否考虑随机游走
B_.block<3, 3>(kIndexErrorAccel, kIndexNoiseBiasAccel) = Eigen::Matrix3d::Identity();
B_.block<3, 3>(kIndexErrorGyro, kIndexNoiseBiasGyro) = Eigen::Matrix3d::Identity();
}
}
// c. process noise:
Q_.block<3, 3>(kIndexNoiseAccel, kIndexNoiseAccel) = COV.PROCESS.ACCEL * Eigen::Matrix3d::Identity();
Q_.block<3, 3>(kIndexNoiseGyro, kIndexNoiseGyro) = COV.PROCESS.GYRO * Eigen::Matrix3d::Identity();
if (COV.PROCESS.BIAS_FLAG ){
Q_.block<3, 3>(kIndexNoiseBiasAccel, kIndexNoiseBiasAccel) = COV.PROCESS.BIAS_ACCEL * Eigen::Matrix3d::Identity();
Q_.block<3, 3>(kIndexNoiseBiasGyro, kIndexNoiseBiasGyro) = COV.PROCESS.BIAS_GYRO * Eigen::Matrix3d::Identity();
}
// d. measurement noise:
RPose_.block<3, 3>(0, 0) = COV.MEASUREMENT.POSE.POSI * Eigen::Matrix3d::Identity();
RPose_.block<3, 3>(3, 3) = COV.MEASUREMENT.POSE.ORI * Eigen::Matrix3d::Identity();
// e. process equation:
F_.block<3, 3>(kIndexErrorPos, kIndexErrorVel) = Eigen::Matrix3d::Identity();
F_.block<3, 3>(kIndexErrorOri, kIndexErrorGyro) = -Eigen::Matrix3d::Identity();
B_.block<3, 3>(kIndexErrorOri, kIndexNoiseGyro) = Eigen::Matrix3d::Identity();
B_.block<3, 3>(kIndexErrorAccel, kIndexNoiseBiasAccel) = Eigen::Matrix3d::Identity();
B_.block<3, 3>(kIndexErrorGyro, kIndexNoiseBiasGyro) = Eigen::Matrix3d::Identity();
// f. measurement equation:
GPose_.block<3, 3>(0, kIndexErrorPos) = Eigen::Matrix3d::Identity();
GPose_.block<3, 3>(3, kIndexErrorOri) = Eigen::Matrix3d::Identity();
CPose_.block<3, 3>(0, 0) = Eigen::Matrix3d::Identity();
CPose_.block<3, 3>(3, 3) = Eigen::Matrix3d::Identity();
// init soms:
QPose_.block(0, 0) = GPose_;
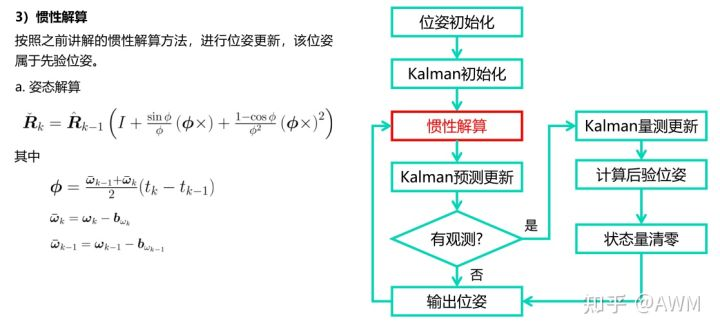
这部分是惯导解算的内容,在Updata()函数中:
在Updata()函数中有两个重要的函数,即UpdateOdomEstimation
()
,UpdateErrorEstimation
()
,分别做名义值更新和误差值更新
bool ErrorStateKalmanFilter::Update(const IMUData &imu_data) {
//
// TODO: understand ESKF update workflow
//
// update IMU buff:
if (time_ // update IMU odometry:
Eigen::Vector3d linear_acc_mid;
Eigen::Vector3d angular_vel_mid;
imu_data_buff_.push_back(imu_data);
UpdateOdomEstimation(linear_acc_mid, angular_vel_mid); // 做名义值更新
imu_data_buff_.pop_front();
// update error estimation:
double T = imu_data.time - time_;
UpdateErrorEstimation(T, linear_acc_mid, angular_vel_mid); // 做误差值更新
// move forward:
time_ = imu_data.time;
return true;
}
return false;
}
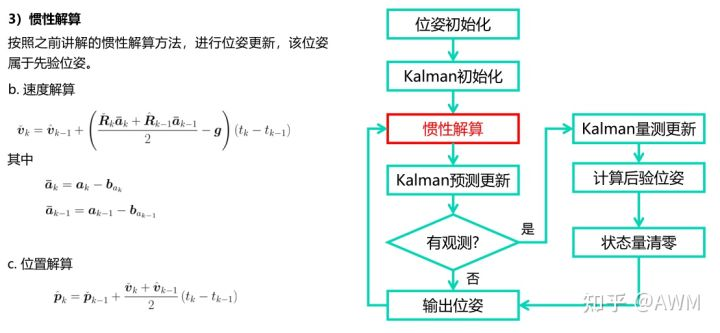
名义值状态量(位置、速度、姿态、陀螺仪bias、加计bias)更新函数:UpdateOdomEstimation(linear_acc_mid, angular_vel_mid):
void ErrorStateKalmanFilter::UpdateOdomEstimation( // 更新名义值
Eigen::Vector3d &linear_acc_mid, Eigen::Vector3d &angular_vel_mid) {
//
// TODO: this is one possible solution to previous chapter, IMU Navigation,
// assignment
//
// get deltas:
size_t index_curr_ = 1;
size_t index_prev_ = 0;
Eigen::Vector3d angular_delta = Eigen::Vector3d::Zero();
GetAngularDelta(index_curr_, index_prev_, angular_delta, angular_vel_mid); // 获取等效旋转矢量, 保存角速度中值
// update orientation:
Eigen::Matrix3d R_curr_ = Eigen::Matrix3d::Identity();
Eigen::Matrix3d R_prev_ = Eigen::Matrix3d::Identity();
UpdateOrientation(angular_delta, R_curr_, R_prev_); // 更新四元数
// get velocity delta:
double delta_t_;
Eigen::Vector3d velocity_delta_;
GetVelocityDelta(index_curr_, index_prev_, R_curr_, R_prev_, delta_t_, velocity_delta_, linear_acc_mid); // 获取速度差值, 保存线加速度中值
// save mid-value unbiased linear acc for error-state update:
// update position:
UpdatePosition(delta_t_, velocity_delta_);
}
惯导解算中,分别对应

//旋转向量解算:
bool ErrorStateKalmanFilter::GetAngularDelta(const size_t index_curr,
const size_t index_prev,
Eigen::Vector3d &angular_delta,
Eigen::Vector3d &angular_vel_mid) {
if (index_curr <= index_prev || imu_data_buff_.size() <= index_curr) {
return false;
}
const IMUData &imu_data_curr = imu_data_buff_.at(index_curr);
const IMUData &imu_data_prev = imu_data_buff_.at(index_prev);
double delta_t = imu_data_curr.time - imu_data_prev.time;
Eigen::Vector3d angular_vel_curr = Eigen::Vector3d(
imu_data_curr.angular_velocity.x, imu_data_curr.angular_velocity.y,
imu_data_curr.angular_velocity.z);
Eigen::Matrix3d R_curr = imu_data_curr.GetOrientationMatrix().cast();
angular_vel_curr = GetUnbiasedAngularVel(angular_vel_curr, R_curr);
Eigen::Vector3d angular_vel_prev = Eigen::Vector3d(
imu_data_prev.angular_velocity.x, imu_data_prev.angular_velocity.y,
imu_data_prev.angular_velocity.z);
Eigen::Matrix3d R_prev = imu_data_prev.GetOrientationMatrix().cast();
angular_vel_prev = GetUnbiasedAngularVel(angular_vel_prev, R_prev);
angular_delta = 0.5 * delta_t * (angular_vel_curr + angular_vel_prev);
angular_vel_mid = 0.5 * (angular_vel_curr + angular_vel_prev);
return true;
}
// 姿态解算
void ErrorStateKalmanFilter::UpdateOrientation(
const Eigen::Vector3d &angular_delta, Eigen::Matrix3d &R_curr,
Eigen::Matrix3d &R_prev) {
// magnitude:
double angular_delta_mag = angular_delta.norm();
// direction:
Eigen::Vector3d angular_delta_dir = angular_delta.normalized();
// build delta q:
double angular_delta_cos = cos(angular_delta_mag / 2.0);
double angular_delta_sin = sin(angular_delta_mag / 2.0);
Eigen::Quaterniond dq(angular_delta_cos,
angular_delta_sin * angular_delta_dir.x(),
angular_delta_sin * angular_delta_dir.y(),
angular_delta_sin * angular_delta_dir.z());
Eigen::Quaterniond q(pose_.block<3, 3>(0, 0));
// update:
q = q * dq;
// write back:
R_prev = pose_.block<3, 3>(0, 0);
pose_.block<3, 3>(0, 0) = q.normalized().toRotationMatrix();
R_curr = pose_.block<3, 3>(0, 0);
}
//速度解算
bool ErrorStateKalmanFilter::GetVelocityDelta(
const size_t index_curr, const size_t index_prev,
const Eigen::Matrix3d &R_curr, const Eigen::Matrix3d &R_prev, double &T,
Eigen::Vector3d &velocity_delta, Eigen::Vector3d &linear_acc_mid) {
if (index_curr <= index_prev || imu_data_buff_.size() <= index_curr) {
return false;
}
const IMUData &imu_data_curr = imu_data_buff_.at(index_curr);
const IMUData &imu_data_prev = imu_data_buff_.at(index_prev);
T = imu_data_curr.time - imu_data_prev.time;
Eigen::Vector3d linear_acc_curr = Eigen::Vector3d(
imu_data_curr.linear_acceleration.x, imu_data_curr.linear_acceleration.y,
imu_data_curr.linear_acceleration.z);
Eigen::Vector3d a_curr = GetUnbiasedLinearAcc(linear_acc_curr, R_curr); // w系下的a_curr
Eigen::Vector3d linear_acc_prev = Eigen::Vector3d(
imu_data_prev.linear_acceleration.x, imu_data_prev.linear_acceleration.y,
imu_data_prev.linear_acceleration.z);
Eigen::Vector3d a_prev = GetUnbiasedLinearAcc(linear_acc_prev, R_prev); // w系下的a_prev
// mid-value acc can improve error state prediction accuracy:
linear_acc_mid = 0.5 * (a_curr + a_prev); // w 系下的linear_acc_mid , 用于更新pos_w 和 vel_w
velocity_delta = T * linear_acc_mid;
linear_acc_mid = 0.5 * (linear_acc_curr + linear_acc_prev) - accl_bias_; // b 系下的linear_acc_mid
return true;
}
// 位置解算
void ErrorStateKalmanFilter::UpdatePosition(
const double &T, const Eigen::Vector3d &velocity_delta) {
pose_.block<3, 1>(0, 3) += T * vel_ + 0.5 * T * velocity_delta;
vel_ += velocity_delta;
}
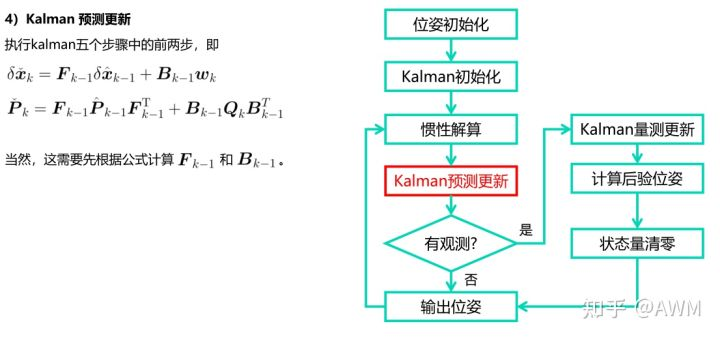
kalman预测更新,误差值更新
void ErrorStateKalmanFilter::UpdateErrorEstimation( // 更新误差值
const double &T, const Eigen::Vector3d &linear_acc_mid,
const Eigen::Vector3d &angular_vel_mid) {
static MatrixF F_1st;
static MatrixF F_2nd;
// TODO: update process equation: // 更新状态方程
UpdateProcessEquation(linear_acc_mid , angular_vel_mid);
// TODO: get discretized process equations: // 非线性化
F_1st = F_ * T; // T kalman 周期
MatrixF F = MatrixF::Identity() + F_1st;
MatrixB B = MatrixB::Zero();
B.block<3, 3>(kIndexErrorVel, kIndexNoiseGyro) = B_.block<3, 3>(kIndexErrorVel, kIndexNoiseGyro) * T;
B.block<3, 3>(kIndexErrorOri, kIndexNoiseGyro) = B_.block<3, 3>(kIndexErrorOri, kIndexNoiseGyro) *T;
if(COV.PROCESS.BIAS_FLAG){
B.block<3, 3>(kIndexErrorAccel, kIndexNoiseBiasAccel) = B_.block<3, 3>(kIndexErrorAccel, kIndexNoiseBiasAccel)* sqrt(T);
B.block<3, 3>(kIndexErrorGyro, kIndexNoiseBiasGyro) = B_.block<3, 3>(kIndexErrorGyro, kIndexNoiseBiasGyro)* sqrt(T);
}
// TODO: perform Kalman prediction
X_ = F * X_;
P_ = F * P_ * F.transpose() + B * Q_ * B.transpose(); // 只有方差进行了计算
}
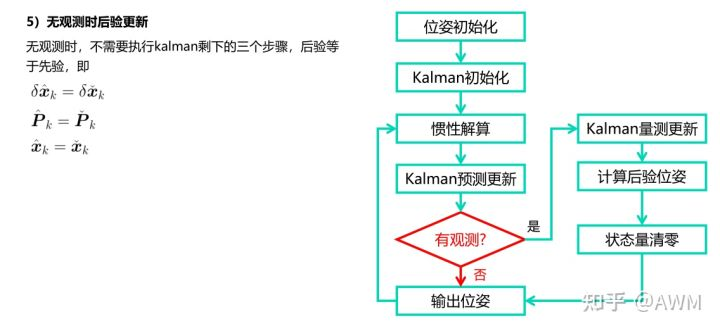
根据是否有观测,来更新后验估计
void ErrorStateKalmanFilter::CorrectErrorEstimation(
const MeasurementType &measurement_type, const Measurement &measurement) {
//
// TODO: understand ESKF correct workflow
//
Eigen::VectorXd Y;
Eigen::MatrixXd G, K;
switch (measurement_type) {
case MeasurementType::POSE:
CorrectErrorEstimationPose(measurement.T_nb, Y, G, K);
break;
default:
break;
}
// TODO: perform Kalman correct:
P_ = (MatrixP::Identity() - K*G) * P_ ; // 后验方差
X_ = X_ + K * (Y - G*X_); // 更新后的状态量
}
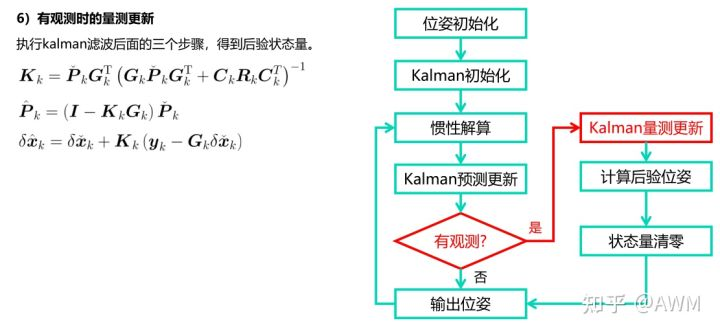
当有观测时:依据下面公式

代码对应
/**
* @brief correct error estimation using pose measurement
* @param T_nb, input pose measurement
* @return void
*/
void ErrorStateKalmanFilter::CorrectErrorEstimationPose( // 计算 Y ,G ,K
const Eigen::Matrix4d &T_nb, Eigen::VectorXd &Y, Eigen::MatrixXd &G,
Eigen::MatrixXd &K) {
//
// TODO: set measurement: 计算观测 delta pos 、 delta ori
//
Eigen::Vector3d dp = pose_.block<3, 1>(0, 3) - T_nb.block<3, 1>(0, 3);
Eigen::Matrix3d dR = T_nb.block<3, 3>(0, 0).transpose() * pose_.block<3, 3>(0, 0) ;
// TODO: set measurement equation:
Eigen::Vector3d dtheta = Sophus::SO3d::vee(dR - Eigen::Matrix3d::Identity() );
YPose_.block<3, 1>(0, 0) = dp; // delta position
YPose_.block<3, 1>(3, 0) = dtheta; // 失准角
Y = YPose_;
// set measurement G
GPose_.setZero();
GPose_.block<3, 3>(0, kIndexErrorPos) = Eigen::Matrix3d::Identity();
GPose_.block<3 ,3>(3, kIndexErrorOri) = Eigen::Matrix3d::Identity();
G = GPose_;
// set measurement C
CPose_.setZero();
CPose_.block<3, 3>(0,kIndexNoiseAccel) = Eigen::Matrix3d::Identity();
CPose_.block<3, 3>(3,kIndexNoiseGyro) = Eigen::Matrix3d::Identity();
Eigen::MatrixXd C = CPose_;
// TODO: set Kalman gain:
Eigen::MatrixXd R = RPose_; // 观测噪声
K = P_ * G.transpose() * ( G * P_ * G.transpose( ) + C * RPose_* C.transpose() ).inverse() ;
}
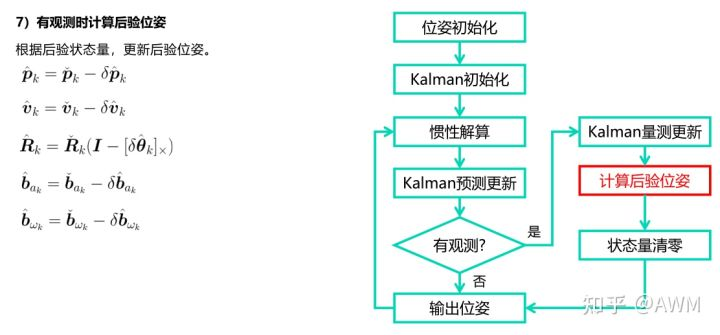
对应代码
void ErrorStateKalmanFilter::EliminateError(void) {
// 误差状态量 X_ : 15*1
// TODO: correct state estimation using the state of ESKF
//
// a. position:
// do it!
pose_.block<3, 1>(0, 3) -= X_.block<3, 1>(kIndexErrorPos, 0 ); // 减去error
// b. velocity:
// do it!
vel_ -= X_.block<3,1>(kIndexErrorVel, 0 );
// c. orientation:
// do it!
Eigen::Matrix3d dtheta_cross = Sophus::SO3d::hat(X_.block<3,1>(kIndexErrorOri, 0)); // 失准角的反对称矩阵
pose_.block<3, 3>(0, 0) = pose_.block<3, 3>(0, 0) * (Eigen::Matrix3d::Identity() - dtheta_cross);
Eigen::Quaterniond q_tmp(pose_.block<3, 3>(0, 0) );
q_tmp.normalize(); // 为了保证旋转矩阵是正定的
pose_.block<3, 3>(0, 0) = q_tmp.toRotationMatrix();
// d. gyro bias:
if (IsCovStable(kIndexErrorGyro)) {
gyro_bias_ -= X_.block<3, 1>(kIndexErrorGyro, 0); // 判断gyro_bias_error是否可观
}
// e. accel bias:
if (IsCovStable(kIndexErrorAccel)) {
accl_bias_ -= X_.block<3, 1>(kIndexErrorAccel, 0); // 判断accel_bias_error是否可观

















