今天的这本书有点不一样,它是一本讲数学思维的书。
文科妈妈们请别怕!
因为,以你们的优势绝对可以hold得住它!

但在读这本书之前,建议你和孩子都先把自己当成古人,然后用学习历史的思路来读这本书!
先开一个好头,然后剩下的可以教给孩子们自主阅读了。当然,这个过程里还是会鼓励家长和孩子们一起讨论,因为里面的知识小趣味,要互动起来才更有意思!
至于怎么讨论,或者有哪些可以讨论的点,大家先不要急,我会在本书的亮点解读部分逐一为你们解释。

推荐理由:
-
一流出版社精心打造
-
层层递进、时间线清晰、训练孩子的纵向思维
-
探究古代文明、横向对比、培养孩子的大局观
-
抽象概念简单化、故事+问答+游戏相互结合趣味多
-
与生活场景密切相连,拉近数学与真实世界的距离
-
梳理人物贡献与专属词汇,方便查找加深理解
这本《DK了不起的数学思维》是DK出版社的做新作品。了解DK的朋友们都知道,DK的书向来以专业的内容、鲜明的视觉设计不断引领着国际图文书的出版风格,并在不同领域出版了多种类别的成人及儿童非虚构类图书。至今,已有60余种语言的出版物畅销于全球超过100个国家,共有千余名员工分布于欧美、澳洲、亚太等地区。

作为史上极成功的图文书出版社之一,DK代表的不仅是一种图文并茂的美学风格,更是一种面对世界和知识的态度。正如DK做书的理念——A World of Ideas:See all there is to know。正是希望用严谨且实用的知识与创意逻辑并存的设计,引发思考、启迪灵感,让读者在阅读中享受探索未知的乐趣。
层层递进、时间线清晰、训练孩子的纵向思维
整本书是围绕五大板块讨论的:“数字与计数有什么用?“、“形状与测量有什么用?”、“规律与数列有什么用?“、“数据与统计有什么用?“、概率与逻辑有什么用?“;而每一个板块下,都会延伸出5-6个小问题。
因此,在这本书里,总共有30个问题。整本书都是用故事与图解相结合的方式进行展开的。而且形式多样、深入浅出、层层递进!通过一个个的小问题,引出无数流传千年的数学趣闻,从而探究数学本源以及数学在实际生活当中的应用。


首先开篇部分“数字与计数有什么用”,主要讲的是数字的起源及各种计数法的发展,这部分就是文科妈妈与孩子进行亲子共读时锻炼孩子进行纵向思维的好时机!
我们知道,没有数字,人类就无法进步。可是,关于数字的秘密,很多人并不了解。
开头我说了,读这本书,建议大家带着孩子一起先把自己想象成原始人。那么作为一个站在知识原点的古人,日复一日,该如何记录每一天的时间及周围事物的数量呢?
“用石头画线条!”当我问儿子同样的问题时,儿子这样回答我。你看,小孩子的想象力其实是很丰富的,虽然他们会的“知识”有限,但他们依旧能够用看似最“笨”、也最简单的方法去了解周围的世界。
事实上,古人计数的历史最早可以追溯到35000年前的非洲!
历史学家认为,我们的祖先在那时候便开始使用刻道(画竖线)的方法记录不同的月相以及经过的天数,这些对狩猎者和采集者的生存至关重要。刻道计数法是一种简单的线条系统,最初形式是用线条的树木代表物体的数目。
早期人类用它来记录数字和数量。每当看到月亮的形状发生变化时,就刻一道新的痕迹,如此反复,日积月累人类便制作出了世界上第一部阴历!

下面这张图就是古人用刻道法记录月相呈现出的周期性变化。你会发现,其实古人也很聪明,因为在“满月”的时候,他们刻出的道明显要比其他线条“长”一些!

虽然画竖线的方式简单快捷,但古人也发现这样的方式有时候并不完美。因为一旦要记录大一点的数字比如100,那么就意味着必须要画上100条线!这样就会非常不方便。因此,人们开始将刻道进行了分组。
如果说1用一条竖线代表,以此类推,那么到5的时候就会变成一条斜线穿过已有的4条竖线;而到6的时候,就在5的旁边加上一条单独的竖线;而在记录10的时候,在第二组的4条刻道上加一条斜线。

而随着时间的推移,还出现了“点线计数法“、以及“正字计数法”。
点线计数法
是利用点与线组合计数的方法。数字1-4用点代表。数字5-10则是在两点之间分别添加线条,先形成一个正方形,然后添加对角线。
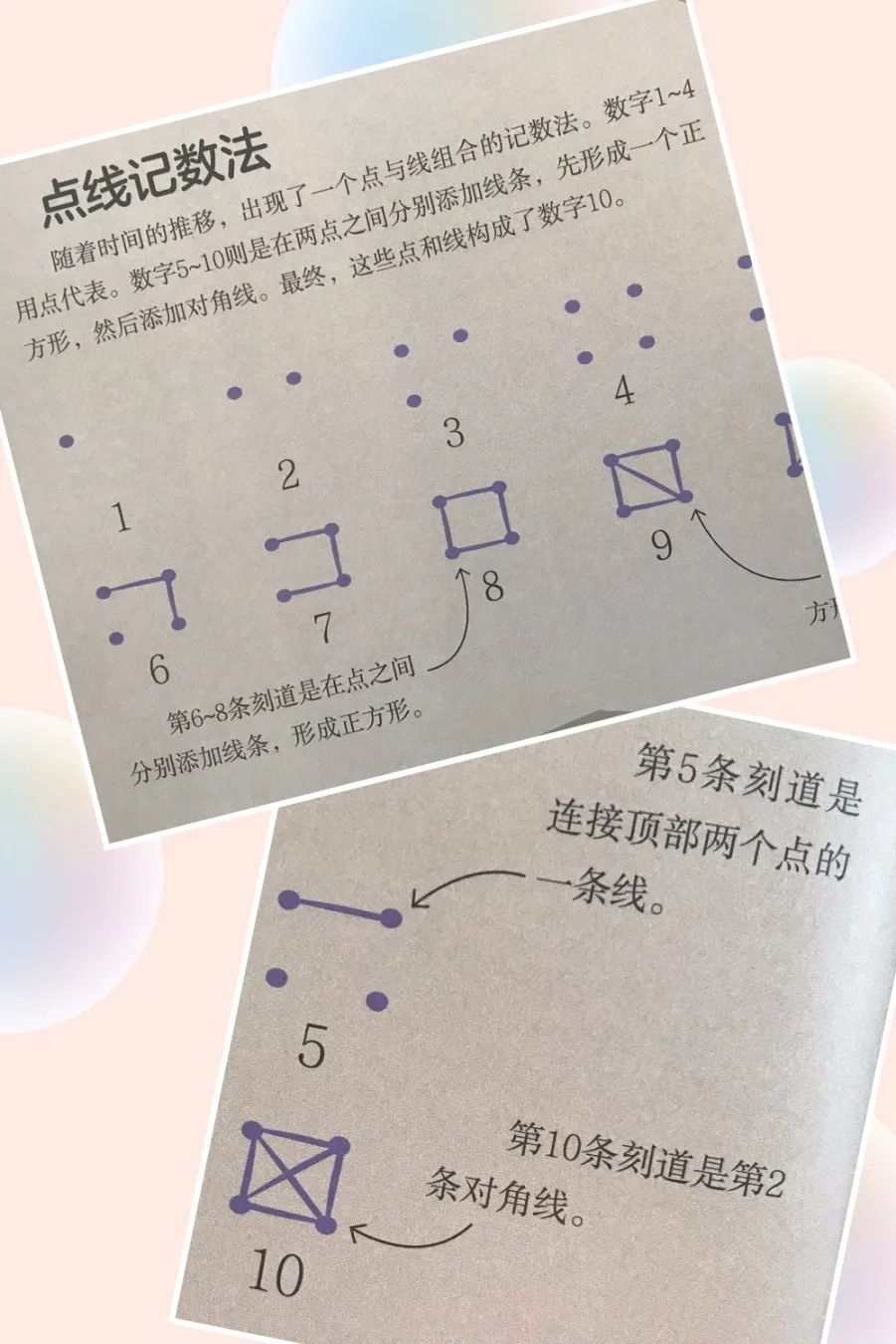
正字计数法(写“正”字)
对大家来说再熟悉不过了!这可是咱们中国人自己发明的,从古至今一直沿用,就连西方人看了也很容易理解。记得以前班里选班干部投票计数,用的都是这个方法!

当人类掌握了如何运用符号来记录数目,紧接着就要开始学着进行计算。也就是我们说的计数。
而这个记数——计数的演变对古人来说也并非易事。
最开始可想而知,早期的人类一定是用自己的手脚来计数的。(这和我们教小宝宝学数学的场景是不是很像呢?)
所以,现在我们使用的是十进制计数系统,也被称为基数为10的计数系统,表示以10为一组进行思考和计数。

而美洲的玛雅文明和阿兹特克文明使用的是基数为20的计数系统,这个计数系统可能是根据手脚并用后的结果!

而聪明的古巴比伦人使用的是以60为基数的记数系统。他们利用手指关节,貌似还结合了倍数的概念。而现在我们仍然在使用六十进制系统,每分钟有60秒,每小时有60分钟,都是源于古巴比伦人的智慧。

巴布亚新几内亚的某些部落使用的以27为基数的记数方法看着也很有趣。他们把人的上半身从手指到关节、到肩膀、到眼睛、到鼻子甚至耳朵全都用上数数了。看看下图,是不是很有意思呢?

说到纵向思维,那必须要对事物的变化发展有清晰的时间概念。
因此,清晰的时间线提示也是本书的一大亮点。有了纵向的时间对比,孩子在读起书来思路清晰,对数学的演变发展一目了然。
比如,书里讲关于数字“0”的故事。如果不是有着清晰的时间线,我们常人根本不会想到0,这样一个看似简单但却意义非凡的一个数字从被人开始记录、到接受、到搞清运算规则、到后期传播、到广泛被应用在计算当中,竟然经历了几千年!

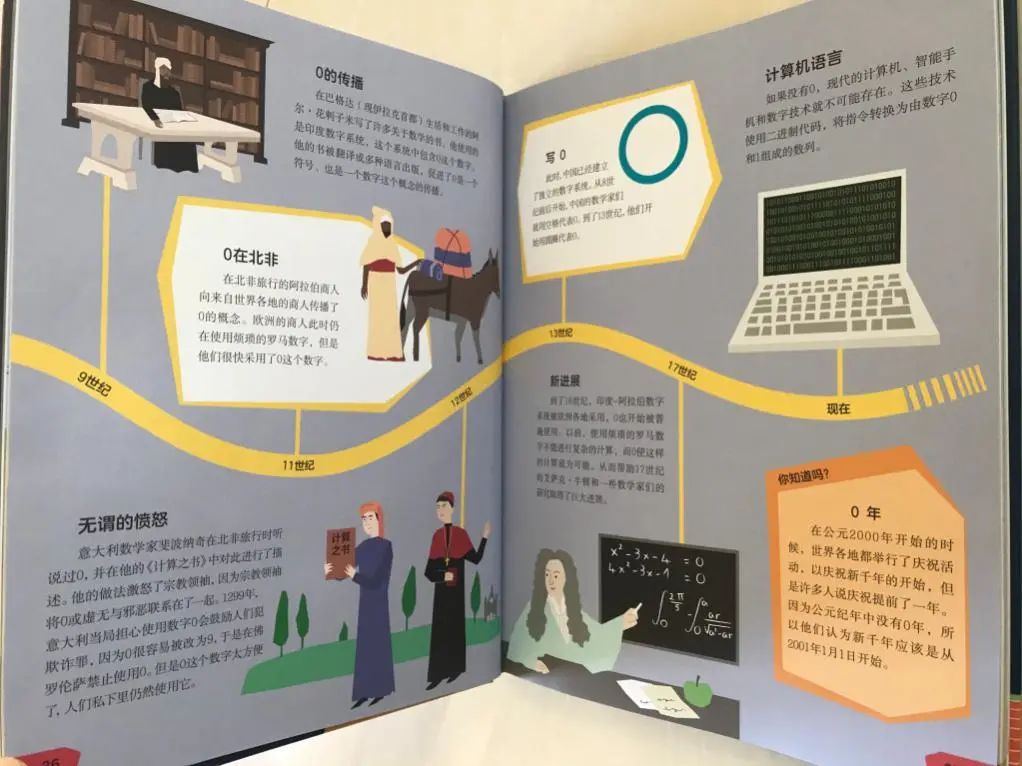
而到后期讲人类如何计算大数的时候,从最早苏美尔人(约公元前2700年)发明算盘、到齿轮计算机出现、纳皮尔筹计算系统的设计、计算尺的发明、税收计算器的制作、一直到19世纪电子计算机的出现、互联网的诞生、超级计算机的使用等等,都有清晰的时间路线让孩子清楚的感受到人类研究数学历史的发展以及数学是如何改变了我们的世界。


在随着本书穿越数学历史长河的同时,也不禁让人感慨。几千年来,人类文明的演变、科学每一次的推陈出新,世界每次经历的技术变革,都汇聚了人类的无穷无尽的智慧!
之前跟大家介绍了,孩子阅读这本书,也相当于看数学的历史故事。这里面出现的各种时期的文明,非常有必要让孩子了解。
我在和孩子读这本书的时候,发现开篇讲人类计数的历史最先是要追溯到非洲的。而这时候孩子会好奇的问我:“为什么会是最落后的非洲?而不是发达的北美或者欧洲?”
为了解答这个问题,我特意又带孩子看了一遍《人类简史》的绘本,里面记录着:“数百万年前,最早的人类出现在非洲大陆…”
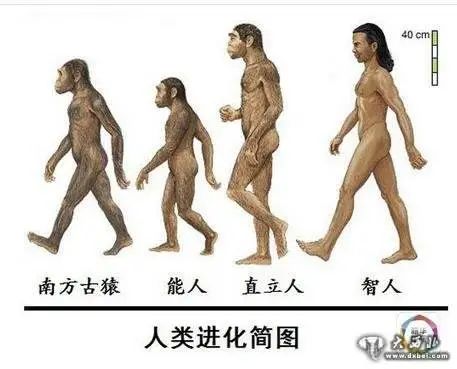
人类进化简图
所以你看,我们虽然在和孩子读数学历史,但又间接地回顾了关于人类起源的知识。
而书里多次出现了玛雅文明、古巴比伦文明、苏美尔文明、古埃及文明、古罗马文明等等。如果说古埃及文明与古罗马文明孩子们理解起来倒是不难,毕竟听起来埃及、罗马这两个地方在地图上还有标注,可是玛雅文明、古巴比伦文明、苏美尔文明,就需要我们借助外部资料进行内容扩展。

这几个文明的出现、兴盛、及消亡究竟是怎么回事?那些神奇的语言究竟是真是假?我在这里不多说了,感兴趣的家长可以试着带孩子一起做一张大表进行对比,完工后相信你们都会有不小的收获!没准,孩子对世界史的兴趣,就是从这里开始的!当然,做研究的时候别忘了还要加上中国和印度~
了解了数学,就会开启孩子“十万个为什么”的话匣子。紧接着,书里提到的关于“远古非洲人是如何计算时间的?“,几何是怎么来的?”“如何利用对称性?” “怎样测量金字塔的高度?”,“如何估算人口?”、“如何运用数据改变世界”等等的问题就会接踵而至。
而面对一个个抽象的话题或是概念,家长们不免都会犯难。但好在这本书都能够将难理解的概念简单化。每一个新的概念,书里都会
引用故事或者接地气的解说来帮助大家理解。
比如,负数的概念对于孩子来说很抽象,但进行负数运算最简单的方法其实是在数轴上画出负数!

而正、负数的加减法用画数轴理解起来也更为直观!

再比如讲“等比数列”的问题,书里会引用一个聪明的旅行者与国王下棋,赢了之后用“等比数列”的概念要求国王赏赐大米。他要求国王在棋盘山的每一个格子中按照第一格放一粒、第二格放两粒以此类推…起初国王不以为然,可随着数字不断加倍,后期结果惊掉国王下巴的故事。

再比如,书中讲解了古人的几种计数方法。,也会出一道迷题,让孩子们用这几种方法进行计算。(答案在书后有)

你还可以与孩子化身小特工,尝试玩摩尔斯电码,发送例如“I love u”进行解码演习,看谁能够最先破译密码!

孩子可能会问了,难道数学仅仅是这些发明,以及每日的纸面刷题吗?当然不是了!数学早已融入了我们生活的方方面面,解决生活的实际问题。
这本书还有一大妙处,就是告诉你数学(包含几何)在人类的生活中,究竟能解决什么样的问题。
比如:中国最早发明了结合阴历和阳历的综合历法,对农耕有着重要意义。

而早在4000年前,聪明的古巴比伦人和埃及人就已经开始研究几何学了。几何学可是建筑和天文学等众多领域的重要组成部分!作为数学最古老的分支之一,研究形状、大小和空间的几何学能够帮助我们了解周围的世界。
比如自然界中随处可见的对称事物,这种简单有序的美被设计师、艺术家和建筑师充分利用,印度的泰姬陵就是最好的例子。

而古希腊数学家泰勒斯利用三角形的秘密,破解出了金字塔的高度(如今我们依旧在使用“
三角形定位法
”来找到你手机的位置)


不仅如此,人类甚至还利用“密码”的知识,将自己的信息传递到了外太空!
原来,在1974年,科学家们从波多黎各的阿雷西博天文台向距离地球25000光年的武仙座球状星团M13发送了一条无线电信息,希望被外星人接受并阅读。这条信息是用二进制代码编写的。
在二进制系统中,只采用1和0两个数码。如果用图片展示,看起来就是下面这样:
























