泊松自助法（Poisson Bootstrap Sampling）：大型数据集上的自助抽样

来源：DeepHub IMBA
本文约4500字，建议阅读10+分钟
经典自助抽样是一种非常有效的技术，可以用于从收集的样本中学习统计量的分布。

自助抽样可以根据收集的样本推断总体的统计特征(如均值、十分位数、置信区间)。泊松自助抽样（Poisson Bootstrap Sampling）是一种用于统计分析中的重采样技术，特别是在机器学习和数据科学中用于模型评估和误差估计。这种方法的一个特点是保留了样本中数据点出现的自然波动，而不是像传统的自助法那样平均采样，因此在某些特定应用中更为准确。

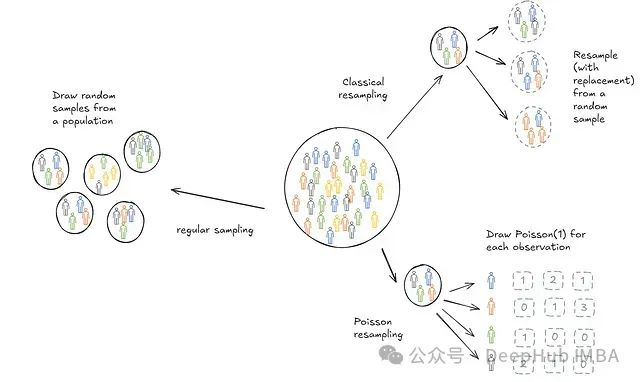
为了深入研究泊松自助法，我们首先来介绍经典的自助抽样方法。

经典自助抽样

假设我们想计算一所学校学生的平均年龄。我们可以重复抽取100名学生的样本,计算平均值并存储。然后对这些样本均值取最终平均值。这个最终平均值是总体平均值的估计。

但是在实际应用时从总体中重复抽取样本通常是不可能的。所以就发明乐自助抽样法，自助抽样某种程度上模仿了这个过程。我们不是从总体中抽取样本,而是从我们收集的一个样本中抽取样本(有放回)。这些伪样本被称为重采样。

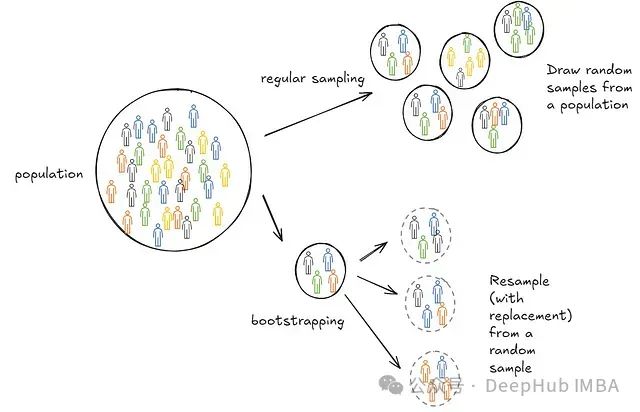
这种方法非常有效。虽然比封闭形式的解决方案在计算上更昂贵,但它不需要对总体分布做强假设。另外它也比重复收集样本更便宜。所以它在实际工作中被广泛使用,因为在许多情况下,要么不存在封闭形式的解决方案,要么很难得到正确的结果——例如,在推断总体的十分位数时。

自助抽样（Bootstrap Sampling）的有效性源于其通过重采样的方法来模拟数据的变异性，进而对统计估计的稳定性和不确定性进行评估。这种方法有效的原因包括以下几个方面：

1. 无需对数据分布的假设

传统统计推断通常依赖于对数据分布的假设，如正态分布。而自助抽样不依赖这些假设，而是直接从原始数据中进行重采样。这意味着自助抽样适用于更广泛的数据类型和分布情况，即使在不知道数据分布的情况下也能提供有效的估计。

2. 反映数据中的自然变异性

自助抽样通过从原始样本中有放回地抽取数据，生成多个新的样本。这些重采样的样本捕捉了原始数据的自然变异性，从而允许估计不同统计量的分布，例如均值、方差、回归系数等。这种方法反映了样本中数据点的多样性，能够更好地估计统计量的精度和不确定性。

3. 样本内估计

自助抽样在每次重采样时随机生成的新样本类似于从总体中再次抽样，允许在样本内进行推断。通过对重采样的多个样本进行统计分析，可以获得参数的分布，从而评估估计量的方差和构建置信区间。

4. 适用于小样本或复杂模型

自助抽样尤其适用于小样本数据和复杂模型。在这些情况下，传统统计方法可能无法准确估计参数的不确定性。而自助抽样通过重采样方法，可以有效地评估小样本中统计量的稳健性，提供更加可靠的推断结果。

5. 泛化到多种统计问题

自助抽样方法具有极大的灵活性，适用于各种统计问题，如参数估计、模型选择、误差分析等。它不仅可以用于简单的均值和方差估计，还可以用于复杂模型的预测误差估计，甚至用于非参数统计推断。

经典自助抽样演示

我们将用两个例子来解释自助抽样。第一个是一个小型数据集,其中的想法是你可以在头脑中进行计算。第二个是一个较大的数据集,我会为此写下代码。

示例1：确定学校学生的平均年龄

我们的任务是确定一所学校学生的平均年龄。我们随机抽样5名学生。这个想法是使用这5名学生来推断学校所有学生的平均年龄。这在统计上不恰当并且听起来就很愚蠢,但是这足以说名自助抽样的优势。

 ages = [12, 8, 10, 15, 9]

现在我们从这个列表中有放回地抽样。

 sample_1 = [ 8, 10, 8, 15, 12]   sample_2 = [10, 10, 12, 8, 15]   sample_3 = [10, 12, 9, 9, 9]   ....   do this a 1000 times   ....   sample_1000 = [ 9, 12, 12, 15, 8]

对每个重采样计算平均值。

 mean_sample_1 = 10.6   mean_sample_2 = 11   mean_sample_3 = 9.8   ...   mean_sample_1000 = 11.2

对这些平均值取平均。

 mean_over_samples=mean(mean_sample_1, mean_sample_2, .. , mean_sample_1000)

这个平均值然后成为你对总体平均值的估计。下面就可以对任何统计属性做同样的事：置信区间、偏差等。

示例2：确定"支付处理时间"的95百分位数

食品外卖应用程序的客户在应用程序上进行支付。支付成功后，订单会发送给餐厅。支付处理时间计算为客户按下"支付"按钮到收到反馈（支付成功、支付失败）之间的时间，这是反映平台可靠性的关键指标。每天有数百万客户在应用程序上进行支付。

我们的任务是估计分布的95%百分位数，以便能够快速检测问题。

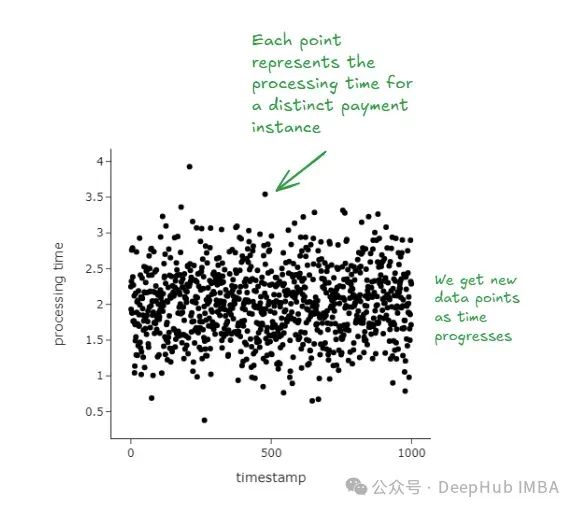
我们试用以下方式说明经典自助抽样：

我们假设有一个包含一百万个观测值的总体。在现实世界中，我们从不观察这些数据。随机抽取总体的1/10。所以取10,000个观测值，这是我们唯一观察到的数据。然后应用上面讨论的相同程序，从我们观察到的数据中有放回地重新抽样，并多次重复这个过程。每次重新抽样时，计算该分布的95百分位数。最后取95百分位数值的平均值，并找出其周围的置信区间。

得到了下面的图表。神奇的是，我们发现刚刚生成的置信区间包含了真实的95百分位数（来自总体）。

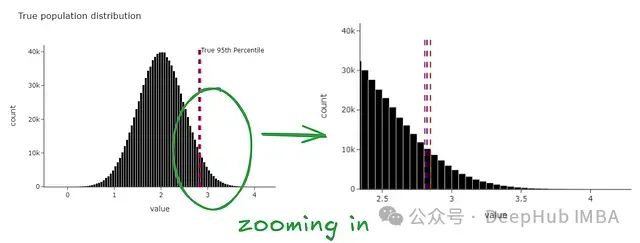
我们可以在自助抽样统计量的层面上看到相同的数据。

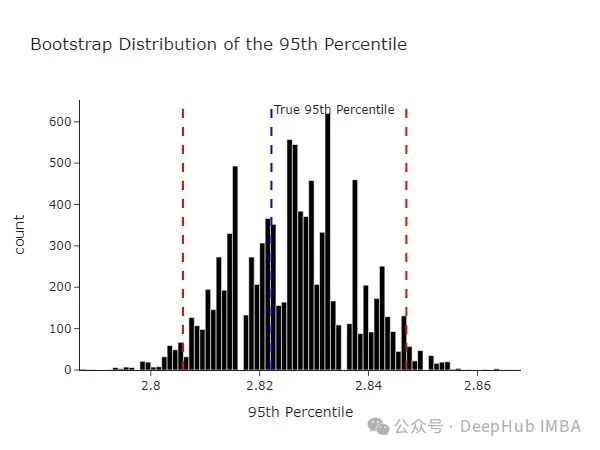
生成上述内容的代码如下：‍‍

 def bootstrap_nth_percentile_and_ci(    data: List[float], n_iter: int = 1000, alpha: float = 0.95, percentile: float = 95) -> Tuple[float, float, float, float]:    """Compute the nth percentile and confidence interval using bootstrapping   Args:       data (List[float]): List of data       n_iter (int, optional): Number of bootstrap samples. Defaults to 1000.       alpha (float, optional): Confidence level. Defaults to 0.95.       percentile (float, optional): Percentile to compute. Defaults to 95.    Returns:        Tuple[float, float, float, float]: Tuple containing the percentile, mean,        lower bound, and upper bound    """      n = len(data)      bootstrap_samples = np.random.choice(data, (n_iter, n), replace=True)     percentiles = np.percentile(bootstrap_samples, percentile, axis=1)      mean = percentiles.mean()     lower = np.percentile(percentiles, (1 - alpha) / 2 * 100)     upper = np.percentile(percentiles, (1 + alpha) / 2 * 100)      return percentiles, mean, lower, upper   # population specifics mean_time = 2.0 std_dev = 0.5 processing_time = np.random.normal(loc=mean_time, scale=std_dev, size=1_000_000)  # sample from processing time sample = np.random.choice(processing_time, 10000) # note we only sample 1/10th of the population  percentiles, mean, lower_bound, upper_bound = bootstrap_nth_percentile_and_ci(     sample, n_iter=10000, percentile=95 )

现在我们已经确立了经典自助抽样确实有效，我们将尝试从数学角度说明正在发生的事情。

泊松自助抽样

现在让我们思考一个游戏。想象你有一个装有5个球的袋子：一个红球、蓝球、黄球、绿球和紫球。你需要从袋子里一次抽一个球，总共抽5次。每次抽完一个球后，你把它放回袋子，然后再抽。所以每次选择一个球时，都有5个不同颜色的球可以选择。每轮结束后，你在一个空槽中记录所选择的球（如下所示）。

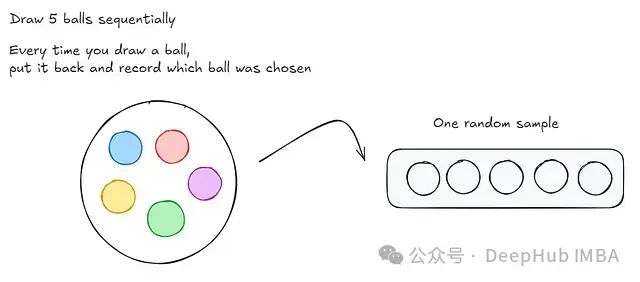
现在，每个球被选中填入每个槽的概率是多少？

对于槽1：

• 红球被选中的概率是1/5
• 紫球被选中的概率是1/5
• 绿球被选中的概率是1/5
• 蓝球被选中的概率是1/5
• 黄球被选中的概率是1/5

同样的情况也适用于槽2、3、4和5：

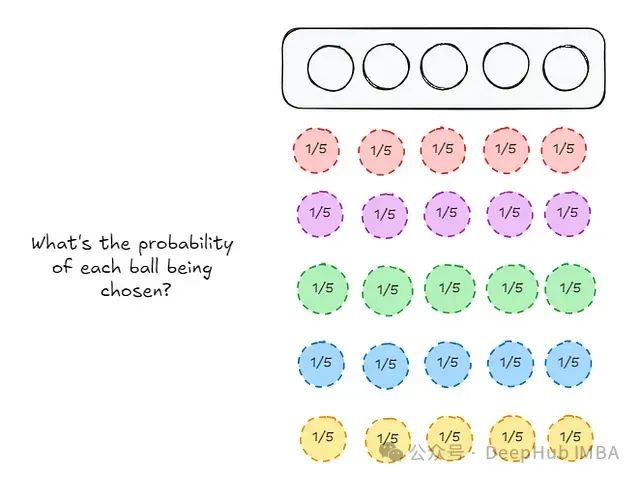
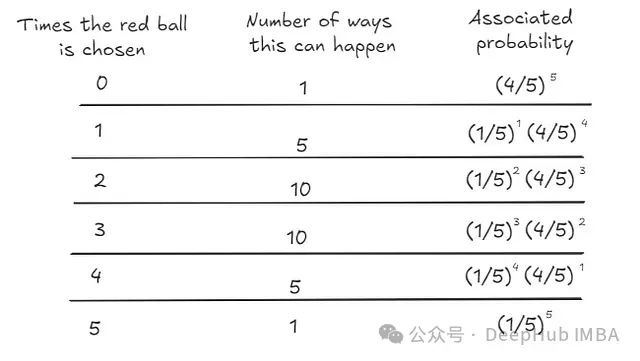
让我们稍微关注一下红球。它可以被选中的最少次数是零次（完全没有被选中），最多次数是5次。红球出现的概率分布如下：

• 红球被选中0次：这只能以1种方式发生。
• 红球被选中1次：这可以以5种方式发生。红球被选中填入槽1，红球被选中填入槽2...（你明白了）。
• 红球被选中2次：这可以以10种方式发生。将红球固定在槽1，有4个选项。将红球固定在槽2，有3个新选项，...
• 红球被选中3次：这可以以10种方式发生。这与上面的逻辑完全相同。
• 红球被选中4次：这可以以5种方式发生。类似于被选中1次。
• 红球被选中5次。这只能以1种方式发生。

这就是 5选k ，其中 k = {0, 1, 2, 3, 4, 5}。

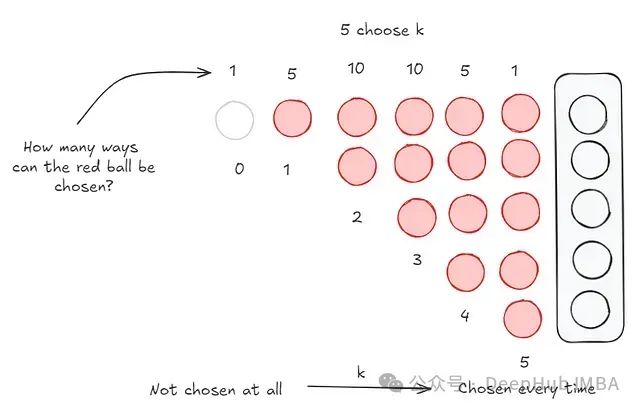
让我们只对红球来进行讨论。

上面描述的是二项分布，其中 n = 5 且 p = 1/5。

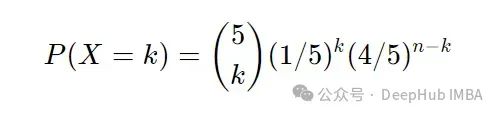
或者更一般地，

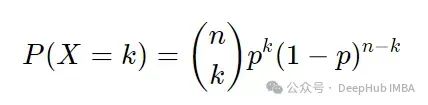
现在我们只需将球替换为观测值。

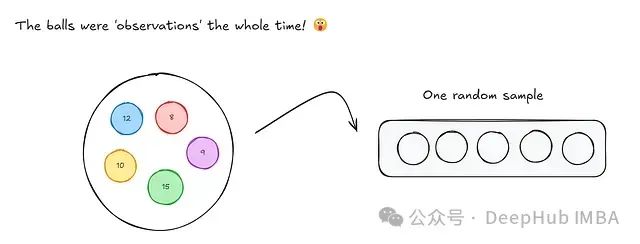
所以当我们进行自助抽样时，实际上是从二项分布中抽取每个观测值。

在经典自助抽样中，当我们重新抽样时，每个观测值都遵循二项分布，其中 n = n，k = {0, ..., n} 且 p = 1/n。 这也表示为 Binomial(n , 1/n)。

而二项分布的一个非常有趣的性质是，当n变得越来越大，p变得越来越小时，二项分布收敛到参数为 Poisson(n/p) 的泊松分布。

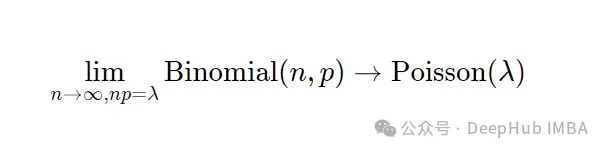
这适用于任何n和p，只要n/p是常数。在下面的gif中，我们展示了lambda (n/p) = 5的情况。

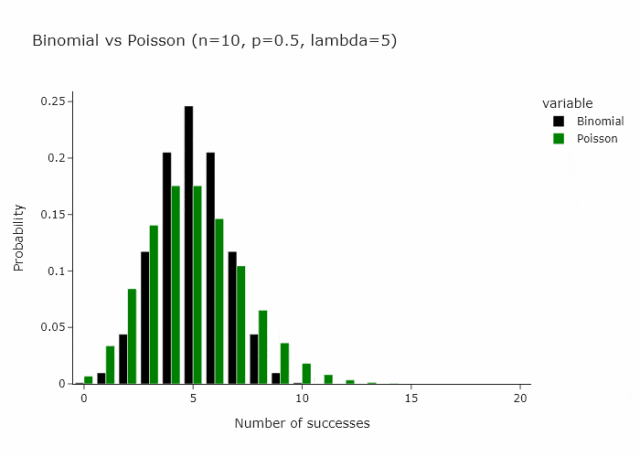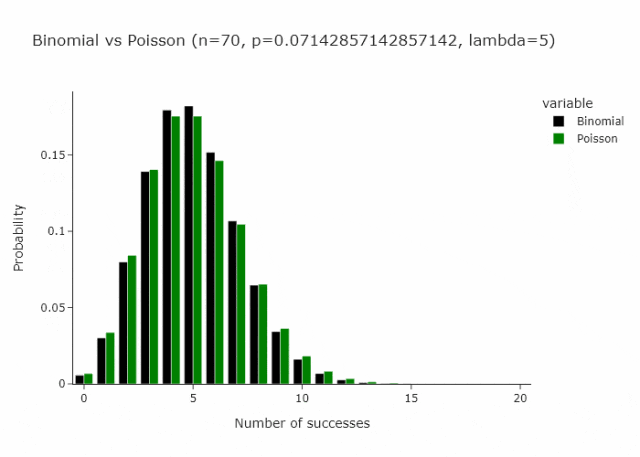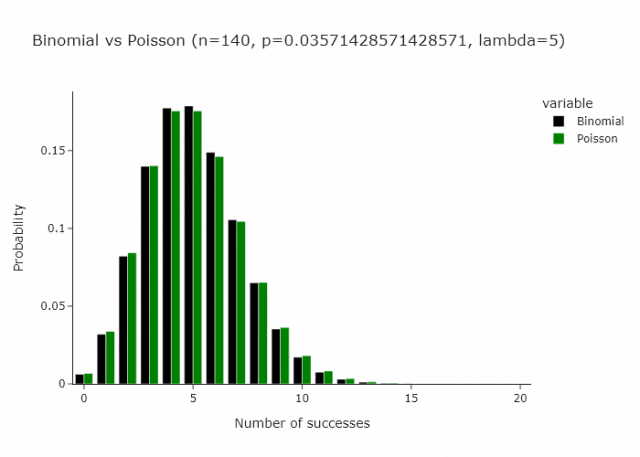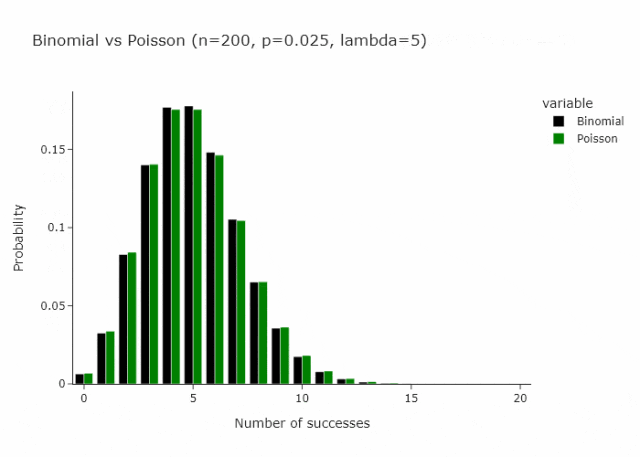
在我们定义的这种特殊情况下，由于p只是1/n将收敛到 Poisson(1)。

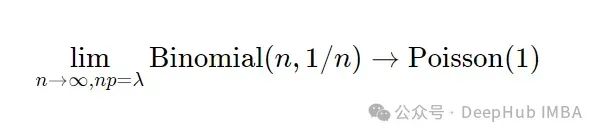
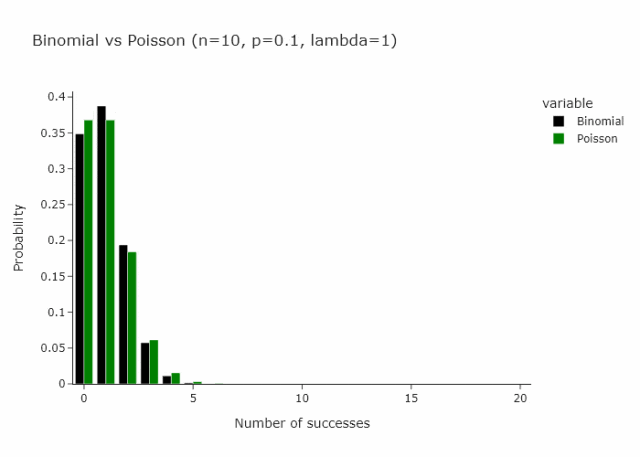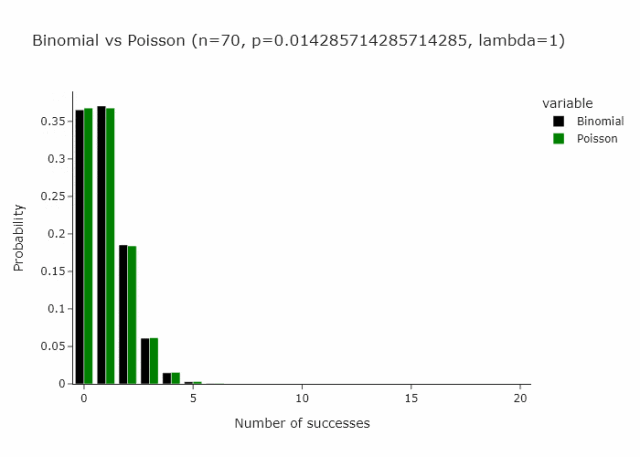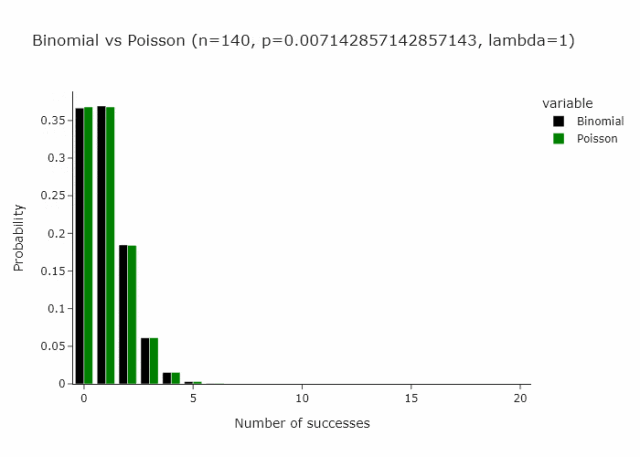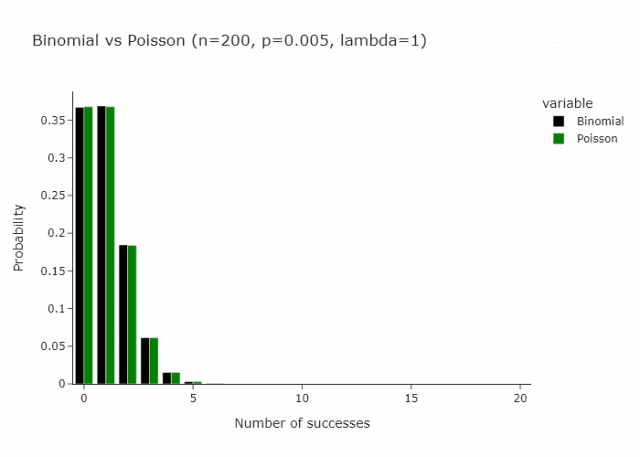
这就变成了另一种重新抽样的方法：从 Poisson(1) 分布中抽取每个观测值。

泊松自助抽样意味着我们使用 Poisson(1) 过程来生成用于自助抽样统计量的重采样。

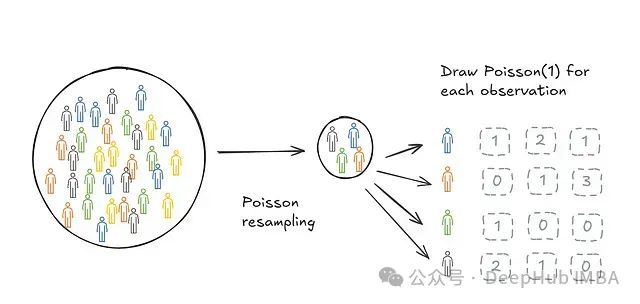
这为什么这有用？

对感兴趣的统计量进行自助抽样有两个阶段。第一阶段是创建重采样，第二阶段是在每个重采样上计算统计量。经典自助抽样和泊松自助抽样在第二阶段是相同的，但在第一阶段不同：

泊松自助抽样减少了我们需要对数据进行的遍历次数；泊松自助抽样适用于没有固定n的情况。例如，当我们在流式传输数据时。

在重采样时减少遍历次数

泊松自助抽样在创建重采样时允许显著的计算收益。查看这一点的最好方法是通过代码。

 def poisson_bootstrap_nth_percentile_and_ci(     data: List[float], n_iter: int = 1000, alpha: float = 0.95, percentile: float = 95 ) -> Tuple[float, float, float, float]:      data = np.array(data)     n = len(data)      weights = np.random.poisson(1, (n_iter, n))      percentiles = []      for weight in weights:         resampled_data = np.repeat(data, weight)         percentile = np.percentile(resampled_data, 95)         percentiles.append(percentile)      mean_percentile = np.mean(percentiles)     lower_bound = np.percentile(percentiles, (1 - alpha) / 2 * 100)     upper_bound = np.percentile(percentiles, (1 + alpha) / 2 * 100)      return percentiles, mean_percentile, lower_bound, upper_bound

比较上面的第(8)行与经典自助抽样中的等效行：

 # 经典，需要知道(data)   bootstrap_samples = np.random.choice(data, (n_iter, n), replace=True)      # 泊松，不需要知道(data)   weights = np.random.poisson(1, (n_iter, n))

在经典自助抽样中，你需要知道 data，而在泊松自助抽样中你不需要。

对于数据非常大的情况（想想上亿个观测值），这种影响非常显著。这是因为从数学上讲，生成重采样归结为为每个观测生成计数。

• 在经典自助抽样中，每个观测的计数遵循 Binomial(n, 1/n)。它们一起遵循 Multinomial(n, 1/n, 1/n, ..., 1/n)。这意味着当为一个观测生成计数时，会影响其他观测的计数。例如，在我们的球的例子中，一旦你为红球生成了计数，这就直接影响了其他球的计数：如果红球的计数是2，那么我们知道只能再选择3个球。

• 在泊松自助抽样中，每个观测的计数是相互独立的。所以如果你需要1000个重采样，你只需为红球生成1000个 Poisson(1) 抽样。然后就完成了，可以移动到下一个观测。

当n未知时的重采样

有些情况下n实际上是未知的。例如，在你正在流式传输支付数据的情况下，或者数据非常大以至于分布在多个存储实例中的情况下。

在经典自助抽样中，每次观察到n增加时，都必须重新进行重采样过程（因为我们是有放回抽样）。这使得这种方法在计算上相当昂贵且浪费。而在泊松自助抽样中，我们只需为每个实例保存我们的 Poisson(1) 抽样。每次添加新实例时，只需为这个新实例生成 Poisson(1) 抽样。

总结

经典自助抽样是一种非常有效的技术，可以用于从收集的样本中学习统计量的分布。而对于非常大的数据集，它可能会非常昂贵。泊松自助法的每次抽样可以独立进行，非常适合在分布式系统中并行化处理。在分布式环境中，不同的计算节点可以独立地生成泊松抽样，从而加快处理速度。

泊松自助法避免了传统自助法中可能出现的冗余问题（即部分数据点在所有重采样中都出现，导致缺乏多样性），因为泊松抽样允许某些数据点完全不被选中，从而保留了数据的多样性。对于不平衡数据集，泊松自助法能够更自然地反映数据的原始分布，从而在重采样过程中保留数据的特性。

在泊松自助抽样下重采样意味着我们只需对每个观测进行一次遍历。在流数据情况下，泊松自助抽样允许我们增量处理新的重采样，而不是必须一次性对整个数据集进行重采样。相比于传统的自助法，泊松自助抽样在某些情况下可以提供更精确的估计，特别是在高维数据或复杂模型中。

作者：David Clarance