技术专栏丨全能ADC，你应该这样用（连载 中）

之前我们分享了该系列博客前两篇，主要介绍了两个问题

• 如何与小于ADC输入范围的单极性输入源接口？

• 为何要配置ADC驱动器？

点击可查看→ 全能ADC，你应该这样用（连载 上） 即可查看。

今天，我们来看看该系列博客的第三篇和第四篇—— 同相求和配置 以及 支持衰减的同相求和配置。

双极性信号在低电压(0 V)上下摆动。由于 ADAQ798x 集成 ADC 只能转换0 V 到 V _REF 的信号，所以针对该 ADC，需要将双极性信号加以直流偏置和适当调整。为了完成这一任务，以下配置给标准同相配置增加了两个电阻（R ₁ 和R ₂ ）。

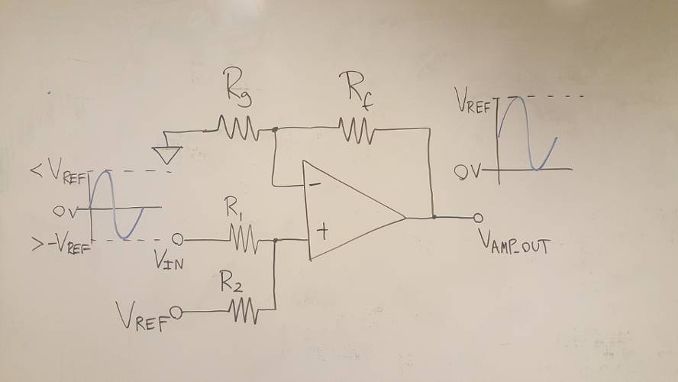
此配置将输入信号与一个单独的直流电压求和，以将ADC驱动器输出偏置到ADC中间电平输入(V _REF /2)，从而实现双极性到单极性的转换。基准电压(V _REF )用作直流电压常常是可行的，这样就无需其他电路（反正ADAQ798x总是伴随一个基准电压源！）。它还能防止V _REF 偏差给系统增加失调误差，因为ADC驱动器的直流偏置总是V _REF 的一半。鉴于这些原因，我们将专门讨论这种将V _REF 用作直流“变换”电压的配置。

此配置的传递函数如下：

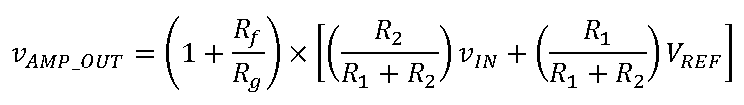
与普通同相配置类似，R _f 和R _g 之比决定从IN+到AMP_OUT的增益，但此比值现在也依赖于v _IN 的输入幅度。注意v _IN 为双极性，但同相节点上的电压为单极性。这意味着，对应于v _IN 的最小值，IN+上的电压必须为0 V：

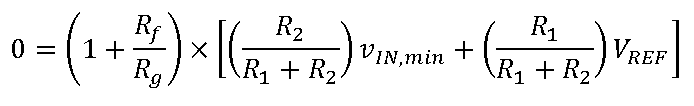
由此关系可得出R ₁ 和R ₂ 之比：

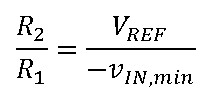
R _f 和R _g 可利用该配置的传递函数以及v _IN 为0 V时ADC驱动器输出(v _{AMP_OUT} )等于V _REF /2的条件来确定。求解R _f 和R _g 的方程可得：

现在有了R ₁ 和R ₂ 之比及R _f 和R _g 之比，但我们还需要挑选特定的值。我们已在该系列博客《增加单极性输入的增益》中讨论了R _f 和R _g 值的选择。R ₁ 和R ₂ 的选择应基于应用的噪声、精度和输入阻抗要求确定。小电阻会改善噪声，可降低其与ADC驱动器输入偏置电流相互作用所引起的失调误差，但若要提高输入阻抗并降低基准源的输出电流，则需要大电阻。此电路的输入阻抗为：

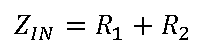
注意，对于v _IN 幅度为±V _REF 的特殊情况，R _f 和R _g 之比为0。这种情况下，ADC驱动器增益为1，意味着省去R _g ，R _f 可以为0 Ω。

举例说明

ADAQ7980需要对±1 V输入信号执行双极性到单极性转换，V _REF = 5 V，使用R _f = 2 kΩ。利用上述公式，R ₂ 须为R ₁ 的5倍，R _f 须为R _g 的2倍。R _f 为2 kΩ，所以R _g 须为1 kΩ。R ₁ 和R ₂ 的具体值可根据应用要求选择。对于本例，我们希望选择R ₁ 和R ₂ 的组合来抵消输入偏置电流对失调误差的影响。技术文章 《运算放大器输入偏置电流》 中已经阐明，为实现此目的，R ₁ ||R ₂ 应等于R _f ||R _g ，故R ₁ = 800 Ω，R ₂ = 4 kΩ。

我们再考虑一个例子：v _IN = ±10 V，V _REF = 5 V。这种情况下，我们会遇到R _f 和R _g 之比为负数的问题，所以利用这种配置实际上不能实现该输入范围。事实上，适合此配置的最大v _IN 为±V _REF ，此时ADC驱动器增益等于1。幸运的是，我们会在本系列接下来的文章中讨论其他两种允许我们超出此输入范围的配置。

若将R ₂ 接地而不是接V _REF ，则以上配置也可用于单极性信号。这一修改对需要衰减以用于ADC的单极性输入信号（幅度大于V _REF ）有用。这种情况下，ADC驱动器极有可能是单位增益，故不需要R _f 和R _g 。

如上所述，如果应用要求高输入阻抗，则R ₁ 和R ₂ 必须很大，这可能会提高系统的本底噪声。我们可以通过增加分流电容和/或通过过采样和抽取来补偿噪声增加。两种方案均通过损失输入信号带宽来降低本底噪声。但是，对于低带宽或直流应用，输入带宽不那么重要。因此，这些配置更适合低带宽、高输入阻抗应用。我们将在下一篇文章中更详细讨论这个话题。

然而，有一个问题未涉及，那就是ADC驱动器流过电阻的输入偏置电流所引起的失调误差。电阻越大，引起的直流误差越大。通过调整R ₁ 和R ₂ 之比以补偿不需要的压降，或通过选择R _f 和R _g 的值来抵消R ₁ 和R ₂ 引起的失调，可以降低此误差，不过输入范围会有损失。但应注意，R _f 必须足够小以确保放大器稳定，故第二种方案并不总是可行。

针对大于±V _REF 的信号，可采用以下配置来执行带衰减的双极性到单极性转换。

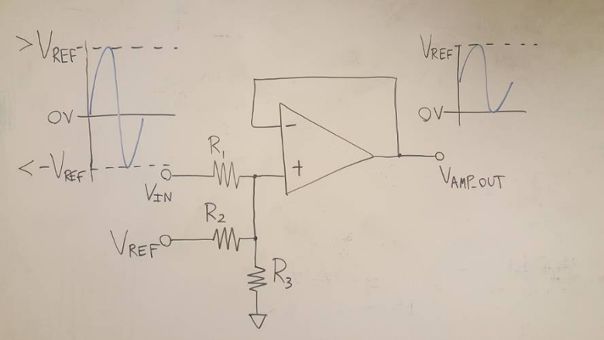
此配置与上文的【同相求和配置】讨论的配置相似，区别在于不再需要R _f 和R _g ，但增加了R ₃ 以提供额外的信号衰减。此配置的传递函数如下：

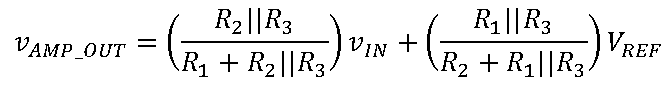
这次求得R ₁ 、R ₂ 和R ₃ 之比的数学计算较为复杂，但我们可以使用同之前配置相似的方法。求出电阻之比后，便可根据应用需求选择具体的值。为了简洁起见，这里不叙述推导的每一步，但我们会看到，对于v _IN 的最小值和最大值，传递函数的简化使我们能得出电阻比。

R ₁ 和R ₂ 之比是利用该配置的传递函数并代入v _IN 最小值（使得v _{AMP_OUT} 等于0 V）而得出：

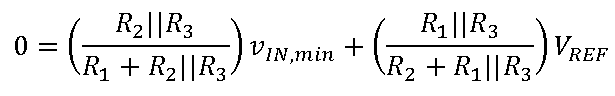
R ₃ 不出现在公式中，求解R ₁ 和R ₂ 得到：

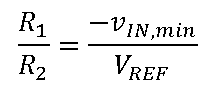
R ₁ 和R ₃ 之比是代入v _IN 最大值（使得v _{AMP_OUT} 等于V _REF ）而得出：

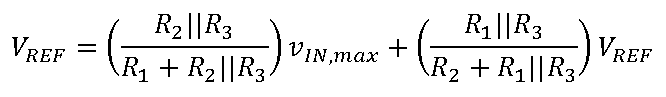
这一次，R ₂ 不出现，求解R ₁ 和R ₃ 得到：

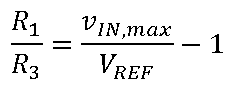
此时，我们可以选择其中任一电阻的值（考虑V _REF 和v _IN 范围），然后计算另两个电阻的值。像以前一样，主要权衡因素是输入阻抗与系统噪声和失调误差。此电路的输入阻抗(Z _IN )为：

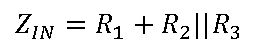
再次考虑该上文【同相求和配置】部分的例子，其中v _IN = ±10 V，V _REF = 5 V，用1 MΩ的输入阻抗设计该配置。对于v _IN 和V _REF 的这种组合，R ₁ 须为R ₂ 的2倍，且等于R ₃ 。将R ₂ 和R ₃ 与R ₁ 的比值用于输入阻抗公式，得到R ₁ = 750 kΩ。因此，R ₂ 和R ₃ 分别为375 kΩ和750 kΩ。

正如上文【同相求和配置】所述，需要权衡输入阻抗与系统噪声性能。实现高输入阻抗需要大电阻，而后者会产生更多热噪声，并与ADC驱动器的输入电流噪声相互作用，产生更多输入电压噪声。二者均会提高ADC输入端的有效均方根电压噪声，导致性能大幅降低。在上例中，系统总噪声约为334 μV rms（使用5 V基准源时，动态范围降低整整15.5 dB，从92 dB降至74.5 dB）！

但还有希望！如果限制输入带宽，这种配置实际上可以实现接近最优的性能。例如，若将上例中的输入带宽限制为20 kHz，则全系统噪声几乎降低10倍，达到48 μV rms（对于V _REF = 5 V，动态范围为91.4 dB）！我们可以通过增加分流电容C _S 来限制输入带宽(BW _in )，如下图所示。注意，对于这些噪声计算，我们可以将R ₁ 、R ₂ 和R ₃ 看作单个电阻R _S ，其中R _S 为R ₁ 、R ₂ 和R ₃ 的并联组合。