前前言
昨天下午我早早的打扫好卫生,煮好饭菜,iPad 充满电,给了老婆一笔购物基金打发出去shopping,准备见证 LPL 的三连冠,但没想到,技不如人,再一次在主场丢失了冠军,气的我又又
又又
又又
一次卸载了英雄联盟,玩起了单机游戏。
前言
今天的主题十分有趣,我们将在
我的世界(Minecraft)
这个游戏里,靠一个个逻辑门来组合实现一个简单的七段显示器,可以实现将选择的数字输出在显示器上。
演示视频在下面,来看看这个宏大的工程:
接下来,我会从最基础的
与或非
实现开始,亲自画出
电路原理图
,并且用
我的世界
来带领大家领略数字电子技术的精妙之处。
本文所涉及的
数电知识
包括
电路编码
、
基本逻辑门
、
组合电路
。
当然,由于电路的精密性以及游戏里实现的复杂性,实现完整的电路是非常困难的,也会让人难以看懂,一下子就劝退了,这也就违背了我们学习知识的初衷。
所以,我会适当的对电路进行化简,让人看起来简单易懂。
在这个过程中,我相信你一定会加深对数电的认识。学好数电,对更好更快地理解计算机组成,乃至于我们吸收软件知识都十分有帮助。
准备工作
二进制编码
我们首先复习一下电路是如何传输十进制。
当你在电路里传输一个十进制数时,肯定要先转成二进制,一般有
两种二进制编码形式
,分别是自然二进制码和 BCD 码。
自然二进制码
这是人们常说二进制码,用
除二取余
进行真实的转化,也就是自然二进制。
我们举个例子,用除二取余法将十进制 123 转换成二进制:
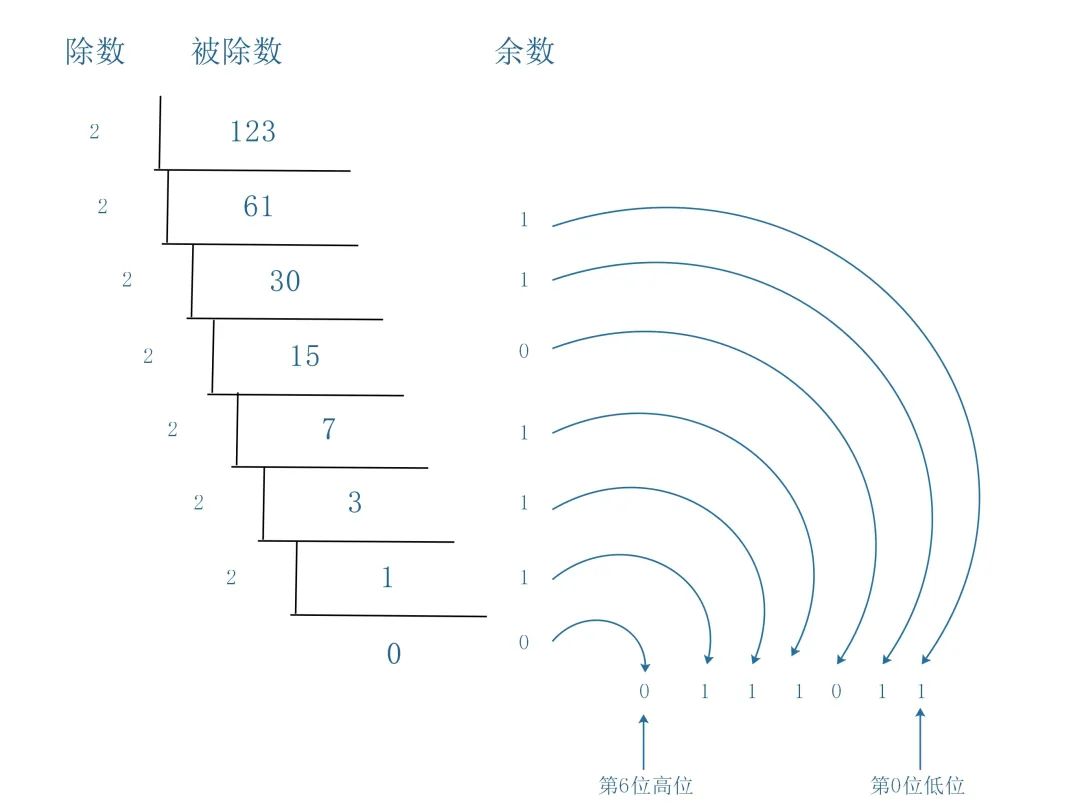 十进制转二进制
十进制转二进制
可以得到 123 的二进制表达为
0111011
。
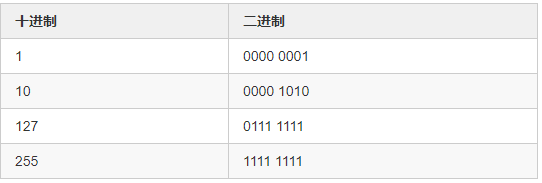
其他一些数的转换我也列在下面了:
但是在实际电路中,这样的编码设计起来
太复杂,
所以电路里面一般用下面的编码形式。
BCD 码
如果单纯为了
传输
而不需要对数字进行加减等处理的话,搞个四位对一位的编码最省力,很容易用一个四输入一输出的编码器电路实现,传过去之后再用译码器转成十进制就行了。
于是有了 BCD 码(
Binary-Code Decimal
),常用的 BCD 码有
8421BCD 码
,
余 3 BCD码
和
2421BCD 码
。通常采用 4 位二进制数表示一位十进制数中的 0~9 这 10 个数码,优点是
二进制和十进制之间的转换可以快速进行
,缺点就是
有 6 种状态为冗余状态
。
这里着重介绍一下
8421BCD 码
。
8421BCD 码是最基本和最常用的BCD码,它和四位自然二进制码相似,各位的权值为 8、4、2、1,故称为有权 BCD 码。
和四位自然二进制码不同的是,它只选用了四位二进制码中前 10 组代码,即用
0000~1001
分别代表它所对应的十进制数,余下的六组代码不用,便是 8421BCD 码的六种冗余状态。
让我们直接看表格吧,更直观一点
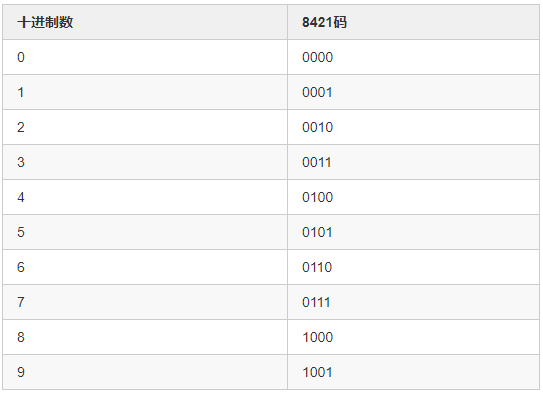
从表格里可以发现,0~9 的 8421BCD 码和自然二进制的前十个一模一样。
从 10 开始就有所不同了,举以下几个例子:
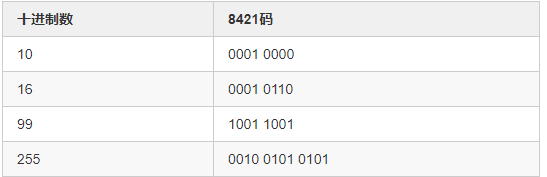
比如求 16 的 8421BBCD 码,先将 16 分开成 1 和 6 。
因为1 的二进制为 0001 ,6 的二进制为 0110,所以得到 0001 0110。
很显然,有多少位的十进制,就拆开成多少位,再对每一位进行单个编码。
实现基本逻辑门
在这一小节里,我们将开始借助
我的世界
里的物品实现简单的逻辑门,看下图片先熟悉一下这些物品:
 物品介绍
物品介绍
从左到右分别是:
好了,有了以上的基础,我们就可以来实现基本逻辑门了。
非门
非门有一个输入和一个输出端。当其输入端为高电平(逻辑 1 )时输出端为低电平(逻辑 0 ),当其输入端为低电平时输出端为高电平。
也就是说,输入端和输出端的
电平状态总是反相
的。非门的逻辑功能相当于逻辑代数中的非,电路功能相当于反相,这种运算亦称非运算。
逻辑图
当 A 端有输入信号时,Y 端不输出;
当 A 端无信号时,Y 端输出。
非门逻辑表达式为:
 非逻辑表达式
非逻辑表达式
逻辑图为:
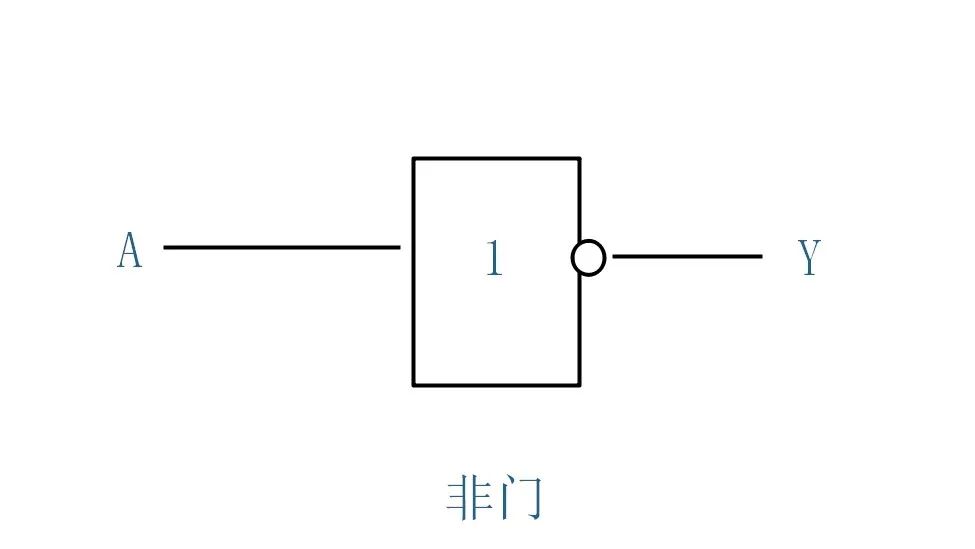 非逻辑图
非逻辑图
实现图
利用红石火把反转信号的特性,可快速实现一个非门。类比高低电平,游戏里的
激活
和
未激活
状态分别表示了
逻辑 1
和
逻辑 0
。
 非开
非开
 非关
非关
利用以上装置可以将输入的信号进行反相。
或门
或门有多个输入端,一个输出端,只要输入中有一个为高电平时(逻辑 1 ),输出就为高电平(逻辑 1 );只有当所有的输入全为低电平(逻辑 0 )时,输出才为低电平(逻辑 0 )。
逻辑图
当 A,B 端有一个输入信号时,Y 端就输出信号。只有当 A,B 都无信号时,Y 端不输出。
或门逻辑表达式为∶
Y=A+B
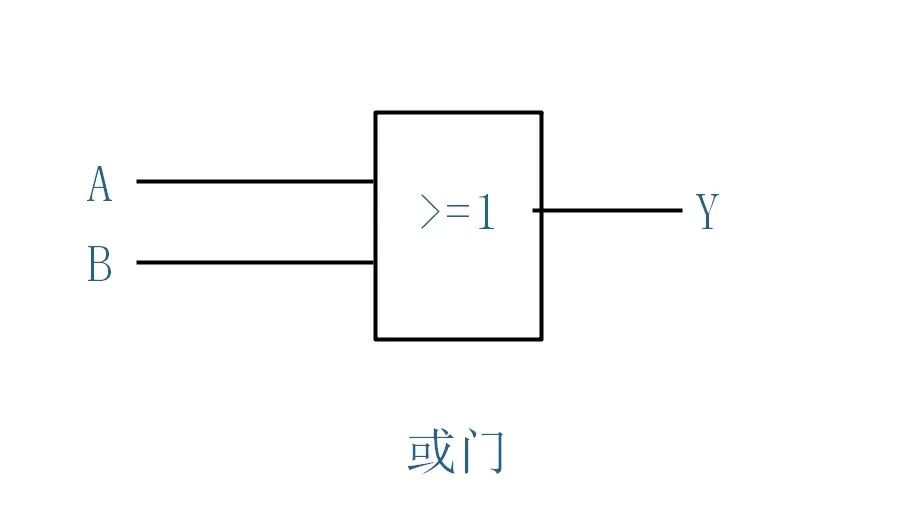 或逻辑图
或逻辑图
实现图
将两个输入端用红石电路并联在一起,可实现一个或门。
只有同时没有输入,输出才为 0 。
 或关
或关
只要有一个输入,输出就为 1 。
 或开
或开
与门
与门有多个输入端,一个输出端。当所有的输入同时为高电平(逻辑 1 )时,输出才为高电平,否则输出为低电平(逻辑 0 )。
逻辑图
当 A,B 端同时输入信号时,Y 端才输出信号。A,B 有一个无信号时,Y 端不输出。
与门逻辑表达式为∶
Y=AB
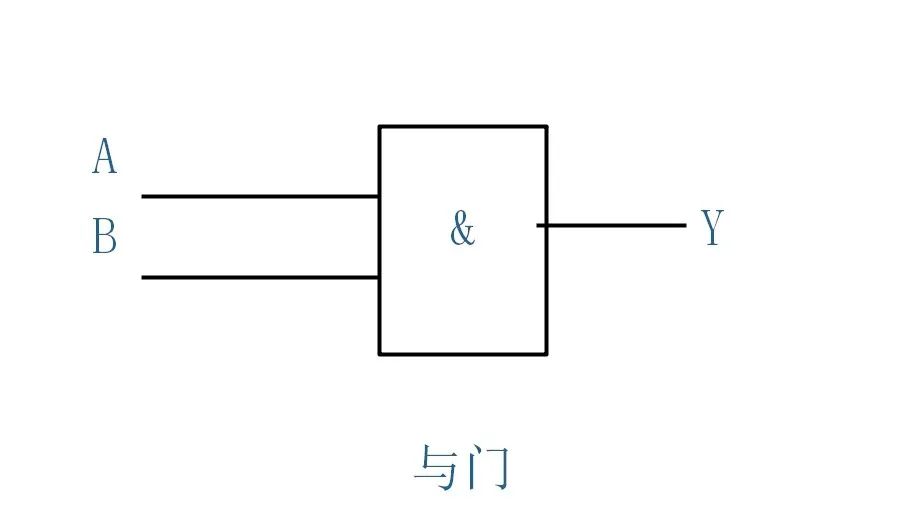 与逻辑图
与逻辑图
实现图
与门作为一个基本的逻辑门电路,可是在我的世界里面没有现成的电路来表示与门。
但是我们往上翻,会发现我们已经实现完了或门和非门。此时可以用
摩根定律
来求出与门的等价逻辑表达式:
 摩根定律
摩根定律
即两个输入端各搭非门,合并信号后再加个非门。
如下图所示,只有当两个输入端都有信号时,输出端才输出。
 与非
与非
只有一个输入信号则不输出。
 与关
与关
可能你会有点意外,
这样还能叫与门吗
?
其实无论在电路组成上采用什么形式,
只要最后的结果是一个与逻辑
,那么
它就是与门,
即使通过与非门和非门组合而成,它也叫做"与门"而不叫"与非非"门。
简单来说,你去买一个电路的时候,也只会关心它的输入与输出间的逻辑关系最终是什么。
至此,与、或、非已全部实现,且组成完备集,可以表达所有电路。
但是在实际应用中,我们不得不提到下面这个逻辑门——与非门。
与非门
在集成电路中,
与非门
和
或非门
是仅次于
非门
的第二简单的门,但
与非门
比
或非门
性能好,而且用
与非门
可以
实现任意逻辑表达式
。这么高的性价比,与非门确实是有资格作为表达式的终极化简因子的。
在手工设计电路时,如果可以的话,工程师是倾向于用与非门的,后续我们设计电路时,也倾向于
把表达式转换为与非门
。
逻辑图
当 A,B 端同时输入信号时,Y 端才不输出信号。其他情况时,Y 端都输出。
与非门逻辑表达式为∶
 与非逻辑表达式
与非逻辑表达式
逻辑图为:
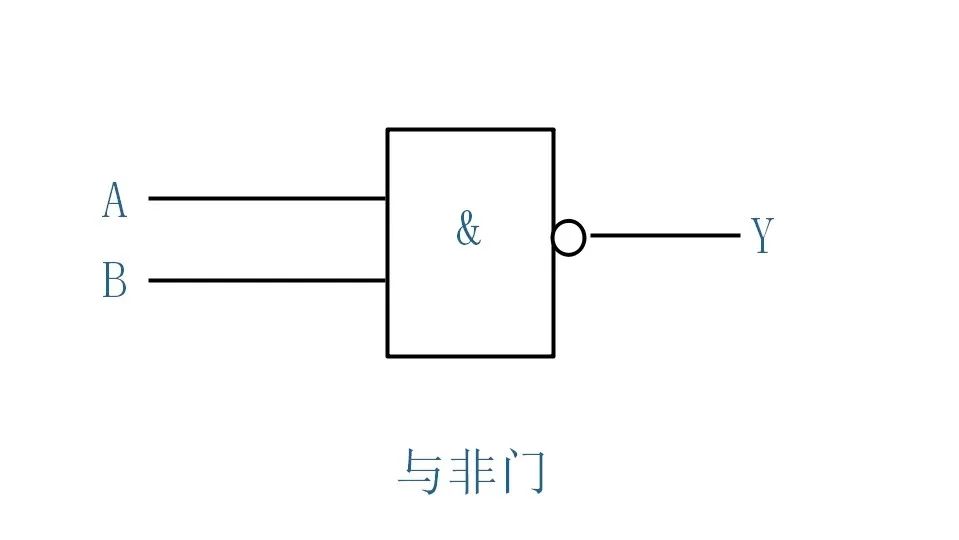 与逻辑图
与逻辑图
实现图
我们将与门表达式代入以上表达式,并计算
 与非表达式化简
与非表达式化简
发现消掉了与门的最后一个非门,与非门实现了对与门的化简,只要两个输入端各搭一个非门,将输出并联在一起就能实现。
这也是我在设计电路时,倾向于
把表达式化简为与非门
的原因之一。
 与非
与非
组合电路
当然,只有逻辑门还是不够的,接下来我们将在这些基本逻辑门的基础上来实现一些复杂的组合电路,最后再连接起来。
为了不被复杂的电路套进去,专注于原理,我对显示器进行了化简,功能为可以选择将 0、1、2、3 这四个数输出在显示器上。
编码器
由前面所介绍的知识可知,十进制在电路里是按 8421BCD 码进行传输的。那我们要怎么将十进制码转换为 8421BCD 码呢?这就是编码器要做的事了。
我们的显示器可以选择四个数显示,所以编码器只要将 0~3 进行编码即可。
编码器的输入端要有四个,分别是 I₀、I₁ 、I₂ 和 I₃,输出端为 Y₀ 和 Y₁。
如果要对 2 进行编码,则将 I₂ 输入信号,其他输入端无信号,为 0。对应的输出端为 10,这个 10 就是 2 的 BCD 码。
对其他数编码同理,完整的功能表如下,输入端 I 为 1 时,表示对应的数被按下:
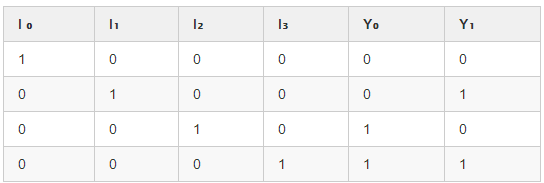
根据功能表写出输出逻辑函数表达式:
将表达式变换为与非表达式:
 编码器逻辑表达式
编码器逻辑表达式
根据以上与非表达式可画出逻辑图。
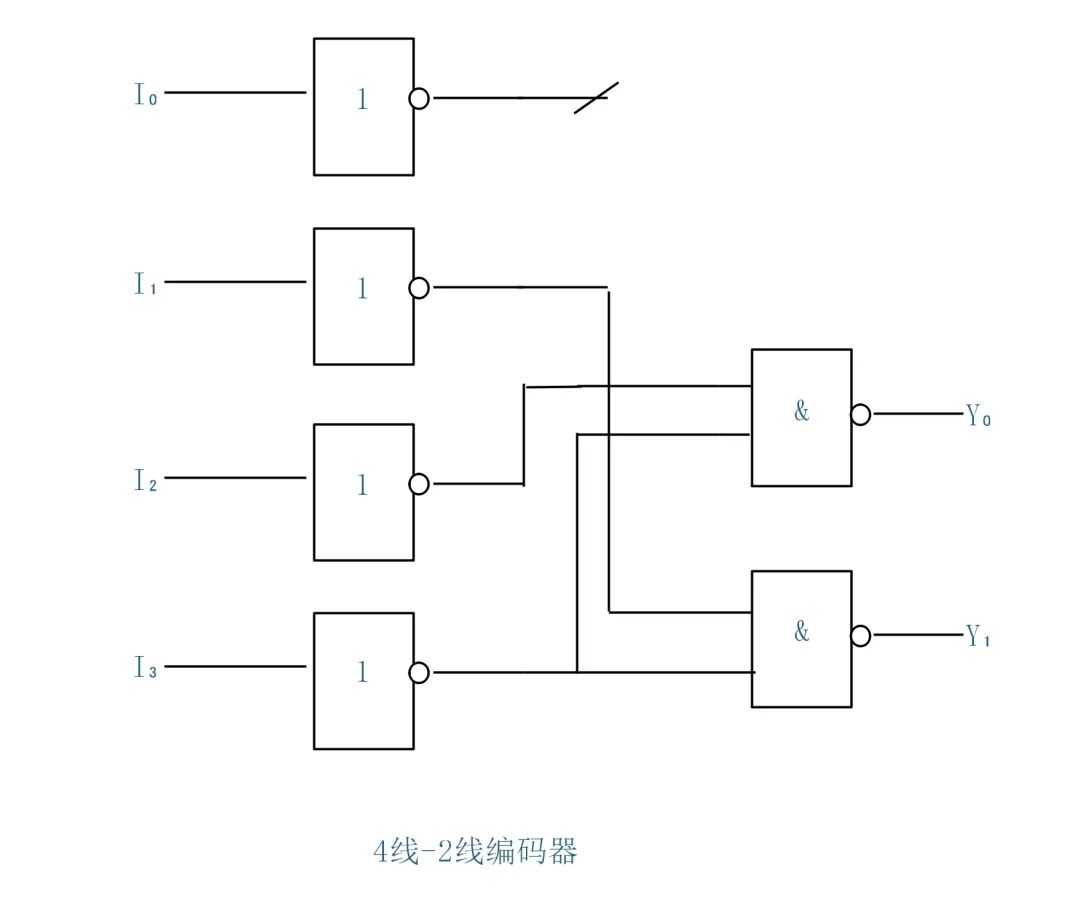 编码器逻辑图
编码器逻辑图
即输入端各搭非门,按逻辑表达式加与非门。
实现图
这是我们的五个输入端,第一个消隐端/总开关将在下面的小节进行讲解,后面四个就是我们可以选择的数字。
 编码器输入
编码器输入
从上面俯瞰一下,电路从这五个输入端引出。
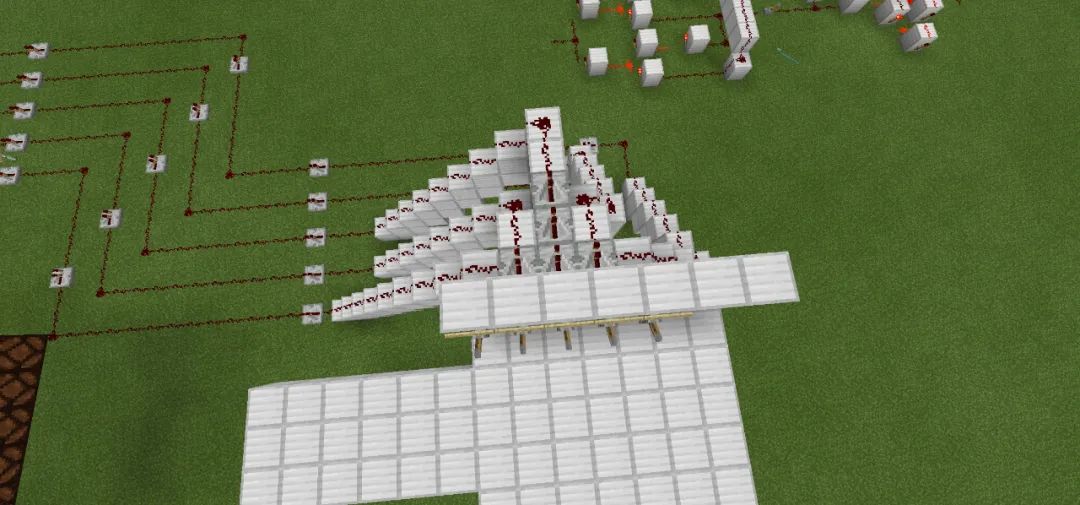 编码器俯视图
编码器俯视图
这是编码器的具体实现部分:
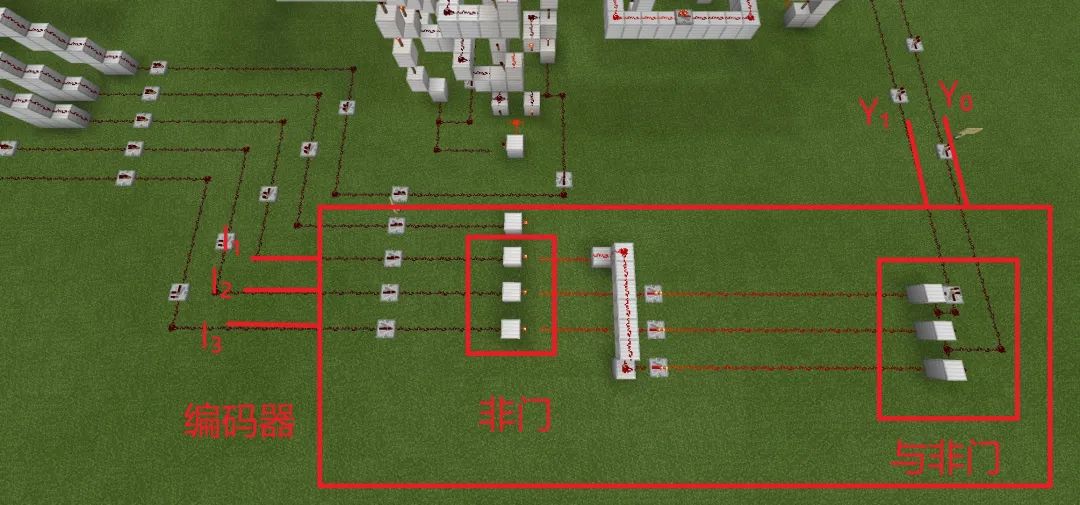 编码器实现部分
编码器实现部分
应当指出,当 I₀ ~ I₃ 都为 0 时,输出 Y₀Y₁=00,所以 I₀ 输入线可以
不接入编码器
。


















