查看历史文章,请点击上方链接关注公众号。
上节
我们介绍了ConcurrentHashMap,其中提到HashMap可能会出现死循环,但并未解释原因,有读者提问,我们稍微解释下。
死循环出现在多个线程同时扩容哈希表的时候
,不是同时更新一个链表的时候,那种情况可能会出现更新丢失,但不会死循环,具体过程比较复杂,我们就不解释了,感兴趣的读者可以参考这篇文章,http://coolshell.cn/articles/9606.html。
ConcurrentHashMap不能排序,容器类中可以排序的Map和Set是
TreeMap
和
TreeSet
,但它们不是线程安全的。Java并发包中与TreeMap/TreeSet对应的并发版本是ConcurrentSkipListMap和ConcurrentSkipListSet,本节,我们就来简要探讨这两个类。
基本概念
我们知道,TreeSet是基于TreeMap实现的,与此类似,ConcurrentSkipListSet也是基于ConcurrentSkipListMap实现的,所以,我们主要来探讨ConcurrentSkipListMap。
ConcurrentSkipListMap是基于SkipList实现的,SkipList称为跳跃表或跳表,是一种数据结构,待会我们会进一步介绍。并发版本为什么采用跳表而不是树呢?原因也很简单,因为跳表更易于实现高效并发算法。
ConcurrentSkipListMap有如下特点:
-
没有使用锁,
所有操作都是无阻塞的,所有操作都可以并行,包括写
,多个线程可以同时写。
-
与ConcurrentHashMap类似,迭代器不会抛出ConcurrentModificationException,是弱一致的,迭代可能反映最新修改也可能不反映,一些方法如putAll, clear不是原子的。
-
与ConcurrentHashMap类似,同样实现了ConcurrentMap接口,直接支持一些原子复合操作。
-
与TreeMap一样,可排序,默认按键自然有序,可以传递比较器自定义排序,实现了SortedMap和NavigableMap接口。
看段简单的使用代码:
public static void main(String[] args) {
Map
map = new
ConcurrentSkipListMap(
Collections.reverseOrder()
);
map.put("a", "abstract");
map.put("c", "call");
map.put("b", "basic");
System.out.println(map.toString());
}
程序输出为:
{c=call, b=basic, a=abstract}
表示是有序的。
ConcurrentSkipListMap的大部分方法,我们之前都有介绍过,有序的方法,与TreeMap是类似的,原子复合操作,与ConcurrentHashMap是类似的,所以我们就不赘述了。
需要说明一下的是它的size方法,与大多数容器实现不同,这个方法不是常量操作,它需要遍历所有元素,复杂度为O(N),而且遍历结束后,元素个数可能已经变了,一般而言,在并发应用中,这个方法用处不大。
下面我们主要介绍下其基本实现原理。
基本实现原理
我们先来介绍下跳表的结构,
跳表是基于链表的,在链表的基础上加了多层索引结构
。我们通过一个简单的例子来看下,假定容器中包含如下元素:
3, 6, 7, 9, 12, 17, 19, 21, 25, 26
对Map来说,这些值可以视为键。ConcurrentSkipListMap会构造类似下图所示的跳表结构:
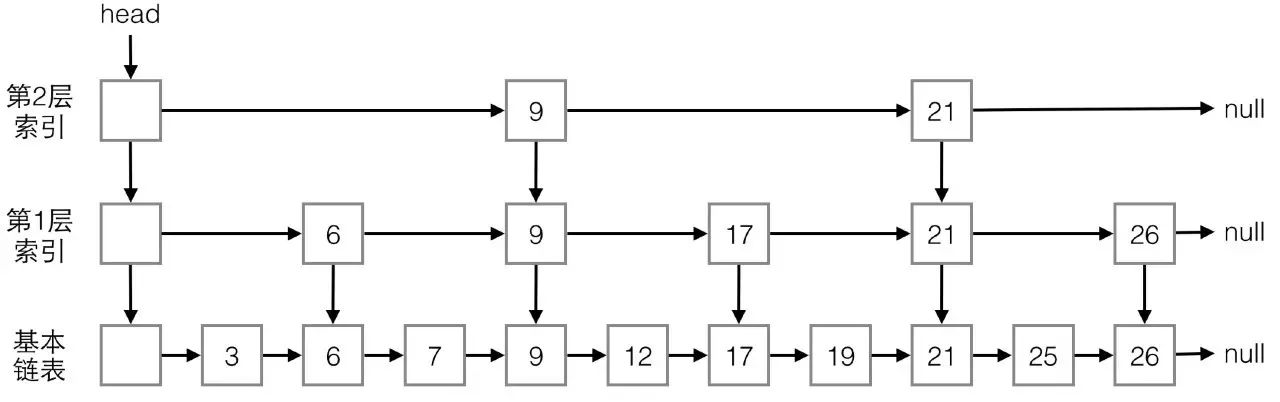
最下面一层,就是最基本的单向链表,这个链表是有序的。虽然是有序的,但我们知道,与数组不同,链表不能根据索引直接定位,不能进行二分查找。
为了快速查找,跳表有多层索引结构,这个例子中有两层,第一层有5个节点,第二层有2个节点。
高层的索引节点一定同时是低层的索引节点
,比如9和21。
高层的索引节点少,低层的多,统计概率上,第一层索引节点是实际元素数的1/2,第二层是第一层的1/2,逐层减半,但这不是绝对的,有随机性,只是大概如此。
对于每个索引节点,有两个指针,一个向右,指向下一个同层的索引节点,另一个向下,指向下一层的索引节点或基本链表节点。
有了这个结构,就可以实现类似二分查找了
,查找元素总是从最高层开始,将待查值与下一个索引节点的值进行比较,如果大于索引节点,就向右移动,继续比较,如果小于,则向下移动到下一层进行比较。
下图两条线展示了查找值19和8的过程:
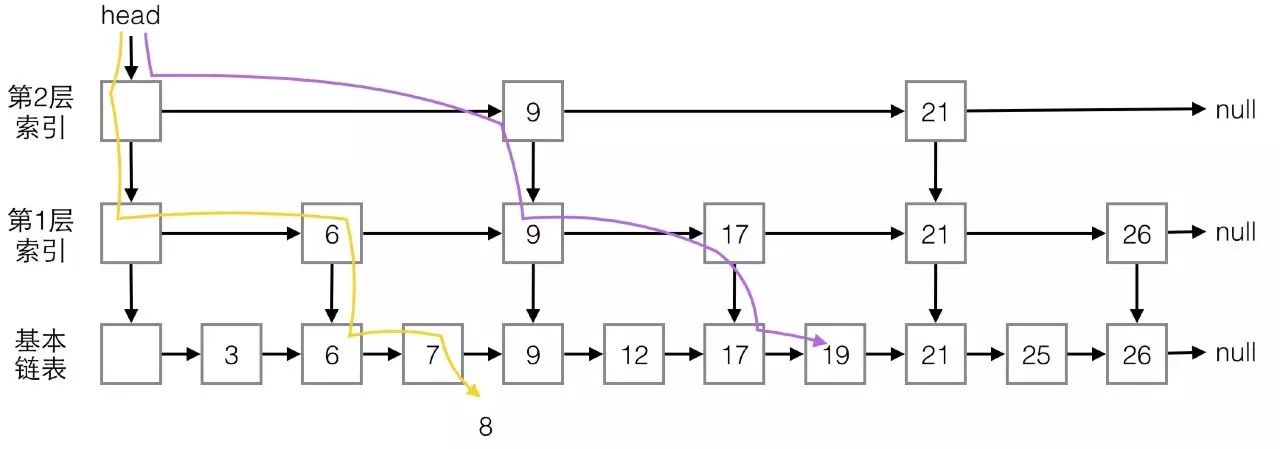
对于19,查找过程是:
-
与9相比,大于9
-
向右与21相比,小于21
-
向下与17相比,大于17
-
向右与21相比,小于21
-
向下与19相比,找到
对于8,查找过程是:
-
与9相比,小于9
-
向下与6相比,大于6
-
向右与9相比,小于9
-
向下与7相比,大于7
-
向右与9相比,小于9,不能再向下,没找到
这个结构是有序的,查找的性能与二叉树类似,复杂度是O(log(N)),不过,这个结构是如何构建起来的呢?
与二叉树类似,这个结构是在更新过程中进行保持的,保存元素的基本思路是:
-
先保存到基本链表,找到待插入的位置,找到位置后,先插入基本链表















