这次学习会讲了隐马尔科夫链，这是一个特别常见的模型，在
自然语言处理
中的应用也非常多。
常见的应用比如
分词，词性标注，命名实体识别等问题序列标注问题
均可使用隐马尔科夫模型.
下面，我根据自己的理解举例进行讲解一下HMM的基本模型以及三个基本问题，希望对大家理解有帮助~
隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程。
隐藏的马尔可夫链随机生成的状态的序列，称为状态序列（state sequence);每个状态生成一个观测，而由此产生的观测的随机序列，称为观测序列（observation sequence)。
序列的每一个位置又可以看作是一个时刻。
下面我们引入一些符号来表示这些定义：
设Q是所有可能的状态的集合，V是所有可能的观测的集合。
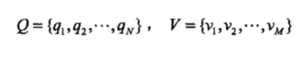
其中，N是可能的状态数，M是可能的观测数。
状态q是不可见的，观测v是可见的。
应用到
词性标注
中，v代表词语，是可以观察到的。q代表我们要预测的词性（一个词可能对应多个词性）是隐含状态。
应用到
分词
中，v代表词语，是可以观察的。q代表我们的标签（B,E这些标签，代表一个词语的开始，或者中间等等）
应用到
命名实体识别
中，v代表词语，是可以观察的。q代表我们的标签（标签代表着地点词，时间词这些）
上面提到的方法，有兴趣的同学可以再细入查阅相应资料。
I是长度为T的状态序列，O是对应的观测序列。
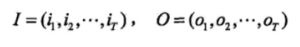
我们可以看做是给定了一个词（O）+词性（I）的训练集。
或者一个词(O)+分词标签（I）的训练集....有了训练数据，
那么再加上训练算法则很多问题也就可以解决了
，问题后面慢慢道来~
我们继续定义A为状态转移概率矩阵：
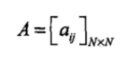
其中，
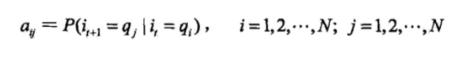
是在时刻t处于状态qi的条件下在时刻t+1转移到状态qj的概率。
B是观测概率矩阵:
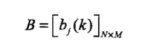
其中，
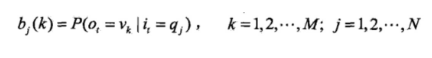
是在时刻t处于状态qj的条件下生成观测vk的概率（
也就是所谓的“发射概率”
）。
所以我们在其它资料中，常见到的生成概率与发射概率其实是一个概念。
π是初始状态概率向量：
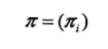
其中，
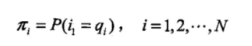
隐马尔可夫模型由初始状态概率向量π、状态转移概率矩阵A和观测概率矩阵B决定。π和A决定状态序列，B决定观测序列。因此，隐马尔可夫模型可以用三元符号表示，即
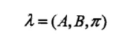
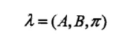称为隐马尔可夫模型的三要素。
如果加上一个具体的状态集合Q和观测序列V，构成了HMM的五元组，这也是隐马尔科夫模型的所有组成部分。
举例来说明一下，例子如下：（例子来源于维基百科）
考虑一个村庄，所有村民都健康或发烧，只有村民医生才能确定每个人是否发烧。医生通过询问患者的感受来诊断发烧。村民只能回答说他们觉得正常，头晕或感冒。（
这里的正常，头晕，感冒就是我们前面说的观察序列
）
医生认为，他的患者的健康状况作为离散的马可夫链。 “健康”和“发烧”有两个状态，但医生不能直接观察他们;健康与发烧的状态是隐藏的（这
里的健康与发烧就是我们前面说的隐藏状态
）。每天都有机会根据患者的健康状况，病人会告诉医生他/她是“正常”，“感冒”还是“头昏眼花”。
观察（正常，感冒，晕眩）以及隐藏的状态（健康，发烧）形成隐马尔可夫模型（HMM），并可以用Python编程语言表示如下：
在这段代码中，start_probability代表了医生对患者首次访问时HMM所处的状态的信念（他知道患者往往是健康的）。
这里使用的特定概率分布不是平衡的，它是（给定转移概率）大约{'健康'：0.57，'发烧'：0.43}。（
这里代表的就是我们前面说的初始状态概率pi
