为何五次方程没有求根公式？

引言：大家都知道，一元一次、二次、三次、四次方程都有根式解，从五次方程开始就没有一般解了。然而这个情况为什么是五次方程开始出现？为什么这个数字是五？为什么不是六或者是七？为什么恰好是五次方程才开始没有根式解？难道说当多项式的次数达到五的时候，其形态会有根本性的改变？

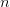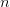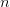另外，就是现行初中数学教材关于一元二次方程的章节中，专门会提到「 配方法 」，包括推导一元二次方程的求根公式时也用到了它。然而，这种方法 只对二次方程有效，二次以上的多项式在配 次方之后并不能总保证在「完全 次方项」之后仅有常数项 （见图）。实际上， 对于任意一个多项式，我们总可以只借助最高项和次高项，根据二项式定理，凑出「完全 次方项」。

以配立方为例：

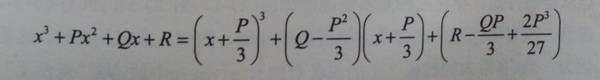
具体过程如下 ：

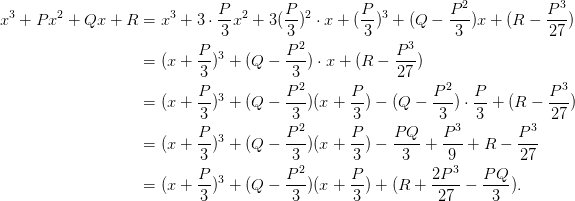
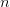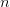个人觉得， 配方法在某种程度上具有误导性。这种方法很容易使人误以为：解一元 次多项式方程，只需将带有 的项都移到等号的一侧，然后配 次方，再开 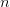次方即可。

有一次 Dror Bar-Natan 来卡内基梅隆大学给本科生讲座，我导师居然去听了，并且他也推荐我去。从那次讲座以后，我终于可以绕开抽象代数理论（域扩张、Galois 理论等等），向一个 仅接触过复数的路人 解释 Abel–Ruffini 定理了，即「为何五次方程没有求根公式」。如果你会编程，那还可以额外享受自行验证部分证明的乐趣。要知道，对于一般的本科教学，经过一学期群环域的轮番折磨，学生才可能在学期末触及 Abel–Ruffini 定理这个巅峰。

插播一则轶事，Dror Bar-Natan 在加拿大入籍的时候，发现需要宣誓：

I affirm that I will be faithful and bear true allegiance to Her Majesty Queen Elizabeth II, Queen of Canada, Her Heirs and Successors, and that I will faithfully observe the laws of Canada and fulfill my duties as a Canadian citizen.

他表示很乐意遵守法律、履行加拿大公民义务……但是向女王或者她的子嗣效忠？老子不干！于是 2012 年他和小伙伴组队上加拿大最高法院讲理去了。很不幸 2015 年最高法院驳回了上诉。最后，他和小伙伴在宣誓加入加拿大籍后公开否认誓言的前半部分。

言归正传，首先要明确「当我们在谈论求根公式时我们在谈论什么」。例如，求根公式 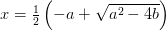给出任何二次方程 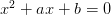的一个根。所以，五次方程求根公式（如果存在的话）应当

1. 给出任何五次方程 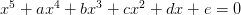的一个根；

2. 并且是一个关于 a, b, c, d, e 且仅含加减乘除开方的代数表达式。

对于特定类型的五次方程，如 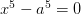，虽然有一个仅含加减乘除开方的解 x = a， 但这并不是我们要谈论的求根公式。

接下来的 Abel–Ruffini 定理的证明是基于 Vladimir Arnold 在 1963 年的拓扑证明（开启了拓扑 Galois 理论）。其他回答中最接近的应该是韩京俊的解答，我的回答将牺牲一小部分严谨性来换取可读性。

这个证明需要一位假想敌（想象一位你最希望打脸的朋友），他或她宣称拥有五次方程求根公式 x = f ( a, b, c, d, e )（随便写的复杂公式，不要在意细节）：

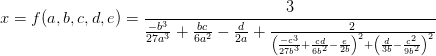
我们按照如下计划去推翻这个公式：

1. 随意选取五个复数 x1, …, x5 并构造五次方程 使得其根恰是 x1, …, x5 ；

2. 将五次方程的系数 a, b, c, d, e 代入假想敌提供的公式中算出 x = f ( a, b, c, d, e ) 并展示 x 不在 x1, …, x5 中。

计划的第一步，在选定 x1, …, x5 后，可以通过展开 ( x - x1 )( x - x2 )( x - x3 )( x - x4 )( x - x5 ) = 0得到想要的五次方程的系数，例如： a = - ( x1 + x2 + x3 + x4 + x5 ) , …, e = - x1 x2 x3 x4 x5 。具体的系数与根之间的关系就是大家初中学的 Vieta 公式（韦达定理）。计划的第二步只需要机械式地代入计算 x 并比对 x1, …, x5 即可。

然而，这个计划并不一劳永逸——每次假想敌宣称有新的五次方程求根公式，我们都需要重新执行上面描述的计划去推翻。

升级版计划 是让 x1, …, x5 动起来！想象如下运动：同时地， x1 向 x2 移动， x2 向 x3 移动， x3 向 x4 移动， x4 向 x5 移动。在运动的同时，我们

1. 不断用 Vieta 公式计算系数 a, b, c, d, e 的值，

2. 再不断代入 f ( a, b, c, d, e ) 计算 x 的值。

为方便起见，我们用数组 P = (2, 3, 4, 5, 1) 来表示所描述的运动，一般地，数组从左到右依次记录了 x1, …, x5 运动终点 x 的下标。这样让 x1, …, x5 交换位置的运动，我们称为 置换 Permutation 。

因为整个运动只是将 x1, …, x5 换了换位置且 Vieta 公式关于 x1, …, x5 都是对称的，所以在运动后， a, b, c, d, e 都回到了起始的位置。示意图如下：

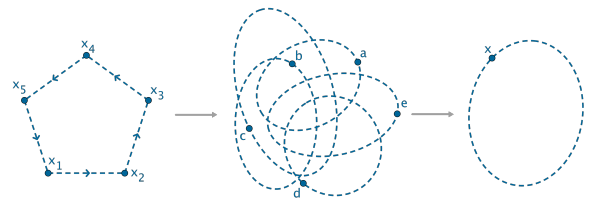
由于 f 在运动前后都代入了同样的 a, b, c, d, e ，于是 x = f ( a, b, c, d, e ) 应当回到它起始的位置！慢着，如果 x 在运动开始前是 x1, …, x5 中的某个，不妨设是 x1 ，那么在连续运动的过程中 x 应该一直和 x1 保持一致，并在运动后落在原本 x2 的位置上。打脸成功！

细心的读者会反问：上面的证明压根没用到 5 次方程这个条件，那岂不是可以证明任何方程都没有求根公式了？我们读的一定是假的证明……

确实，以上论证存在缺陷——在计算 x = f ( a, b, c, d, e ) 的时候，忽视了公式含有开方的可能。

为了说明这个缺陷，我们将以上的论证应用在 2 次方程 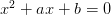和求根公式 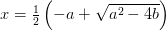上。第一步，Vieta 公式告诉我们 a = - ( x1 + x2 ), b = x1 x2 ；第二步中，先代入 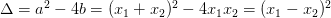，再开根得到 x1 - x2 或 x2 - x1 。想象将 x1 和 x2 互换的运动，虽然 Δ 会回到起始的位置，但是 √Δ 为了保证运动的连续性必须盯住 x1 - x2 或盯住 x2 - x1 ，于是在 x1 和 x2 互换后 √Δ 变成了自己的相反数。换个角度看，当 x1 和 x2 互换时， Δ 绕原点转了 1 圈，于是 √Δ 只绕了 1 / 2 圈。

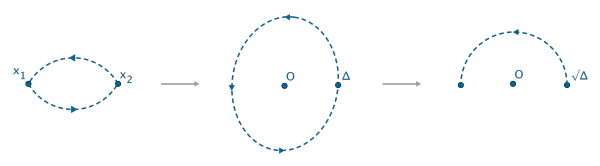
一般情况下，当复数 z 绕原点 k1 圈回到起始位置时， z 的 k 次根只绕了 k1 / k 圈。

因此，回到 5 次方程的情况，如果 f ( a, b, c, d, e )包含开方，那么升级版计划就不能保证 x 还能回到起始位置。当然，升级版计划是可以说明不出现开方的公式（例如那个复杂的随便写的公式）一定不是求根公式。这从一个侧面回答了「为何二至四次方程的求根公式里面必须出现开方」。

终极版计划 将延续升级版的思路：合理制定 x1, …, x5 的移动路径，使得

1. 根 x1 不回到自己原来的位置；

2. 系数 a, b, c, d, e 在某种意义上绕原点圈数（以下简称 绕数 winding number ）为 0。

为此，我们需要引入置换的 复合 Composition 逆 Inverse 交换子 Commutator 三个概念。

两个置换的复合，就是将两个置换运动的录像连着播放：

置换的逆，就是把一个置换运动的录像倒着播放：

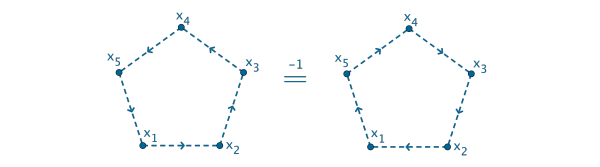
两个置换 P1, P2 的交换子定义为 。可以把交换子 [ P1, P2 ] 分解为如下 4 个过程：

1. 先播放置换运动 P1 的录像；

2. 连着播放置换运动 P2 的录像；

3. 再倒放置换运动 P1 的录像；

4. 最后倒放置换运动 P2 的录像。

如果假想敌宣称求根公式是 ，其中 A, B 是 a, b, c, d, e 的只含加减乘除的代数式。考虑在置换 P = [ P1, P2 ] 的作用下 A 的运动：在过程 1, 2 中假设 A 的绕数分别是 k1, k2 ，则在过程 3, 4 中倒放录像 A 的绕数分别是 -k1, -k2 ，于是 A 总绕数为 0，故 回到起始位置。同理， 也回到起始位置。综上， x 将回到起始位置。

如果假想敌宣称求根公式是 ，其中 A, B, C, D 是 a, b, c, d, e 的只含加减乘除的代数式。令 P = [ P1, P2 ] , P1 = [ P3, P4 ] , P2 = [ P5, P6 ]，也就是说 P = [ [ P3, P4 ], [ P5, P6 ] ]。因为 P1 = [ P3, P4 ] 是交换子，我们知道 在 P1 作用下回到起始位置，于是 在 P1 作用下回到起始位置；同理 在 P2 作用下也回到起始位置。由于 P = [ P1, P2 ] 是交换子，故 在 P 的作用下回到起始位置。以此类推，可得 x 将回到起始位置。

可以看出交换子的交换子可以处理两层开方的情形。一般地，交换子的交换子的……的交换子（默念 m 遍交换子）可以处理有 m 层开方的情形。

为了满足「根 x1 不回到自己原来的位置」这个条件，剩下的任务就是找到一个既移动 x1 又能表示成「交换子的交换子的……的交换子」的置换。记所有置换构成的集合为 S5 ，又记所有交换子，即 [ P1, P2 ]（其中 P1, P2 来自 S5 ），构成的集合为 A5 。下面的 Ruby 程序将计算 A5 和交换子的交换子构成的集合。

require 'set'def compose(p1, p2)
  (1..5).map { |i| p2[p1[i - 1] - 1] }enddef invert(p)
  (1..5).map { |i| p.index(i) + 1 }enddef commutate(p1, p2)
  compose(compose(compose(p1, p2), invert(p1)), invert(p2))ends5 = Set.new (1..5).to_a.permutation.to_aputs "#{s5.length} permutations: #{s5.inspect}"a5 = Set.newfor p1 in s5
  for p2 in s5
    a5 << commutate(p1, p2)
  endendputs "#{a5.length} commutators: #{a5.inspect}"commutators_of_a5 = Set.newfor p1 in a5
  for p2 in a5
    commutators_of_a5 << commutate(p1, p2)
  endendputs "#{commutators_of_a5.length} commutators of commutators: #{commutators_of_a5.inspect}"

输出：

120 permutations: #60 commutators: #60 commutators of commutators: #

我们发现，交换子的交换子构成的集合与 A5 一模一样！也就是说，任取一个 A5 中的元素 P ，比如说 P = (3, 2, 1, 5, 4) 将 x1 移动至 x3 ，都可以在 A5 中找到 P1, P2 使得 P = [ P1, P2 ]，于是又能在 A5 中找到 P3, P4, P5, P6 使得 P1 = [ P3, P4 ], P2 = [ P5, P6 ]，以此类推，子子孙孙无穷匮也，这样就完成了最终的任务。

附产品 1 ：考虑 1, 2, 3 间所有的置换、它们的交换子以及交换子的交换子，类似的程序输出

6 permutations: #3 commutators: #1 commutators of commutators: #

这说明三次方程求根公式一层开方是不够的，至少需要两层开方。

附产品 2 ：考虑 1, 2, 3, 4 间所有的置换、它们的交换子、交换子的交换子、交换子的交换子的交换子，类似的程序输出

24 permutations: #12 commutators: #4 commutators of commutators: #1 commutators of commutators of commutators: #

这说明四次方程求根公式两层开方是不够的，至少需要三层开方。

最后，致修炼数学的读者，抽象代数还是要好好学的。

高质量延伸阅读

☞ 第一个被认为“科学家”的人:泰勒斯