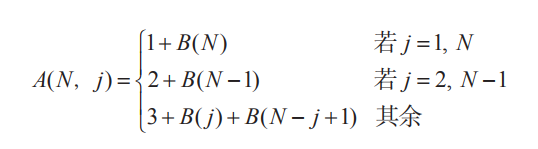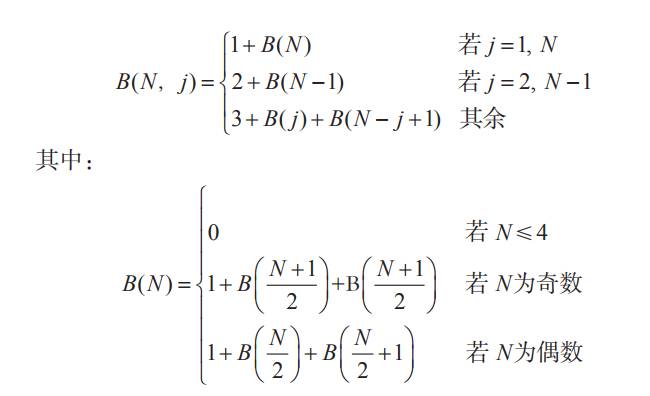“你都喝了三杯啤酒了,就不想……”
“做数学?”
***
数学家喜欢研究十分重要的问题,比如非局部扩散算子第一特征值的上下界。数学家也会研究十分困难的问题,比如有限谱算子舒尔-霍恩定理。但如果厌倦了这些抽象又困难的领域,他们也会研究一些无关紧要的问题。
加拿大卡尔顿大学的信息科学家埃万耶洛斯·克拉纳基斯和美国卫斯理大学的数学家丹尼·克里赞克便是如此。2010年,他们共同署名发表了关于随机共线传感器最大干扰的文章。之后,二人决定放松一下,研究一个不那么棘手的问题:如厕时怎么选择小便池。
两位学者以最严肃的科研精神,发挥聪明才智写成一篇12页的论文,题为《小便器问题》(The Urinal Problem)。问题如下:有一排小便器,如果如厕者不想被打扰,选哪一个最好?高德纳曾用组合法计算过斯坦福大学信息科学系应该多久换一次厕纸。两人看到高德纳的研究结果后十分开心,这才有了“小便器优选法”的研究。

图20.1,21个小便器,1个最佳选择……哪个?
重要问题要说得具体。酒吧气氛正浓,你已喝了3杯啤酒,膀胱告急。酒吧的厕所特别大,而且神奇的是一个人都没有。这是个典型的男厕所,方形屋子,进去后左边是一排N个小便器,右边是隔间和洗手池。你(下文中的“你”指站着小便的人。如果不符合你的情况,可默默将“小便器”替换成“椅子”,将“厕所”替换成“候诊室”。问题实质不变,只是没那么好笑。)是第一个内急来上厕所的人,但门外已有一群啤酒爱好者在吵吵嚷嚷。不巧的是,隔间的门刚刷过漆,现在用不了。既然是来方便嘛,就要尽量“方便”,也就是说,最好不要有人站旁边。假设小便器都一样干净,任君选择,选哪个才能酣畅淋漓呢?
直觉上,离门最远的小便器应该最好。如果下一个进来的“猛男”也只想安静地撒泡尿,他也会选个离你比较远的小便器,二人相安无事地尿完。但解答还得靠数学建模!一切都看后来者怎么选。模型有许多,但总原则不变——大家都想旁边没人。因此,除非不得已,不会有人挨着别人站。如果必须挨着,此时厕所即“饱和”。不“饱和”时,至少应该有1个小便器,两边都没人,即为“孤立”;如果仅一边有人,称为“半孤立”。因为你第一个进来,你的选择至关重要:要尽量扩大饱和所需的人数!
模型一:人性本懒
根据来此宝地后的选择,可以有好几种数学模型,第一种是“懒人模型”。位置总数很重要,假设进来的人自动选择离门最近的孤立小便器,在此假设下,可有两种情况:一种是小便器总数N为偶数,此时,饱和状态即1/2的小便器被占用。而此时不管你怎么选择小便器(位于奇数位或偶数位),饱和所需人数不受影响(图20.2)。如果小便器总数N为奇数,那么你应该选奇数位的小便器,(N+1)/2个小便器被占用时,厕所才会饱和,而不是(N-1)/2。
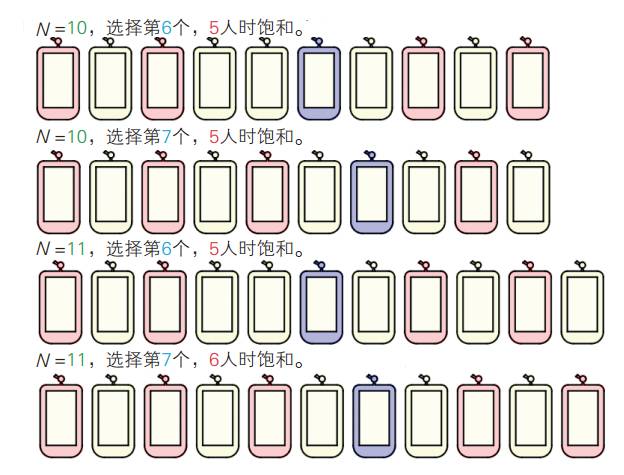
图20.2 小便器总数与饱和所需人数的关系
N为偶数时,你可以随意选择,饱和所需人数一样。比如,N=10时,不管选择第6个或第7个(蓝紫色),都要再有4人(粉红色)才饱和。另外要注意的是,如果选择第6个,则第4个和第5个半孤立,第6人进来应会选择二者之一。N为奇数时,应选奇数位小便器。比如一共有11个位置时,假如选择第7个的话,则还可容纳5人,选择第6个,就只能再容纳4人。
就算厕所饱和了,人不能给尿憋死。这时又该怎么办?克拉纳基斯和克里赞克在文中设想了两种情景。
第一种,新来的人依旧遵守懒人原则,即使小便器非孤立,依旧就近选择。这时,你选择离门越远的位置越好。假设新来的人会优先选择半孤立小便器,结论也一样。实际上,如果你左手边的两个位置都没人,按照懒人模型,后来者更爱选择更靠左的那个便池。注意,此时你不应该选倒数第二个位置,因为饱和时,你右边的位置半孤立,很容易有人选。
第二种更有可能发生,在没有孤立位置之后,新来的人随机选择,剩下的位置被选中的概率均等。此时你应该选择两端的位置,因为仅一边有人,感觉稍微好一点吧。
总之,离门越远越好。
让我们用方程总结一下。设第一人走进厕所时为t = 1,之后依次为t = 2, 3, 4,等等。如果N为偶数,则t=N/2时饱和;如果N为奇数,若第一人选择了奇数位,则t=(N+1)/2时饱和,若第一人选择偶数位,则t=(N-1)/2时饱和。
厕所饱和之后,新来的人随机选择。如果你选了两端的位置,旁边来人的平均加数[2]为(N+2)/4(其中N为偶数),或者(N+1)/4(其中N为奇数)。
[2]这一平均加数符合负超几何分布。可以证明,此分布的预期值为(n+1)(a+1),其中n表示剩余的位置,在不同情况下分别为N/2、(N+1)/2或(N-1)/2,而a表示相邻位置的数量,对于两端的位置a=1,对于其他位置a=2。
如果你开始选择了其他位置,则旁边来人的平均加数为(N+2)/6(图20.3)。
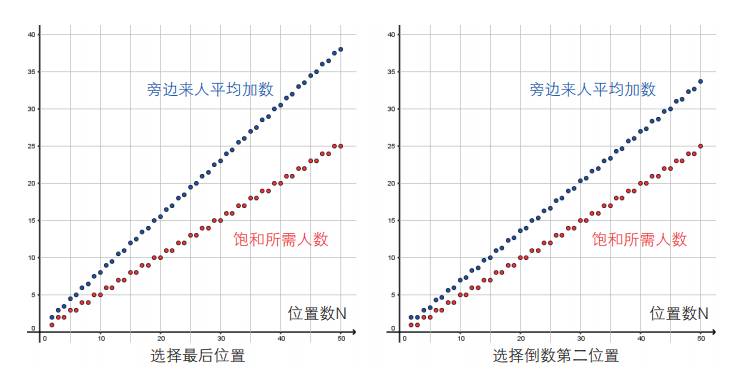
图20.3 计算结果很清楚,不管总共有多少位置,离门越远的位置,旁边越不易有人
模型二:人性本羞
按照第一种模型,就算厕所很大,人也会聚在一起,不符合实情。我们修改一下基本假设:人性虽懒,但现代人要体面。在此模型中,新来的人不会选择最近的孤立位,而是选择离别人最远的孤立位。如果好几个位置都符合条件,那么懒惰本性再度发挥作用——选择这几个位置中离门最近的。
这与第一种模型非常不同。饱和所需人数不仅取决于位置总数,还与你这第一人的选择有关。令人吃惊的是,最远的位置这次不一定最好(图20.4)。
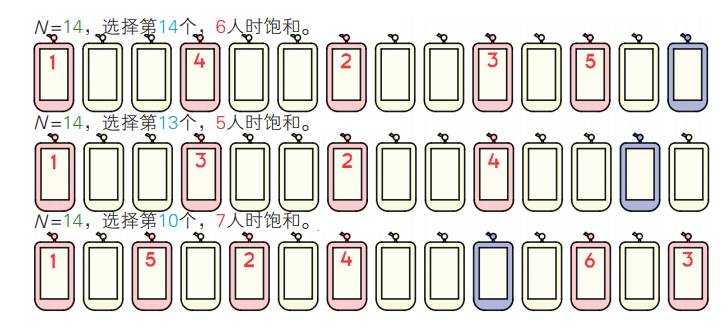
图20.4 共有14个位置,使用害羞模型
如果第一人选择最后的位置,再来5人饱和。如果他选择第10个位置,则再来6人才饱和,可记为A(14,14)=6,A(14,13)=5,A(14,10)=7。
下面来看看,如何根据位置总数N确定最好的位置。当N值较小时,很容易得出选择位置j的饱和人数,记为A(N, j)。比如N=2时,1人即饱和,于是A(2, 1)=A(2, 2)=1。当总共有3个位置时,选择两端的位置则还可容纳1人,于是A(3, 1)=A(3, 3)=2。但选择中间位置则直接饱和,于是A(3, 2)=1。
如果N值较大,就要用公式来简化计算。假设你(t=1)选择了最后位置,第二人(t=2)则会选择第一位置,第三人(t=3)要在两端已被占的情况下选择一个位置。记B(N)为两端已被占时饱和所需人数,于是有A(N, N) = 2+B(N),对称地有,A(N, 1)=2+B(N)。
如果一开始第一人选择倒数第二位置呢?此时第二人依然会选择第一位置,而且后来者谁都不会选择最后位置,这时可视为共有N-1个位置,且两端位置已被占。从第三人开始,要达到饱和所需人数为B(N-1),于是有A(N, N-1) = 2+B(N-1),同样对称地有,A(N, 2) = 2+B(N-1)。
如果你这第一人不选择两端的第一个位置、第二个位置、最后位置(N)或倒数第二位置(N-1)呢?此时,你左右都有足够多位置,后来者可以尽量靠近门,也可以尽量远离门。第3人进来后,以你的位置分成两部分,左边从位置1到位置j(你的位置),共有j个位置,右边从位置j到位置N,共N-j+1个位置。两部分互相独立,都可视为两端已被占的一组。左边可再有B(j)个人,右边可再有B(N-j+1)个人。总之,如果第一人选择j位置,则N个位置可让A(N, j) = 3+B(j)+B(N-j+1)个人安心解决内急问题。
现在,只要算出B(N)即可,也就是说,总共有N个位置且两端已被占时,达到饱和所需人数。N≤4时,两端被占即饱和,此时B(N)=0。N>4时,第一人可以选中间位置,即位置(N+1)/2(N为奇数)或N/2(N为偶数)。如上文所述,3人形成新的分区:左边从第一个位置到中间,还可再有B((N+1)/2)或B(N/2)人(N为奇数或偶数);右边从中间到最后位置,还可再有B((N+1)/2)或B(N/2+1)人(N为奇数或偶数)。
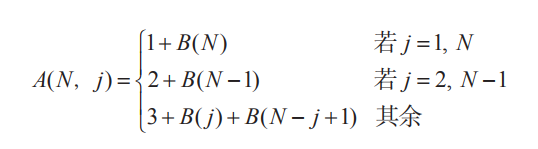
最终:
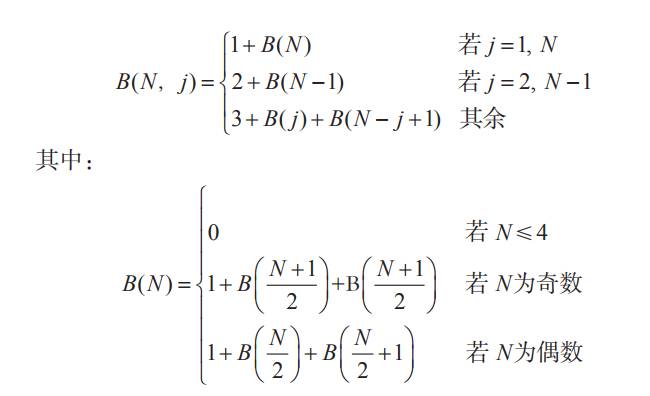
函数A和B都以递归形式定义,不到一杯啤酒的时间就能在手机上编个小程序算出来。函数B可简化为单一表达式(包含一堆对数和各种因式),但至今无法直接算出令A(N, j)最大的j值。对于给定的N值,可算出所有j值对应的A(N, j),由此可以看出,最后位置并不总是最好的选择(表20.1),并且便池利用率最高可达50%(一半便池被占用),而最低只有33%(图20.5)。
表20.1 根据便池总数不同,可算出好位置和坏位置
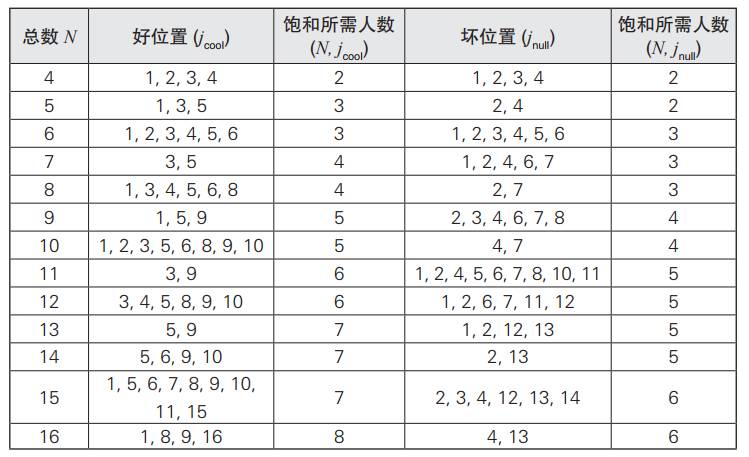
作图得出:
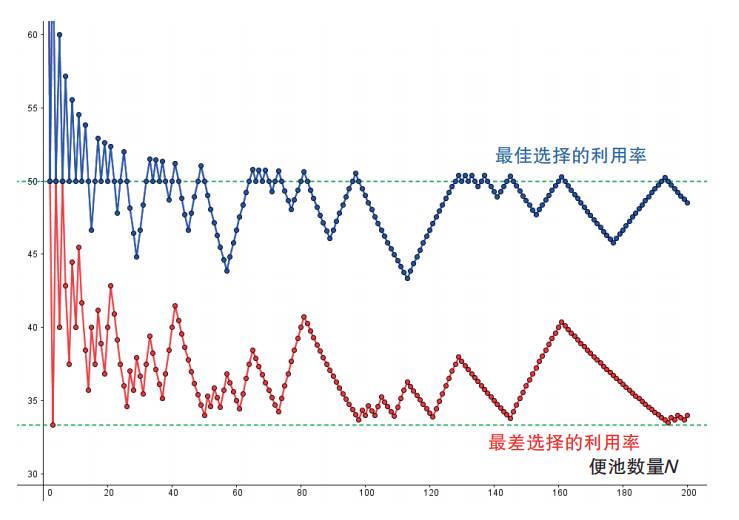
图20.5 害羞模型产生的结果比较难理解。
简单地说,便池利用率在33%到50%之间,但具体是多少,占用哪个位置会导致此利用率,都很难说。
两位大胆的数学家没有就此打住,他们还研究了“醉鬼模型”,即随机选择孤立位的模型。此模型中依然是离门越远越好。人们得到答案的同时,还能提出更多疑问,这才是好的数学题。如果部分位置已被占,选择哪个位置才好?方便的时间不会无限长,厕所里肯定是人来人往,这会不会改变最佳位置?如果不是隔开的小便器,而是沿着墙脚的小便池呢?下次泡酒吧的时候再慢慢想吧。
***
“所以说,如果我选倒数第二个位置,旁边就不会很快来人,对吧?”
“这得看你什么时候去上厕所。现在都快夜里2点了,适用醉鬼模型而不是害羞模型。我只能跟你说,现在去方便,肯定不方便!”
* 文章摘选自最新科普读物《数学也荒唐:20个脑洞大开的数学趣题》,[法]杰罗姆·科唐索著,王烈译,人民邮电出版社,2017.8。
------------------------------------
你想在情人节好好地表白心意?
你想知道公共厕所里哪个便池最安全?
你想彻底解决人类婚姻中的出轨问题?
你想苦练三个月网球就打败德约科维奇?
你想在《地产大亨》游戏里狠狠赚一笔?
这本数学书献给所有人20场数学喜剧,你从中一定能得到灵感。
终于有人认真研究如何用数学对付生活中的荒唐事了。你还在问“数学有何用处”吗?这是因为你的想象力还不够大。代数、概率、统计、几何、拓扑……书中令人捧腹的离奇问题,让貌似严肃而艰涩的数学变得既狡猾又幽默。
数学荒唐起来,有谁能拦得住?
点击上面的小程序卡片立即购买此书↑↑↑
好玩的数学以数学学习为主题,以传播数学文化为己任,以激发学习者学习数学的兴趣为目标,分享有用的数学知识、有趣的数学故事、传奇的数学人物等,为你展现一个有趣、好玩、丰富多彩的数学世界。