小波变换

编辑：Gemini

我希望能简单介绍一下小波变换，它和傅立叶变换的比较，以及它在移动平台做 motion detection 的应用。如果不做特殊说明，均以离散小波为例子。考虑到我以前看中文资料的痛苦程度，我会尽量用简单，但是直观的方式去介绍。有些必要的公式是不能少的，但我尽量少用公式，多用图。另外，我不是一个好的翻译者，所以对于某些实在翻译不清楚的术语，我就会直接用英语。我并不 claim 我会把整个小波变换讲清楚，这是不可能的事，我只能尽力去围绕要点展开，比如小波变换相对傅立叶变换的好处，这些好处的原因是什么，小波变换的几个根本性质是什么，背后的推导是什么。我希望达到的目的就是一个小波变换的初学者在看完这个系列之后，就能用 matlab 或者别的工具对信号做小波变换的基本分析并且知道这个分析大概是怎么回事。

要讲小波变换，我们必须了解傅立叶变换。要了解傅立叶变换，我们先要弄清楚什么是 ” 变换 “ 。很多处理，不管是压缩也好，滤波也好，图形处理也好，本质都是变换。变换的是什么东西呢？是基，也就是 basis 。如果你暂时有些遗忘了 basis 的定义，那么简单说，在线性代数里， basis 是指空间里一系列线性独立的向量，而这个空间里的任何其他向量，都可以由这些个向量的线性组合来表示。那 basis 在变换里面啥用呢？比如说吧，傅立叶展开的本质，就是把一个空间中的信号用该空间的某个 basis 的线性组合表示出来，要这样表示的原因，是因为傅立叶变换的本质，是。小波变换自然也不例外的和 basis 有关了。再比如你用 Photoshop 去处理图像，里面的图像拉伸，反转，等等一系列操作，都是和 basis 的改变有关。

既然这些变换都是在搞基，那我们自然就容易想到，这个 basis 的选取非常重要，因为 basis 的特点决定了具体的计算过程。一个空间中可能有很多种形式的 basis ，什么样的 basis 比较好，很大程度上取决于这个 basis 服务于什么应用。比如如果我们希望选取有利于压缩的话，那么就希望这个 basis 能用其中很少的向量来最大程度地表示信号，这样即使把别的向量给砍了，信号也不会损失很多。而如果是图形处理中常见的线性变换，最省计算量的完美 basis 就是 eigenvector basis 了，因为此时变换矩阵 T 对它们的作用等同于对角矩阵 ( Tv_n = av_n ， a 是 eigenvalue ) 。总的来说，抛开具体的应用不谈，所有的 basis ，我们都希望它们有一个共同的特点，那就是，容易计算，用最简单的方式呈现最多的信号特性。

好，现在我们对变换有了基本的认识，知道他们其实就是在搞基。当然，搞基也是分形式的，不同的变换，搞基的妙处各有不同。接下来先看看，傅立叶变换是在干嘛。

傅立叶级数最早是 Joseph Fourier 这个人提出的，他发现，这个 basis 不仅仅存在与 vector space ，还存在于 function space 。这个 function space 本质上还是一个 linear vector space ，可以是有限的，可以是无限的，只不过在这个空间里， vector 就是 function 了，而对应的标量就是实数或者复数。在 vector space 里，你有 vector v 可以写成 vector basis 的线性组合，那在 function space 里， function f(x) 也可以写成对应 function basis 的线性组合，也有 norm 。你的 vector basis 可以是正交的，我的 function basis 也可以是正交的（比如 sin(t) 和 sin(2t) ）。唯一不同的是，我的 function basis 是无穷尽的，因为我的 function space 的维度是无穷的。好，具体来说，那就是现在我们有一个函数， f(x) 。我们希望将它写成一些 cos 函数和一些 sin 函数的形式，像这样

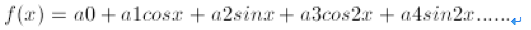
again ，这是一个无限循环的函数。其中的 1 ， cosx, sinx, cos2x ….. 这些，就是傅立叶级数。傅立叶级数应用如此广泛的主要原因之一，就是它们这帮子 function basis 是正交的，这就是有趣的地方了。为什么 function basis 正交如此重要呢？我们说两个 vector 正交，那就是他俩的内积为 0 。那对于 function basis 呢？ function basis 怎么求内积呢？

现在先复习一下 vector 正交的定义。我们说两个 vector v,w 如果正交的话，应符合：

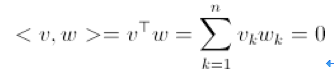
那什么是 function 正交呢？假设我们有两个函数 f(x) 和 g(x) ，那是什么？我们遵循 vector 的思路去想，两个 vector 求内积，就是把他们相同位置上对应的点的乘积做一个累加。那移过来，就是对每一个 x 点，对应的 f 和 g 做乘积，再累加。不过问题是， f 和 g 都是无限函数阿， x 又是一个连续的值。怎么办呢？向量是离散的，所以累加，函数是连续的，那就是 ……. 积分！

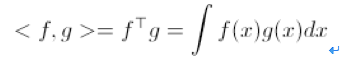
我们知道函数内积是这样算的了，自然也就容易证明，按照这个形式去写的傅立叶展开，这些级数确实都是两两正交的。证明过程这里就不展开了。好，下一个问题就是，为什么它们是正交 basis 如此重要呢？这就牵涉到系数的求解了。我们研究了函数 f ，研究了级数，一堆三角函数和常数 1 ，那系数呢？ a0, a1, a2 这些系数该怎么确定呢？好，比如我这里准备求 a1 了。我现在知道什么？信号 f(x) 是已知的，傅立叶级数是已知的，我们怎么求 a1 呢？很简单，把方程两端的所有部分都求和 cosx 的内积，即：

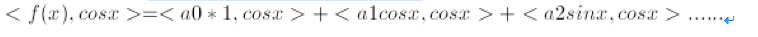
然后我们发现，因为正交的性质，右边所有非 a1 项全部消失了，因为他们和 cosx 的内积都是 0 ！所有就简化为

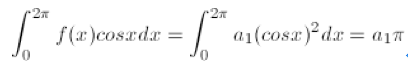
这样， a1 就求解出来了。到这里，你就看出正交的奇妙性了吧 :)

好，现在我们知道，傅立叶变换就是用一系列三角波来表示信号方程的展开，这个信号可以是连续的，可以是离散的。傅立叶所用的 function basis 是专门挑选的，是正交的，是利于计算 coefficients 的。但千万别误解为展开变换所用的 basis 都是正交的，这完全取决于具体的使用需求，比如泰勒展开的 basis 就只是简单的非正交多项式。

有了傅立叶变换的基础，接下来，我们就看看什么是小波变换。首先来说说什么是小波。所谓波，就是在时间域或者空间域的震荡方程，比如正弦波，就是一种波。什么是波分析？针对波的分析拉（囧）。并不是说小波分析才属于波分析，傅立叶分析也是波分析，因为正弦波也是一种波嘛。那什么是小波呢？这个 ” 小 “ ，是针对傅立叶波而言的。傅立叶所用的波是什么？正弦波，这玩意以有着无穷的能量，同样的幅度在整个无穷大区间里面振荡，像下面这样：

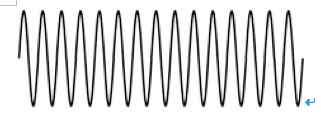
那小波是什么呢？是一种能量在时域非常集中的波。它的能量是有限的，而且集中在某一点附近。比如下面这样：

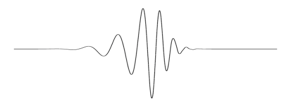
这种小波有什么好处呢？它对于分析瞬时时变信号非常有用。它有效的从信号中提取信息，通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析，解决了傅立叶变换不能解决的许多困难问题。恩，以上就是通常情况下你能在国内网站上搜到的小波变换文章告诉你的。但为什么呢？这是我希望在这个系列文章中讲清楚的。不过在这篇文章里，我先点到为止，把小波变换的重要特性以及优点 cover 了，在下一篇文章中再具体推导这些特性。

小波变换的本质和傅立叶变换类似，也是用精心挑选的 basis 来表示信号方程。每个小波变换都会有一个 mother wavelet ，我们称之为母小波，同时还有一个 scaling function ，中文是尺度函数，也被成为父小波。任何小波变换的 basis 函数，其实就是对这个母小波和父小波缩放和平移后的集合。下面这附图就是某种小波的示意图：

从这里看出，这里的缩放倍数都是 2 的级数，平移的大小和当前其缩放的程度有关。这样的好处是，小波的 basis 函数既有高频又有低频，同时还覆盖了时域。对于这点，我们会在之后详细阐述。

小波展开的形式通常都是这样（注意，这个只是近似表达，严谨的展开形式请参考 第二篇 http://www.kunli.info/2011/01/27/fourier-wavele…otion-signal-2/ ）：

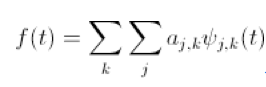
其中的 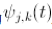就是小波级数，这些级数的组合就形成了小波变换中的基 basis 。和傅立叶级数有一点不同的是，小波级数通常是 orthonormal basis ，也就是说，它们不仅两两正交，还归一化了。小波级数通常有很多种，但是都符合下面这些特性：

1. 小波变换对不管是一维还是高维的大部分信号都能 cover 很好。这个和傅立叶级数有很大区别。后者最擅长的是把一维的，类三角波连续变量函数信号映射到一维系数序列上，但对于突变信号或任何高维的非三角波信号则几乎无能为力。

2. 围绕小波级数的展开能够在时域和频域上同时定位信号，也就是说，信号的大部分能量都能由非常少的展开系数，比如 a_{j,k} ，决定。这个特性是得益于小波变换是二维变换。我们从两者展开的表达式就可以看出来，傅立叶级数是 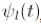，而小波级数是 。

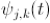3. 从信号算出展开系数 a 需要很方便。普遍情况下，小波变换的复杂度是 O(Nlog(N)) ，和 FFT 相当。有不少很快的变换甚至可以达到 O(N) ，也就是说，计算复杂度和信号长度是线性的关系。小波变换的等式定义，可以没有积分，没有微分，仅仅是乘法和加法即可以做到，和现代计算机的计算指令完全 match 。

可能看到这里，你会有点晕了。这些特性是怎么来的？为什么需要有这些特性？具体到实践中，它们到底是怎么给小波变换带来比别人更强的好处的？计算简单这个可能好理解，因为前面我们已经讲过正交特性了。那么二维变换呢？频域和时域定位是如何进行的呢？恩，我完全理解你的感受，因为当初我看别的文章，也是有这些问题，就是看不到答案。要说想完全理解小波变换的这些本质，需要详细的讲解，所以我就把它放到下一篇了。

接下来，上几张图，我们以一些基本的信号处理来呈现小波变换比傅立叶变换好的地方，我保证，你看了这个比较之后，大概能隐约感受到小波变换的强大，并对背后的原理充满期待 :)

假设我们现在有这么一个信号：

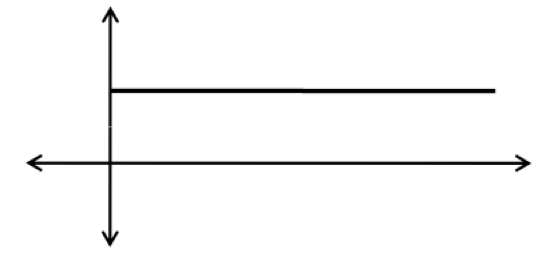
看到了吧，这个信号就是一个直流信号。我们用傅立叶将其展开，会发现形式非常简单：只有一个级数系数不是 0 ，其他所有级数系数都是 0 。好，我们再看接下来这个信号：

简单说，就是在前一个直流信号上，增加了一个突变。其实这个突变，在时域中看来很简单，前面还是很平滑的直流，后面也是很平滑的直流，就是中间有一个阶跃嘛。但是，如果我们再次让其傅立叶展开呢？所有的傅立叶级数都为非 0 了！为什么？因为傅立叶必须用三角波来展开信号，对于这种变换突然而剧烈的信号来讲，即使只有一小段变换，傅立叶也不得不用大量的三角波去拟合，就像这样：

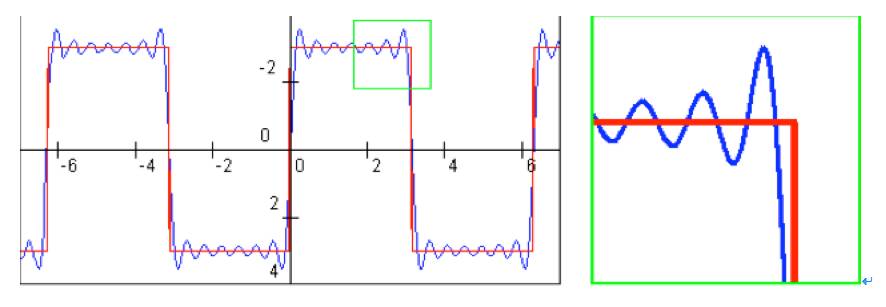
看看上面这个图。学过基本的信号知识的朋友估计都能想到，这不就是 Gibbs 现象么？ Exactly 。用比较八股的说法来解释， Gibbs 现象是由于展开式在间断点邻域不能均匀收敛所引起的，即使在 N 趋于无穷大时，这一现象也依然存在。其实通俗一点解释，就是当变化太 sharp 的时候，三角波 fit 不过来了，就凑合出 Gibbs 了 :)

接下来我们来看看，如果用刚才举例中的那种小波，展开之后是这样的：

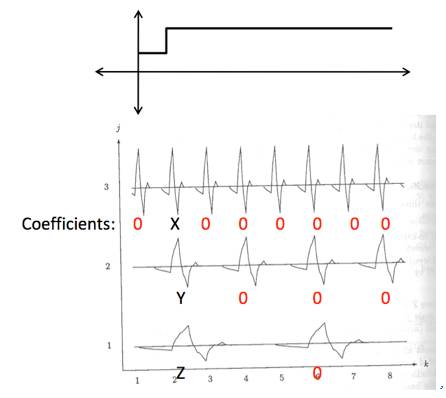
看见了么？只要小波 basis 不和这个信号变化重叠，它所对应的级数系数都为 0 ！也就是说，假如我们就用这个三级小波对此信号展开，那么只有 3 个级数系数不为 0 。你可以使用更复杂的小波，不管什么小波，大部分级数系数都会是 0 。原因？由于小波 basis 的特殊性，任何小波和常量函数的内积都趋近于 0 。换句话说，选小波的时候，就需要保证母小波在一个周期的积分趋近于 0 。正是这个有趣的性质，让小波变换的计算以及对信号的诠释比傅立叶变换更胜一筹！原因在于，小波变换允许更加精确的局部描述以及信号特征的分离。一个傅立叶系数通常表示某个贯穿整个时间域的信号分量，因此，即使是临时的信号，其特征也被强扯到了整个时间周期去描述。而小波展开的系数则代表了对应分量它当下的自己，因此非常容易诠释。

小波变换的优势不仅仅在这里。事实上，对于傅立叶变换以及大部分的信号变换系统，他们的函数基都是固定的，那么变换后的结果只能按部就班被分析推导出来，没有任何灵活性，比如你如果决定使用傅立叶变换了，那 basis function 就是正弦波，你不管怎么 scale ，它都是正弦波，即使你举出余弦波，它还是移相后的正弦波。总之你就只能用正弦波，没有任何商量的余地。而对于小波变换来讲，基是变的，是可以根据信号来推导或者构建出来的，只要符合小波变换的性质和特点即可。也就是说，如果你有着比较特殊的信号需要处理，你甚至可以构建一个专门针对这种特殊信号的小波 basis function 集合对其进行分析。这种灵活性是任何别的变换都无法比拟的。总结来说，傅立叶变换适合周期性的，统计特性不随时间变化的信号 ; 而小波变换则适用于大部分信号，尤其是瞬时信号。它针对绝大部分信号的压缩，去噪，检测效果都特别好。

在上一篇中讲到，每个小波变换都会有一个 mother wavelet ，我们称之为母小波，同时还有一个 father wavelet ，就是 scaling function 。而该小波的 basis 函数其实就是对这个母小波和父小波缩放和平移形成的。缩放倍数都是 2 的级数，平移的大小和当前其缩放的程度有关。

还讲到，小波系统有很多种，不同的母小波，衍生的小波基就完全不同。小波展开的近似形式是这样：

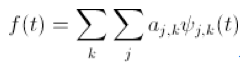
其中的 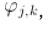就是小波级数，这些级数的组合就形成了小波变换中的基 basis 。和傅立叶级数有一点不同的是，小波级数通常是 orthonormal basis ，也就是说，它们不仅两两正交，还归一化了。

我们还讲了一般小波变换的三个特点，就是小波级数是二维的，能定位时域和频域，计算很快。但我们并没有深入讲解，比如，如何理解这个二维？它是如何同时定位频域和时域的？

在这一篇文章里，我们就来讨论一下这些特性背后的原理。

首先，我们一直都在讲小波展开的近似形式。那什么是完整形式呢？之前讲到，小波 basis 的形成，是基于基本的小波函数，也就是母小波来做缩放和平移的。但是，母小波并非唯一的原始基。在构建小波基函数集合的时候，通常还要用到一个函数叫尺度函数， scaling function ，人们通常都称其为父小波。它和母小波一样，也是归一化了，而且它还需要满足一个性质，就是它和对自己本身周期平移的函数两两正交：

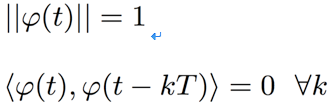
另外，为了方便处理，父小波和母小波也需要是正交的。可以说，完整的小波展开就是由母小波和父小波共同定义的。

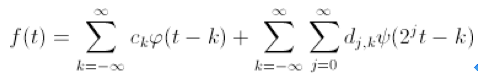
其中 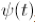是母小波， 是父小波。需要提醒一点的是，这个正交纯粹是为了小波分析的方便而引入的特性，并不是说小波变换的基就一定必须是正交的。但大部分小波变换的基确实是正交的，所以本文就直接默认正交为小波变换的主要性质之一了。引入这个父小波呢，主要是为了方便做多解析度分析（ multiresolution analysis, MRA ）。说到这里，你的问题可能会井喷了：好好的为什么出来一个父小波呢？这个 scaling function 是拿来干嘛的？它背后的物理意义是什么？ wavelet function 背后的物理意义又是什么？这个多解析度分析又是什么呢？不急，下面，我们围绕一个例子来巩固一下前面的知识，同时再引出新的特性。

假设我们有这样一个信号：

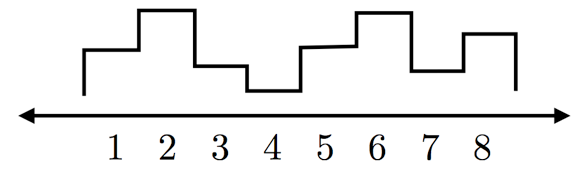
该信号长度为 8 ，是离散的一维信号。我们要考虑的，就是如何用小波将其展开。为了方便讲解，我们考虑最简单的一种小波，哈尔小波。下面是它的一种母小波：

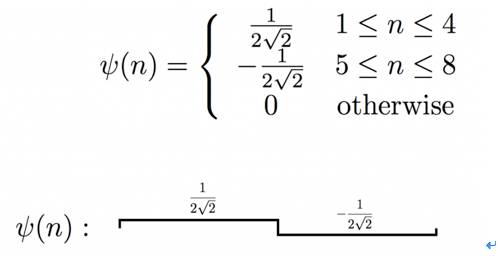
那如何构建基于这个母小波的基呢？刚才提到了，要缩放，要平移。我们先试试缩放，那就是 ψ(2n) ：

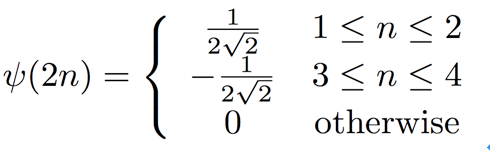
但这样的话，它与自己的内积就不是 1 了，不符合小波基 orthonormal 的要求，所以我们要在前面加一个系数根号二，这样我们就得到了另一个哈尔小波的 basis function ：

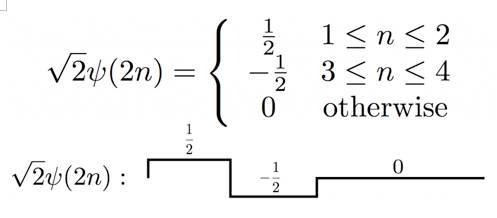
同理，我们可以一直这样推广下去做 scale ，得到 4n ， 8n ， ……. 下的 basis function 。当然在这个例子里，我们信号长度就是 8 ，所以做到 4n 就够了。但推广来说，就是这种 scaling 对母小波的作用为 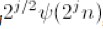，这是归一化后的表示形式。

平移的话也很简单，我们可以对母小波进行平移，也可以对 scale 之后的 basis function 进行平移。比如对上一幅图中的 basis function 进行平移，就成了

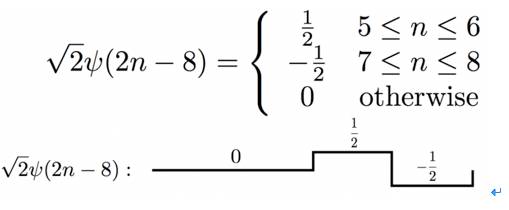
看得出来，平移后的 basis function 和母小波以及仅仅 scale 过的小波，都是正交的，附合小波 basis 的特点。如果我们用 ψ(n) 来表示这个 mother wavelet ，那么这些 orthonormal basis 函数可以写成：

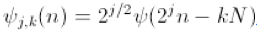
这里的 k 是可以看成时域的参数，因为它控制着小波基时域的转移，而 j 是频域的参数，因为它决定了小波基的频率特性。看到这里，你应该会感觉很熟悉，因为这里的平移和变换本质和刚才对 scaling function 的平移变换是一模一样的。

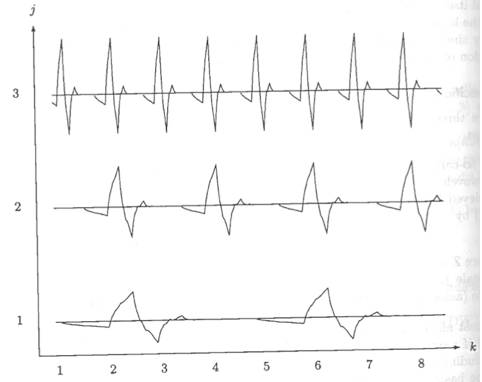
这样，我们就有了针对此信号 space 的哈尔小波 basis 组合：

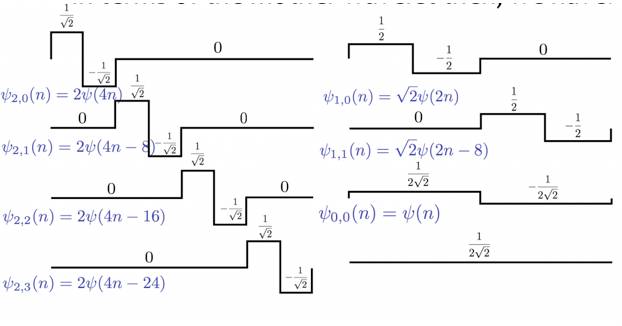
图 1

可以看出，我们用到了三层频率尺度的小波函数，每往下一层，小波的数量都是上面一层的两倍。在图中，每一个小波基函数的表达形式都写在了波形的下面。

等等，你可能已经发现了，有问题。这里为什么多了个没有函数表达式的波形呢？这货明显不是 wavelet function 阿。没错，它是之前提到的 scaling function ，也就是父小波。然后你可能就会问，为啥这个凭空插了一个 scaling function 出来呢？明明目标信号已经可以用纯的小波基组合表示了。是，确实是，就算不包括 scaling function ，这些小波函数本身也组成了正交归一基，但如果仅限于此的话，小波变换也就没那么神奇的功效了。引入这个 scaling function ，才能引入我们提到的多解析度分析的理论，而小波变换的强大，就体现在这个多解析度上。那在这里，我们怎么用这个多解析度呢？这个哈尔小波 basis 组合是怎么通过多解析度推导出来的呢？

话说在数学定义中，有一种空间叫 Lebesgue 空间，对于信号处理非常重要，可以用 L^p(R) 表示，指的是由 p 次可积函数所组成的函数空间。我们在小波变换中要研究的信号都是属于 L^2(R) 空间的，这个空间是 R 上的所有处处平方可积的可测函数的集合，这样就等于对信号提出了一个限制，就是信号能量必须是有限的，否则它就不可积了。小波变换的定义都是基于但不限于 L^2(R) 中的信号的。这玩意的特性要具体解释起来太数学了，牵涉到太多泛函知识，我就不在这里详述了。而且老实说我也没能力完全讲清楚，毕竟不是学这个的，有兴趣可以参考 wiki 。总之你记住，小波变换研究中所使用的信号基本都是平方可积的信号，但其应用不限于这种信号，就行了。

对 L^2(R) 空间做 MRA 是在干嘛呢？就是说，在 L^2(R) 空间中，我们可以找出一个嵌套的空间序列，并有下列性质：

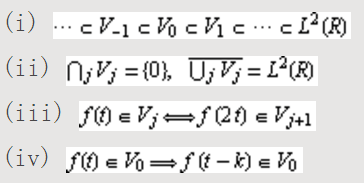
(v) 有这样一个方程 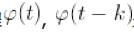是的 orthonormal basis 。

我来简单解释一下这些性质。这个 V_j 都是 L^2(R) 空间中的子空间，然后他们是由小到大的，交集是 {0} ，因为这是最小的子空间，并集就是 L 空间。是不是有点难以理解？没关系，看看下面这个图就清楚了：

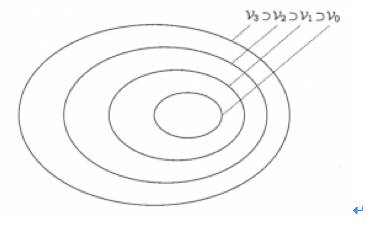
这个图是圈圈套圈圈，最里面的圈是 V0 ，之后分别是 V1 ， V2 ， V3 ， V4 。那他们有趣的性质就是，假如有一个函数 f(t) 他属于一个某空间，那你将其在时域上平移，它还是属于这个空间。但如果你对它频域的放大或缩小，它就会相应移到下一个或者上一个空间了。

同时我们还知道，你要形容每一个空间的话，都需要有对应的 orthonormal basis ，这是必然的，那对于 V0 来讲，它的 orthonormal basis 就是

这一系列函数是什么呢？是 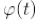的时域变换，而且我们刚才也说了，时域上平移，是不会跳出这个空间的。这样，我们就可以说，由这一系列 basis 所定义的 L^2(R) 子空间 V0 被这些 basis 所 span ，表示成：

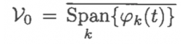
k 从负无穷到正无穷。上面的 bar 表示这是一个闭包空间，也就是说

这样，我们就定义了基本的 V0 这个子空间。刚才说了，这个子空间的基都是对 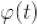的整数时域变换，这里我们称 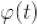为 scaling function ，所以换个说法，就是说这里整个子空间 V0 ，由 scaling function 和其时域变换的兄弟们 span 。

当然，如果这个 scaling function 只是用来代表一个子空间的，那它的地位也就不会这么重要了。刚才我们提到，这个嵌套空间序列有一个性质，。这就是这个函数，如果你对它频域的放大或缩小，它就会相应移到下一个或者上一个空间了。这个性质就有意思了，它代表什么呢？对于任何一个包含 V0 的更上一层的空间来讲，他们的基都可以通过对 scaling function 做频域的 scale 后再做时域上的整数变换得到！推广开来就是说，当

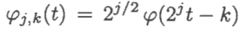
我们有

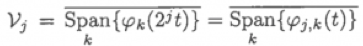
这也就意味着，对于任何属于 V_j 空间的函数 f(t) ，都可以表示为：

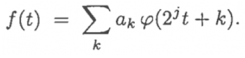
到这里，我们就明白这些个子空间和那个凭空冒出来的 scaling function 的作用了。 scaling 的构建这些不同的子空间的基础，当 j 越大的时候，每一次你对频率变换后的 scaling function 所做的时域上的整数平移幅度会越小，这样在这个 j 子空间里面得到的 f(t) 表示粒度会很细，细节展现很多。反之亦然。通俗点说，就是对 scaling function 的变换平移给你不同的子空间，而不同的子空间给你不同的分辨率，这样你就可以用不同的分辨率去看目标信号。

下面就是时候看看什么是 MRA equation 了，这是更加有趣，也是更加核心的地方。通过刚才的讲解， V0 属于 V1 ，那 scaling function 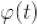是在 V0 中的，自然也在 V1 中了。我们把他写成 V1 的基的线性组合，那就是

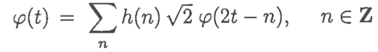
其中的 h(n) 是 scaling function 的系数，也叫做 scaling filter 或者 scaling vector ，可以是实数，也可以是虚数。根号 2 是为了维持 norm 为 1 的。看，在这个公式里，我们就把属于 V0 的函数用 V1 的基表示出来了。同理，我们可以循环如此，把属于 V0 的 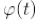在 V2, V3, …, Vn 中表示出来。这些方程就是 MRA equation ，也叫 refinement equation ，它是 scaling function 理论的基础，也是小波分析的基础之一。

好，稍微总结一下。到现在，已经讲了关于 scaling function 的基本理论知识，知道了信号空间可以分为不同精细度的子空间，这些子空间的 basis 集合就是 scaling function 或者频率变换之后的 scaling function ，如下图所示：

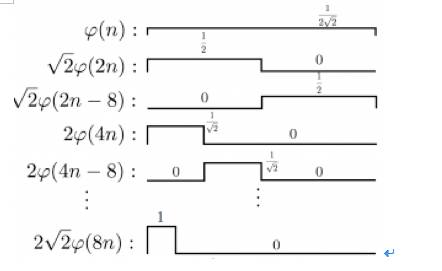
上图就是四个子空间的 basis 集合的展览。通过前面的讨论，我们还知道，一开始的 scaling function 可以通过更精细的子空间的 scaling function （它们都是对应子空间的 basis ）来构建。比如

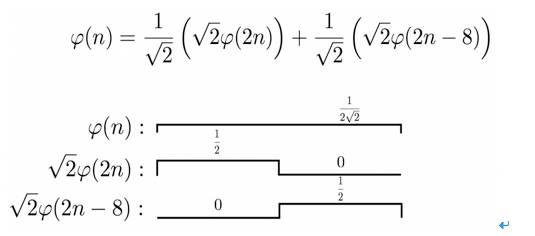
对于更加 finer 的 scale ：

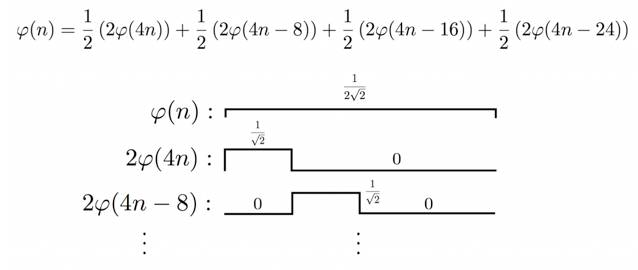
图 2
依此类推。实际上，对于任何 scale 和 translate 过的 scaling function ，都可以用更加精细的 scale 层面上的 scaling function 构建出来。

然后，我们有各种 scale 下的 scaling function 了，该看看它们分别所对应的嵌套的空间序列了。先看看 V0 ，自然就是以基本的 scaling function 为基础去 span 出来的：

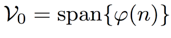
这个不新鲜，刚才就讲过了。这个子空间代表什么样的信号？常量信号。道理很简单，这个 scaling function 在整个信号长度上，没有任何变化。继续往下看：

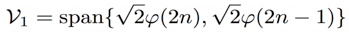
这个相比 V0 更加 finer 的子空间，代表着这样一种信号，它从 1-4 是常量，从 5-8 是另一个常量。同理我们有：

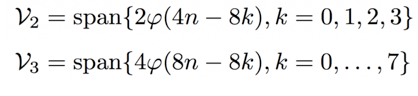
V2 代表的信号，是分别在 1 ， 2; 3 ， 4; 5 ， 6; 7 ， 8 上有相同值的信号。那么 V3 呢？则表示任何信号，因为对于 V3 来讲，任何一个时间刻度上的值都可以不一样。而且现在，我们也可以通过上面的一些 scaling functions 的波形验证了之前提到的多解析度分析中的一个核心性质，那就是：

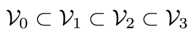
我们之前讲了一堆多解析度的理论，但直到现在，通过这些图形化的分析，我们可能才会真正理解它。那好，既然我们有一个现成的信号，那就来看看，对这个信号作多解析度分析是啥样子的：

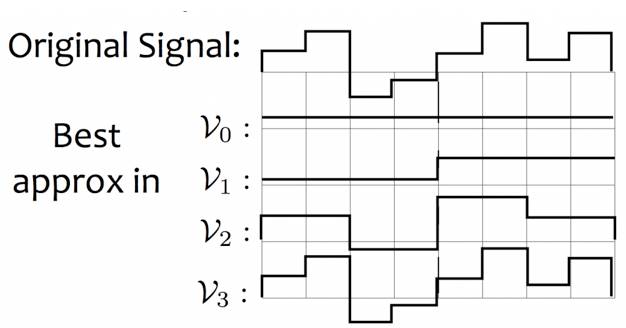
你看，在不同的子空间，对于同一个信号就有不同的诠释。诠释最好的当然是