数学中的悖论或者谬误，常常都是因为违反某条数学规则或数学定律而导致的结果。这使得这些悖论成为说明这些规则的优秀载体，因为它们的违规导致了某些相当“奇异”的结果，比如说1=2，或1=0，简直荒谬！它们显然具有娱乐性，因为它们非常微妙地将我们引向了一个不可能的结论。通向这个怪异结果的每一步看起来似乎都是正确的，这个事实常常令我们倍感困惑。这相当具有激励作用，并且会使结论令人印象深刻得多。
同样，这也是探究数学边界的一个良好资源。为什么不允许除以0？为什么根式的乘积并不总是等于乘积的根式？这只是众多悖论中的几个问题，揭示这些“滑稽”的结果很有乐趣，而且它们具有很高的研究价值。
一、一切都相等吗？
拥有迷人内容的标题显然是荒谬可笑的！不过从下面的范例中你会看到，情况也许并非如此。我们从一个很容易被接受的等式开始：
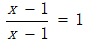接下去的每一行都可以很容易地用初等代数来说明。代数方面没有任何错误。
当x=1时，1,2,3,4,…，n这些数中的每一个都等于
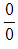，这就导致它们全都彼此相等。当然，这不可能是正确的。出于这个原因，我们定义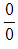是无意义的。在数学中，为了避免一些荒谬的陈述，我们会做出一些定义，从而使事情有意义或不产生矛盾，正如这里的情况所表明的。
二、-1不等于+1
大家应该知道
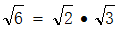，于是可能会推断
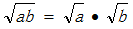。由此，我们计算
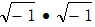时，可能会这样：
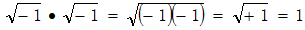；也可能这样计算：
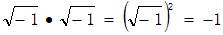。如果这两种算法都是正确的，那么这就意味着1=-1，因为两者都等于
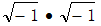。显然，这不可能是正确的。
哪里可能出错了呢？再一次，当我们违反一条数学规则时，就出现了一个“谬误”这里我们定义a和b中至少有一个是非负数时，
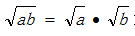才成立。这就意味着按照
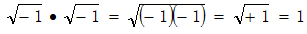进行计算的人错了。
三、不能除以0
大家都知道除以0是被禁止的。事实上，在数学戒律的清单上，这一点高居榜首。不过，为什么不允许除以0呢？数学王国里的万事万物都整齐地各就各位，我们对数学中的秩序和美丽引以为傲。当某件可能破坏这种秩序的事情出现时，我们就直接作出规定以适应我们的需要。这恰恰就是面对除以0的情况时发生的事情。通过解释为什么要提出这些“规则”，大家会对于数学的本质产生一种更加深入的洞察。因此，让我们来为这条戒律赋予某种意义。
考虑
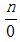的商，其中
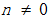。在不承认那条除以0的戒律的情况下，让我们推测（猜想）这个商可能等于什么。让我们假设它为p，可以通过乘法
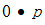看它是否等于n来检验，因为这就是除法运算正确时应该得到的结果。因为
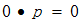，我们知道
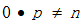。因此，不管商p取什么值都不能使这道除法成立，所以我们规定禁止除以0。
还有一个更令人信服的例子让我们要去禁止除以0，那就是向大家展示这会导致与一个已被接受的事实产生矛盾，这个事实就是
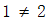。如果除以0被接受，那么就会得到
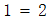，这显然是一个谬误。这是对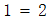的证明：
在除以
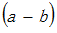那一步中，我们实际上是在除以0，这是因为
，所以
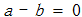。这最终使我们得出了一个荒谬的结果，从而令我们别无选择，只能禁止除以0。
四、一个无穷级数的谬论
如果不考虑收敛级数的概念，我们就会陷入以下困境。
令
不过，如果我们用另一种方法对其进行分组，就会得到下式：
令
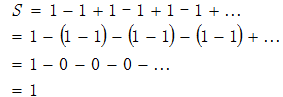
因此，既然
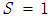且
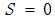，那么就有
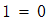。这一论证过程出了什么错？
如果这还不够让你心烦，那么请考虑下面这个论证过程：
令
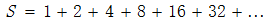（1）
这里的S显然是正的。
又
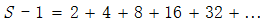（2）
现在，将（1）式两边乘以2，我们就得到：
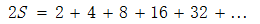（3）
把（2）式带入（3）式，就有
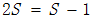，从而
。
这会使我们得到-1是正数的奇怪结论，事实上，这里的漏洞与收敛有关。
五、令人迷惑的悖论
讨论悖论是很有乐趣的，而且这些悖论中常常会包含某条非常重要的信息，通过这项娱乐我们会学到很多东西。例如：2磅=32盎司，0.5磅=8盎司，相乘得到1磅=256盎司！
这个悖论的关键在于：这里的两个单位没有得到恰当的处理，用下面这个例子可以给出最佳的回答：2英尺=24英寸，0.5英尺=6英寸，相乘得到1平方英尺=144平方英寸，即1英尺=12英寸。
