在该篇文章中讲了隐马尔科夫模型（HMM）一基本模型与三个基本问题
隐马尔科夫模型-基本模型与三个基本问题
，这篇文章总结一下隐马尔科夫链（HMM）中的前向与后向算法，首先给出这俩个算法是为了解决HMM的第一个基本问题。
先回忆一下第一个问题：
第一个问题是求，给定模型的情况下，求某种观测序列出现的概率。
比如，给定的HMM模型参数已知，求出三天观察是(Dizzy,Cold,Normal)的概率是多少？
(
对应的HMM模型参数已知的意思，就是说的A(trainsition_probability),B(emission_probability),pi矩阵是已经知道的。)
相关条件如下图所示：
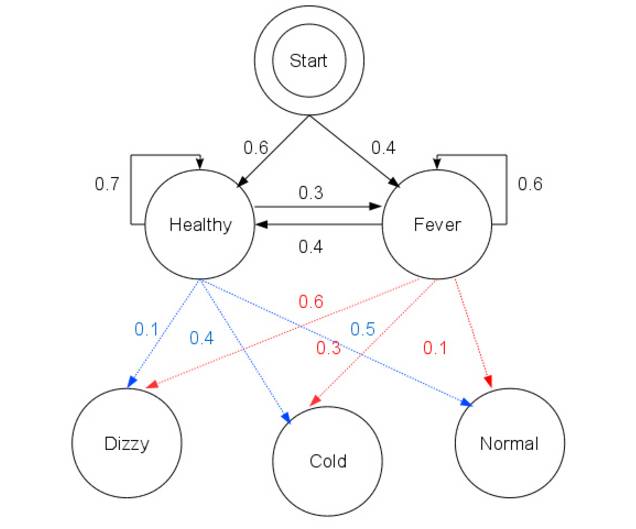由上图所示，也就是说，可以写成如下代码：
trainsition_probability = [[0.7,0.3],[0.4,0.6]]
emission_probability = [[0.5,0.4,0.1],[0.1,0.3,0.6]]
pi = [0.6,0.4]
在第一个问题中，我们需要求解出三天观察是(Dizzy,Cold,Normal)的概率是多少？
这里为了演示简单，我只求解出俩天观察为(Dizzy,Cold)的概率是多少！
这个问题太好求解了，最暴力的方法就是将路径全部遍历一遍。下面尽可能通
俗易懂的说明一下：
首先画出时间序列状态图如下：
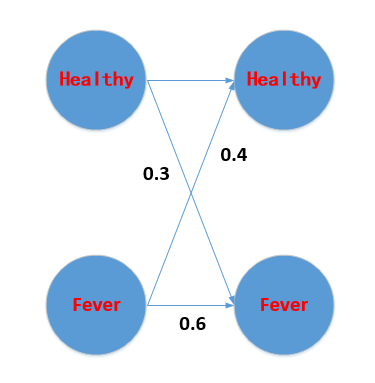
下面，我详细走一遍一条路径的暴力算法，这样既可以避开公式的晦涩，也不失正确性。其它路径完全类似
第一天为Healthy的概率为：0.6
在第一天为Healthy的基础上，观察为Dizzy的概率为：P（Dizzy|Healthy）=0.6*
P(Healthy->Dizzy)=0.6*
0.1=0.06
然后求出在第一天为Healthy的基础上，并且第一天表现为Dizzy的前提下，第二天也为Healthy的概率为：
P(Healthy|Healthy,Dizzy)
= P(Dizzy|healthy)*
07 = 0.06*
0.7
上面求完的时候，代表下图中的红线已经转移完了。
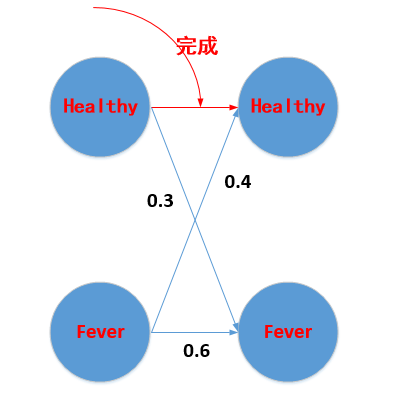
好，那么当在前面基础上，第二天观察为Cold的概率为：
P(Cold|(Healthy,Dizzy),(Healthy)) = P(Healthy|Healthy,Dizzy)*
0.4 = 0.06*
0.7*
0.4
现在我们已经完成一条路径的完整结果了。
就是在第一天隐含状态为Healthy和第二天隐含状态为Healthy的基础上，观察序列为Dizzy，Cold的概率为
P（Dizzy,Cold|Healthy,Healthy） = 0.06*
0.7*
0.4=0.0168
那么同理，我们就可以求出其它三条路径。
（1）在第一天隐含状态为Healthy和第二天隐含状态为Fever的基础上，观察序列为Dizzy，Cold的概率
（2）在第一天隐含状态为Fever和第二天隐含状态为Healthy的基础上，观察序列为Dizzy，Cold的概率
（3）在第一天隐含状态为Fever和第二天隐含状态为Fever的基础上，观察序列为Dizzy，Cold的概率
然后最后的第一个问题的结果就是将这四个结果
相加
起来就可以了。是不是很简单，那么为了还需要
前向后向算法
来解决这个事呢？
其实这个算法在现实中是不可行的。我给的例子由于是为了讲解容易，状态值和观察值都很小，但是实际中的问题，
隐状态的个数是非常大的。
那么我们的计算量是不可以忍受的。
我们可以稍微估计一下，加入状态值是N个，观察值是K个。总共观察长度为T。
那么我们的路径总个数就是N的T次方,我的天，
这个复杂度已经接受不了了，到达了每个隐含状态的时候，还需要算一遍观察值出现的概率（每个隐状态计算一遍到观察值的概率）。又要乘以NT（当然这已经对前面很大复杂度构成不了多少作用了）
所以我们得出结论，
暴力法在这里并不实用，于是就引出了前向后向算法。它们都是基于动态规划思想求解
。下面介绍一下：
