
作者:大罕老师(原创)
从形式看x=x+1是方程。含有未知数的等式叫方程,它是含有未知数的等式,所以是方程。从实质看x=x+1不是方程。它化简后得0=1,是矛盾的等式且不含未知数了,所以它不是方程了吗?
这样一些似是而非的问题,在我们中学数学教育界普遍存在着不同的看法,也有一些争论。所以,我们讨论一下是非常必要的。考虑到学生不适宜接受也没必要接受以下的讨论内容,因此,
有关这一类概念的问题,建议不要出现在练习题中,更不要出现在考卷上
。同时需要声明的是,以下意见,并不是笔者的首创,也不是“独辟蹊径”,只是在认识上的一种趋同。
数学的严谨,在不同教学环境下(中学和大学),处理起来是有所不同的。有时,严谨是第二位的,可接受性才是第一位的。在中学范围内就是这样的。
含有未知数的等式,这样定义方程是从形式上加以定义。也就是“一眼看去”,是含有未知数的等式,都叫方程。x=x+1,是等式,出现有未知数x,所以它是方程,是解集为空集的方程。
所谓“一眼看去”,就是“不动手脚”的原状,不要整理它
(去括号、约分、合并同类项等),是什么就是什么。这不仅是省力,更是省心,无须考虑等价性,从而避免一些无谓的争论。
例如,我们认为y=log2x是对数函数,而认为y=2log4x不是对数函数。有人站出来说话了:所谓函数,本质上是两个数集之间的映射关系。y=log2x与y=2log4x本质上是同一种映射关系,为什么一个是对数函数,另一个不是?
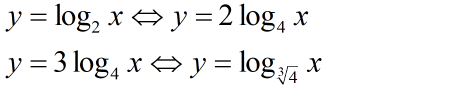
好了,就牵就你,就说“y=2log4x是对数函数”,那么试问:y=3log4x是不是对数函数呢?按你的方式,
因为y=3log(4)x<=>y=log(4^(1/3))x,
而y=log(4^(1/3))x是对数函数,
所以y=3log(4)x是对数函数。
于是,一般地,形如y=blog(a)x (b≠0,a>0,且a≠1)的函数是对数函数。
其它的函数是不是也可以仿照这个办法审视一遍呢?当然可以呀!
这时我们发现,坏事了,坏事了!对数函数的定义不是乱套了吗?其它函数的定义不是也可能乱套了吗?
而且,这样的“公说公有理,婆就婆有理”的乱象,对我们学习函数有帮助吗?
完全无益,毫无帮助!那么,我们还是回归到形式吧,以形式定义方程,以形式来定义什么叫分式,什么叫二次根式,什么叫基本初等函数。
定义中学数学中的概念时应以形式为准,不是因为我们不看重“实质”,而是因为看重实质后会带来一些不必要的争议。
如果采用折中的方案,有些概念看形式,有些则看实质,这样好不好呢?不好,同样会带来争议。于是,如其在这一人为规定的不那么紧要的定义上争论不休,不如我们找到一个共识,即以形式为准,这样的话,或许就能消除在概念上的人为的干扰。
最后,我们用本文的观点看几个事例:
① 2是整数,4/2是分数。
② (x^2+1)/(x^2+1)是分式。
③ √[(a^2+1)^2]是二次根式。
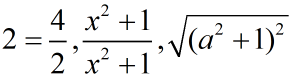
从概念上讲,2是整数,但4/2是假分数,虽然它们相等,但形式上是有区别的。同理,(x^2+1)/(x^2+1)符合分式的定义,所以是分式,√[(a^2+1)^2]符合二次根式的定义,所以是二次根式。
所以,回过头来,x=x+1,按照课本定义,含有未知数的等式,根据形式,它是一个方程,只不过是一个无解的方程,方程无解不等于就不是方程。但0=1是不是方程呢,当然不是,没有未知数,虽然x=x+1等价于0=1,但从形式上来说,他们的概念是不一样的。所以这些都要
根据课本来,不能不看课本,自己想象。离开课本对概念的阐述来讨论问题没有意义
。
再比如下面这个例子,乍看之下好像没有破绽:

其实,是不是这样呢?当然不是,不然就得到-1=1的谬论了,教材上对√a·√b=√ab这个公式的说明早就备注了(沪教版八年级上册12页),也就是当根号里面是负数时,这个公式是不符合条件的

离开课本来讨论问题,就好比无根之木,是站不住脚的。所以要以课本为根本,为规矩。尤其是数学概念和定义,数学式子千变万化,本质也许都一样,但我们定义它,是根据课本规定的形式去定义的,写成2,就是整数,写成4/2,就是分数,写成x=x+1,就是方程,写成0=1,就不是方程,一码归一码,清晰明了,也没有牛角尖可钻
以上问题主要内容来源于【揽数习文群】的讨论,征得群主大罕老师的同意,将他的原创文章发布于此,文字有所增,添供君阅览,也欢迎大家讨论留言
【往期内容】
想,都是问题,做,才是答案
持之以恒,进步是自然
上海高考“3+3”考试及各高校专业选科要求
解读数学的意义
北大2017年开学典礼新生演讲



