允中 发自 凹非寺
量子位 报道 | 公众号 QbitAI
编者按:
提前“剧透”并不一定能提高自监督学习性能,这是华为诺亚实验室最新的理论研究结果。
由于自监督学习数据和下游任务完全独立,因此预训练结果不一定能保证在下游任务中的性能。那么,我们是否可以在自监督学习阶段引入下游数据,来更好地匹配下游任务呢?
华为诺亚实验室用理论方法证明:当下游数据较少时,不用下游数据训练的效果反而要比用下游数据训练的效果更好。
简介
自监督学习是目前人工智能领域大热的一个方向,图灵奖得主Yann Lecun和Yoshua Bengio都认为自监督学习是机器智能达到人类水平的关键。
自监督学习是用大量无标签数据训练一个特征提取器,然后应用到不同的下游任务中。

这种学习范式已经在各种CV和NLP等任务上超越了直接用监督学习的性能。但是用于预训练的数据和下游任务数据通常是独立的,因此自监督学习在理论上并不能保证下游任务的性能。
一个自然的想法是,如果我们把部分下游任务数据引入到预训练阶段来指导特征的学习,这种做法对自监督学习有帮助吗?
直觉告诉我们,在预训练阶段如果提前获取了下游任务的部分信息,这样应该能够提升自监督学习的性能。我们从理论上对此进行了分析,发现在一些情况下,引入下游任务数据不但不会提升反而还会损害自监督学习的性能。
本工作是业界比较早的关于自监督学习的理论工作。
论文地址:(点击底部左下角“阅读原文”可直接进入)https://arxiv.org/abs/2103.03568问题定义
自监督学习常见的实现方法有:基于生成模型(学习一个数据到表示的双射)、基于对比学习(最大化数据和表示的互信息)和基于pretext task(利用人类经验给数据打上标签)。在自然语言处理中,用基于pretexttask的自监督学习得到的模型(比如BERT)已经可以明显超过监督学习的性能。另一方面,最近的一些实验指出,pretext task的选择对于下游任务的性能至关重要,糟糕的pretext task会导致下游任务适配的失败。因此,本文想尝试从理论角度分析pretext task和下游任务的联系,并考虑当pretext task已经选取不佳的时候,能否通过引入部分下游任务的数据来指导pretext task的训练。
为了方便理解,先简单介绍一下什么是pretext task。比如下游任务是图片分类的话,那么输入样本是一张图片,而预训练用的数据就是无标签的图片。对任意一张无标签的图片(比如头朝上的鸟),我们可以把它旋转0,90,180,270度得到四张图片,然后给这四张图片打上0,1,2,3的标签(pretext label),这样pretext task就是一个预测图片旋转角度的四分类问题,而这四张图片如果放到下游任务,对应的下游任务标签就是“鸟”。
最近有一个工作(Lee et al., 2020)指出,基于pretext task的自监督学习可以降低下游任务的采样复杂度(sample complexity)。具体来说,如果用x,y,z分别代表输入样本,下游任务标签和pretext label,当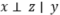 时,自监督学习的下游任务采样复杂度可以被显著降低。比如对于高斯变量的话,复杂度可以从
时,自监督学习的下游任务采样复杂度可以被显著降低。比如对于高斯变量的话,复杂度可以从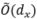 降到
降到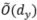 ,其中前者是直接用监督学习的采样复杂度,d代表下标变量的维数;而当条件独立性不满足时,采样复杂度会变坏到
,其中前者是直接用监督学习的采样复杂度,d代表下标变量的维数;而当条件独立性不满足时,采样复杂度会变坏到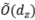 。这是由于大量的冗余信息(跟下游任务不相关的信息)在预训练时被引入到了表示中,在下游任务训练时,这些冗余信息到下游任务标签的映射关系也要被学习,因此增大了采样复杂度。在实际应用中,条件独立性基本不能满足,这样自监督学习的潜能就无法被充分发挥出来。(Lee et al, 2020)在文中建议使用PCA降维来剔除冗余信息,但是简单地用PCA降维无法保证跟下游任务相关的信息不会被误剔除,从而导致泛化误差恒大于一个常数。当条件独立性不满足的时候,如果我们能够设计一个函数f使得
。这是由于大量的冗余信息(跟下游任务不相关的信息)在预训练时被引入到了表示中,在下游任务训练时,这些冗余信息到下游任务标签的映射关系也要被学习,因此增大了采样复杂度。在实际应用中,条件独立性基本不能满足,这样自监督学习的潜能就无法被充分发挥出来。(Lee et al, 2020)在文中建议使用PCA降维来剔除冗余信息,但是简单地用PCA降维无法保证跟下游任务相关的信息不会被误剔除,从而导致泛化误差恒大于一个常数。当条件独立性不满足的时候,如果我们能够设计一个函数f使得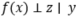 ,这样我们就可以用
,这样我们就可以用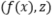 数据对来学习表示,从而仍能达到最优的下游任务采样复杂度。通过函数f,我们可以剔除x中的冗余信息,如上图所示。由于条件独立性依赖于下游标签y,因此我们需要部分下游任务数据来得到f。如果用算法来实现上述想法,见下图。其中算法1是标准的基于pretext task的自监督学习流程,算法2是引入下游数据来学习函数f的自监督学习的流程,其中算法2的3-5步对应于算法1的1-3步。为了更加直观的理解算法2,我们考虑一个简单的例子。给定x,假设y和z分别等于x的前
数据对来学习表示,从而仍能达到最优的下游任务采样复杂度。通过函数f,我们可以剔除x中的冗余信息,如上图所示。由于条件独立性依赖于下游标签y,因此我们需要部分下游任务数据来得到f。如果用算法来实现上述想法,见下图。其中算法1是标准的基于pretext task的自监督学习流程,算法2是引入下游数据来学习函数f的自监督学习的流程,其中算法2的3-5步对应于算法1的1-3步。为了更加直观的理解算法2,我们考虑一个简单的例子。给定x,假设y和z分别等于x的前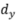 维和前
维和前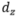 维(见下图),此时条件独立性不满足。标准自监督算法1学到的表示中会含有
维(见下图),此时条件独立性不满足。标准自监督算法1学到的表示中会含有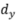 维的有效信息和
维的有效信息和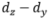 维的冗余信息,因此我们需要
维的冗余信息,因此我们需要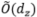 个样本去训下游回归器。相比之下,算法2先用函数f把
个样本去训下游回归器。相比之下,算法2先用函数f把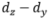 维的冗余信息剔除,这样学到的表示中只含
维的冗余信息剔除,这样学到的表示中只含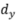 维有效信息,这样下游任务采样复杂度就可以降到
维有效信息,这样下游任务采样复杂度就可以降到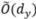 。根据上面的理解,我们的问题就变成了寻找满足要求的函数f。如果只有
。根据上面的理解,我们的问题就变成了寻找满足要求的函数f。如果只有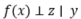 一条的话,会导致学到平凡解:比如f(x)是个随机噪声,就能满足条件独立性,但是没有意义。因此,我们还需要保证f加到x上之后,不会丢失对y的预测能力。我们总结成函数f需要同时满足如下两个条件(其中
一条的话,会导致学到平凡解:比如f(x)是个随机噪声,就能满足条件独立性,但是没有意义。因此,我们还需要保证f加到x上之后,不会丢失对y的预测能力。我们总结成函数f需要同时满足如下两个条件(其中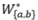 代表用b预测a的最优回归器):
代表用b预测a的最优回归器):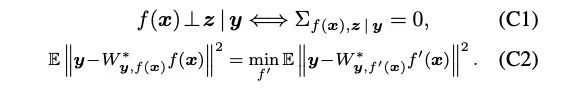
如何学函数f
条件(C1)要求f(x)和z要条件独立,换句话说,f(x)要尽量不能预测出z,于是我们要最小化同时,条件(C2)要求f(x)保留预测y的能力,于是我们要最小化可以证明,通过优化上述损失函数能学到同时满足(C1)和(C2)的函数f,如下:上述定理的证明思路:损失函数可以重新拆分成两项之和,其中一项正比于,而另一项达到最小当且仅当条件(C1)成立。理论结果
这节主要分析需要多少下游数据才能学到满足要求的函数f,因此我们假设我们拥有无限的无标签数据(x,z)。如果无标签数据不是无限,那么需要的下游数据会更多。于是,training loss可以写成:
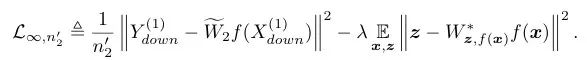
可以证明,在合理的假设条件下,至少需要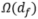 个下游数据才能学到满足要求的函数f:
个下游数据才能学到满足要求的函数f:
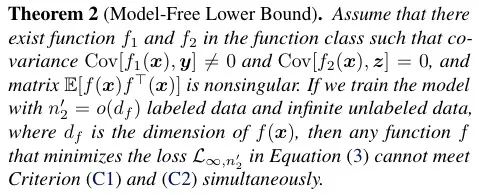
上述定理表明,当下游数据较少时(比如小样本任务),不用下游数据训练的效果反而要比用下游数据训练的效果更好。
这里的结论是基于第 3 节中提出的损失函数来分析的,读者可能会产生疑问,上述结论是否只限于这种损失函数才成立呢?为此,我们进一步分析了更加一般的损失函数。由于有标签数据和无标签数据分别来自不同的数据集,因此一般的损失函数应当包含有两项,一项是关于有标签数据的,另一项是关于无标签数据的。同时,一个合理的损失函数应当尽量能够拟合下游数据同时尽量不要拟合无标签数据中的冗余信息。所以,我们定义一般的损失函数如下: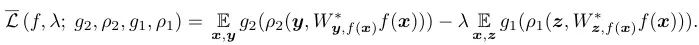
此处的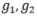 是单调递增的函数,
是单调递增的函数,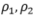 是距离度量。当他们分别取平方函数和欧式距离的时候,上述损失函数退化为第3节中提出的损失函数。可以证明,在合理的假设条件下,仍然至少需要
是距离度量。当他们分别取平方函数和欧式距离的时候,上述损失函数退化为第3节中提出的损失函数。可以证明,在合理的假设条件下,仍然至少需要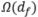 个下游数据才能学到满足要求的函数f(具体细节参见原文)。
个下游数据才能学到满足要求的函数f(具体细节参见原文)。
更进一步,如果把模型的结构考虑进来,我们可以把结论更加细化。我们首先定义模型容量如下:

直观来说,模型容量刻画了在有限样本下,函数空间拟合随机变量的能力,有点类似回归问题下的 VC 维。比方说,在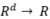 的线性函数空间下考虑L2损失,那么对应的模型容量就是d。这是因为当样本数n
的线性函数空间下考虑L2损失,那么对应的模型容量就是d。这是因为当样本数n有了模型容量的定义,我们可以用它来给出模型结构依赖的样本数下界:
实验验证
我们用标准高斯分布生成100维的向量作为x,取x的前80维并加上幅度为0.01的标准高斯噪声作为pretext label z,取x的前5维并加上幅度为0.01的标准高斯噪声作为 downstream label y。训练数据由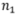 对(x,z)和对
对(x,z)和对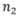 (x,y)构成,测试数据在训练数据之外采样生成。标准自监督学习(算法1)使用
(x,y)构成,测试数据在训练数据之外采样生成。标准自监督学习(算法1)使用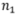 对(x,z) 做预训练,
对(x,z) 做预训练,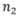 对(x,y)做下游任务训练;算法2使用
对(x,y)做下游任务训练;算法2使用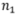 对(x,z)和对
对(x,z)和对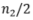 (x,y)做预训练,另外
(x,y)做预训练,另外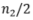 对(x,y)做下游任务训练。
对(x,y)做下游任务训练。损失函数的合理性
我们固定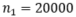 为一个很大的数,通过变化
为一个很大的数,通过变化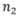 来观测下游任务在测试集上的表现。从图(a)中看到,随着样本数的增加,下游任务的表现越来越好,最终MSE趋于零,这和理论上分析的损失函数的合理性一致。同时,这个实验也指出,我们的方法在各种样本数目下都比标准自监督要更好。另外,其中当
来观测下游任务在测试集上的表现。从图(a)中看到,随着样本数的增加,下游任务的表现越来越好,最终MSE趋于零,这和理论上分析的损失函数的合理性一致。同时,这个实验也指出,我们的方法在各种样本数目下都比标准自监督要更好。另外,其中当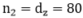 时,标准自监督出现一个尖峰,这是 Double Descent 现象。
时,标准自监督出现一个尖峰,这是 Double Descent 现象。
损失函数系数的影响
由于定理1在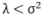 时成立,所以我们预期较大的
时成立,所以我们预期较大的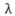 会影响算法的性能。我们从图(b)中观测到当
会影响算法的性能。我们从图(b)中观测到当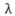 较小时,算法2表现出色;而当
较小时,算法2表现出色;而当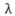 较大时,算法2的表现不及算法1,这说明此时已经无法学到合适的函数f了,学到的函数f已经误剔除了部分y的信息。
较大时,算法2的表现不及算法1,这说明此时已经无法学到合适的函数f了,学到的函数f已经误剔除了部分y的信息。
函数f的维数影响
定理2指出下游数据量的下界是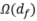 ,所以在下游数据量固定的情况下,我们预期随着
,所以在下游数据量固定的情况下,我们预期随着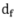 的增加,算法的性能会下降。图(c)中观测到当
的增加,算法的性能会下降。图(c)中观测到当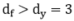 时,算法2的性能开始不及算法1。
时,算法2的性能开始不及算法1。
根据上述这些实验,我们可以得出,算法2确实能够提升自监督学习的性能,但是当下游数据较少时,引入下游数据训练反而会让自监督学习性能变差。同时,全部的实验结果都与我们的理论预测一致。
我们团队目前主要从事机器学习理论的相关研究,欢迎有兴趣加入我们的同学发送简历至 weiran.huang AT huawei.com1. Teng, J*, and Huang, W*. Can Pretext-Based Self-Supervised Learning Be Boosted by Downstream Data? A Theoretical Analysis, arXiv:2103.03568, 2021.https://arxiv.org/abs/2103.035682. Lee, J. D., Lei, Q., Saunshi, N., and Zhuo, J. Predicting what you already know helps: Provable self-supervised learning. arXiv preprint arXiv:2008.01064, 2020.https://arxiv.org/abs/2008.01064— 完 —
本文系网易新闻•网易号特色内容激励计划签约账号【量子位】原创内容,未经账号授权,禁止随意转载。
点这里👇关注我,记得标星,么么哒~
量子位「AI社群」招募中!欢迎AI从业者、关注AI行业的小伙伴们扫码加入,与50000+名好友共同关注人工智能行业发展&技术进展:
一键三连「分享」、「点赞」和「在看」
科技前沿进展日日相见~















