
本文由微信公众号“科研圈”(ID:keyanquan)授权转载
转载请先联系[email protected]

天然贝壳(左)与仿制贝壳(右)。图片来源:Meinhardt, H. (1995). The Algorithmic Beauty of Sea Shells. Springer Verlag. pp.179
如果你的电脑里出现了能够自我复制的东西,你的第一反应是什么?病毒?其实,除了电脑病毒以外,还有一种东西也能够自我复制。这种数字生物生活在一个二维的方格世界里,这个世界叫做“生命游戏”。
普林斯顿的哥特式大楼外挂满了常春藤,这些庄严的建筑看起来和约翰·何顿·康威(John Horton Conway)这位老顽童不太相称。康威是个不修边幅的老头子,气度超凡绝尘,有点像《魔戒》中霍比特人比尔博·巴金斯和白巫师甘道夫的混合体。
康威用他那口英式老牙啃着左手食指的指甲,额头上的青筋突出,棕色的眉毛因为思绪而紧缩着,他的头发看起来从前天起就没有打理过。他就坐在那儿,毫无愧疚地把大把的时间拿来“思考”。不过他却坚称,自己什么都没干,只是在玩游戏而已。

康威在玩生命游戏,摄于1974年。图片来源:THE SUN NEWS SYNDICATION
79岁的康威目前是普林斯顿大学应用于计算数学的荣誉教授,他已入选英国皇家学会,海内皆恭维他是个天才。不过他的名声是在英国剑桥大学获得的。他说他这辈子哪怕连一天也没有工作过,一直都在玩游戏。你要是去数学系三楼的公共休息室,八成能看到他在那里闲逛。
康威为数学经典做出的最大贡献是他设计的数不清的游戏。其中最著名的就是他在60年代末设计的“生命游戏”(Game of Life)。《科学美国人》(Scientific American)的专栏作家马丁·加德纳(Martin Gardner)管它叫“康威最著名的作品”。
它可不是一款普通游戏,而是一种元胞自动机。
元胞自动机是由一群细胞构成的小机器,它是根据一些简单规则和初始图形进行演化的动力系统。这些细胞在离散的时间中不断演化——每一代所有细胞都同时经历一次变化。最终这些细胞的集合看起来就像变形金刚一样在不断改变形态,甚至和显微镜下的蠕动的微生物有几分相似。

康威(左)和冯·诺依曼(右)
元胞自动机的计算机框架大多是图灵在30年代奠定的,但是首要工作是约翰·冯·诺伊曼(John von Neumann)在40年代完成的。冯·诺伊曼设计元胞自动机的初衷就是为自然界的自我复制和生物发展提供一个简化理论。冯·诺伊曼最初设计的是一个离散的二维系统。他的元胞自动机也是首个可被称为通用计算机的离散并行计算模型。
元胞自动机对于生物现象的最大影射在于,生命的起源更像是一种相变,而进化则像是秩序和混沌之间的挣扎。冯·诺伊曼的追随者们感到它对生命的解释有着非凡的意义。在这个大背景下,康威在1970年提出了元胞自动机的最佳样本——
在严格意义上,生命游戏并不是一种游戏,因为在这个游戏里没有任何玩家。康威说它是一种“0玩家且永不结束”的游戏。
纪录片《史蒂芬·霍金之大设计》(Stephen Hawking’s Grand Design)曾经这样介绍它:“像生命游戏这样规则简单的东西能够创造出高度复杂的特征,智慧甚至可能从中诞生。这个游戏需要数百万的格子,但是这并没什么奇怪的,我们的脑中就有数千亿的细胞。”
和冯·诺伊曼采用的含有29个不同的状态的复杂的动力系统不同,康威设定的基因定律简单而优美。其基本思想是:
棋盘代表了一个世界,这个世界的空间是无限的;
每个格子里最多可以生长一个细胞(生命体);
每个细胞与周边九宫格内8个细胞相邻,其中4个处在上下左右,另外4个处在对角的位置;
这些初始生命体会一代代地生长、死亡和繁衍。
康威在挑选这些基本规则的时候花了很大的力气,还进行了很长时间的实验。他的目的是让整个群体的行为变得无法预测。他规定细胞的生死或繁衍的规则如下:
生:与2或3个细胞相邻的细胞将活到下一轮;

死:与4个及以上细胞相邻,则因为过度拥挤而死;与1个或0个细胞相邻,则因为孤独而死;
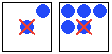
繁衍:一个空格若与3个细胞相邻,则在下一轮时,这个空格内将产生一个新细胞。
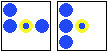
在每一代中,生死、繁衍都是同时发生的。每一代的细胞构成了一个群体,或者说“生命历史”中的一小步。
如果你自己试几轮,你就会发现初始图案会不断的变化,这些变化常常是意想不到的。有时候,看似很复杂的初始图案在经历许多轮之后会全部消失,或者说灭绝(burn out)。

有些初始图案最终会得到稳定不变的图形,康威把这些稳定图形叫做“静物”(still life)。常见的静物有:方块、小船、面包、蜂巢等(蜂巢是许多初始图案最终的样子)。
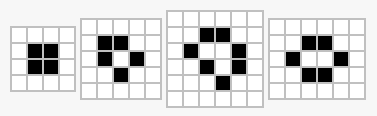
左起:方块、小船、面包、蜂巢。
康威的最大发现是“滑翔机”(glider,康威认为滑翔机属于轻量级的“太空船”spaceship,太空船是会不断移动位置,但会周期性回到原来样子的图案)。在2轮后,它会移动位置并且沿着对角线翻转。几何学家把这种反转叫做“滑移反射”(glide reflection),这就是为什么它被叫做滑翔机的原因。再过2轮,滑翔机又会翻回来,并沿着对角线向下移动1格。

滑翔机、轻型太空船
实际上,滑翔机和太空船是能够传输信息的。理论上,可以用滑翔机来运行所有现代计算机能够执行的逻辑运算。已经有人用生命游戏制造出了能够输出素数的特殊计算机。
下面三幅图被称为“振荡器”(oscillator),因为它会在几个图案间不停轮换。康威把最简单的振荡器叫做“闪光灯”(blinker,下图左)。除了闪光灯,常见振荡器还有“信号灯”(traffic light,下图中,也是常见图案)和“脉冲星”(pulser,下图右)等。



闪光灯、信号灯、脉冲星
有一种5个细胞组成的图案叫做“R pentomino”。康威在试验了460轮后它依然没有灭绝,而且还从第69轮吐出一些“滑翔机”。
康威说:“它会留下许多奇奇怪怪的垃圾,它们四处游荡。不过它只有很少一部分活跃的区域,所以并不清楚它会不会一直如此无穷地持续下去。”实际上,后来人们发现 R pentomino 在第1103轮会最终稳定下来,此时它是由116个细胞组成的,它们组成了8个方块、6个滑翔机、4个蜂巢、4个闪光灯、1个小船、1个面包和1个大船(ship)。

初始状态和1103轮后的 R pentomino(不包括6个飞走的滑翔机)。图片来源:conwaylife.com
康威曾推测,没有任何图案能够无止境地生长。他曾拿出50美金作为奖品,奖励第一个能够在那年证明这个命题或者将其证伪的人。
这个奖在同年11月就被麻省理工学院的 Bill Gosper 摘取。Gosper 发现了“Gosper glider gun”,它在15轮产生第一个滑翔机,再过15轮又产生第二个滑翔机。这一模型是目前为止最小的 glider gun。
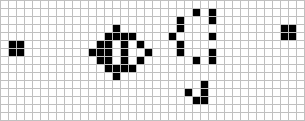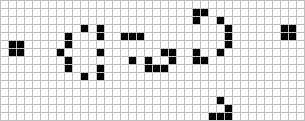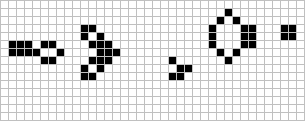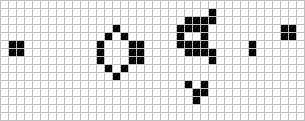
Gosper glider gun
实际上,“枪”(gun,能够不断产生移动图案的初始图案),或者“喷气火车”(puffer train,会移动的图案,在身后会留下一缕“烟”)也是能无限生长的初始图案。
后来,更多的枪、喷气火车和耙子(rake,能够移动并产生太空船)被发现。Gosper 还建造了第一个具有渐近最优二次增长速率的初始图案——“繁殖者”(breeder,也称“龙虾” lobster),它在行进的过程中会在身后留下一串“枪”。最后一种叫做“填充者” (Spacefiller),它会不断生长填充空间,这种图案是在1993年借助计算机发现的。

繁殖者

填充者
2010年,加拿大多伦多的程序员创造出了生命游戏中首个能够实现自我复制的图案——双生子(gemini)。(其实类似的能够自我复制的元胞自动机早已存在。比如,有一个著名的一维元胞自动机叫做“rule 90”,它可以在一定轮数后开始复制。)
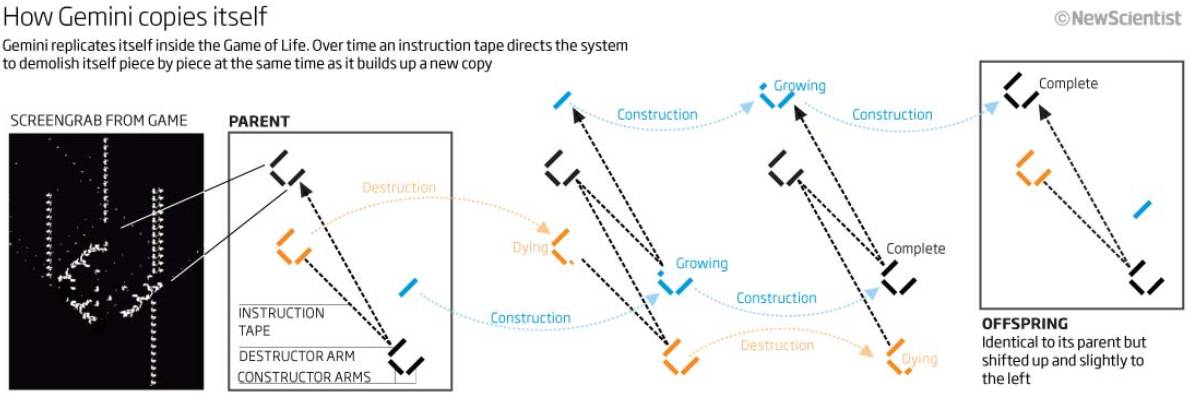
“双生子”自我复制的方式。图片来源:NewScientist
康威提出,图案移动到空白空间的速度是有限的。在方格世界中,速度的定义指的是,一个图案复制一次所移动的格子数除以轮数得出的值。
康威把1轮1格(可直角,可斜角移动;也就是国际象棋中王的移动速度)的速度叫做“光速”。康威把这个速度叫做“光速”的原因是,在方格世界中任何图案都无法超过这个速度。比如,滑翔机每4轮就复制一次并沿着对角移动1格,因此它的速度就是1/4光速。
康威证明,沿着对角线移动的最快速度是“光速”的四分之一,而太空船的最高速度是1/2光速,因为无法建造一个每一轮都能移动的太空船。不过在生命游戏中,可以通过介质获得光速,比如物体在穿越由蜂巢构成的特殊轨道时就能够以光速行进。有时候,物体看起来的移动速度超过了光速,不过这些都是视错觉。

“星际之门”(star gate)中的太空船在6轮中似乎“飞跃”了11格。图片来源:ericweisstein.com
康威曾经说:“坐在电脑屏幕前观看这些图案的变化真是不可思议的事。”他一语成偈——生命游戏是世界上被玩得最多的电脑游戏之一。
生命游戏的风靡正赶上新一代微型电脑的出现。当时有很多人让电脑在晚上空闲的时候运行生命游戏。美国军方的一份报告称,因为在工作时间偷偷观察生命游戏而造成的损失总计高达数百万美元。还有一份报告称,在70年代生命游戏风靡的时候,全世界大约有1/4的电脑都在运行这个游戏。从某种意义上讲,生命游戏甚至引领了后来计算机生成的分形的热潮。
生命游戏中扭曲变形的图案的对于许多研究数学、物理和计算机科学的学生以及爱好者而言具有致命的吸引力,生命游戏的疯狂追随者把这个游戏当成了珍贵的消遣。从70年代起,生命游戏就吸引了一群狂热信徒,他们用生命游戏创造出了各式各样的模式,甚至有人在生命游戏中创造出了计算机系统的理论仿真模型。
生命游戏直接推动复杂性科学将元胞自动机和个体为本模型(agent-based simulation)融合进来。类似生命游戏的二维元胞自动机能够展现于多物理、生物甚至人类的现象,比如完全气体的动态、风暴中鸟类的运动、战场上士兵的排兵布阵等等。
在游戏玩家中,生命游戏也享有盛誉。因为生命游戏对于由个体组成的社会的兴衰变化有着恰当的比喻,这直接促成了一类被称为“模拟游戏”(simulation game)的新式玩法。
而对另一些人来说,生命游戏还有着更不可思议的宗教、哲学含义:在没有设计者的情况下,“设计”和“组织”也会自发出现。
后来人们了解到,生命游戏便是“涌现复杂性”(emergent complexity)或者说“自组织系统”(self-organizing system)的最简单版本。通过生命游戏,人们可以理解复杂的模式和行为是如何从几条简单的规则中“涌现”出来的。比如,它可以解释,玫瑰的花瓣或者斑马身上的条纹是如何从一些生长在一起的活细胞中演变出来的。它甚至能够帮助我们理解生命复杂性的来源。认知科学家、哲学家丹尼尔·丹尼特(Daniel C. Dennett)甚至提出,康威生命游戏说明,复杂的哲学建构,比如意识和自由意志可能就是由一些简单的物理定律触发的,而这一切本质上是决定论的。

贝壳每次长一层细胞(类似于指甲),这个生长的过程就是一个一维元胞自动机。图片来源:Meinhardt, H. (1995). The Algorithmic Beauty of Sea Shells. Springer Verlag. pp.179
加德纳曾说,生命游戏让康威一夜成名。
康威一直在纯数学领域进行研究。当康威的虚荣心作祟的时候,他就会打开一本新出版的数学书,然后在书的索引中查找自己的名字。然而他的名字常常作为生命游戏的作者而被引用,这让他很懊恼。因为,其实他对数学的贡献广泛而深远。
他在1967年发现了一种新的群——康威群(Conway's constellation)——在数学对称性海洋中的三个散在群(sporadic group,不符合任何分类规则的群)。除了2个散在群以外,康威群几乎包含了当时已知的所有散在群。他的这项突破性研究让从事有限群以及数论的数学家都大受震动。
他还对怪兽月光猜想(Monstrous Moonshine)中散在群中的最大一支——魔鬼群(Monster group)进行了深度研究。
他认为自己对数学最大的贡献是发现了一类新型的数——超现实数(surreal numbers)。超现实数系统是一种连续统,其中含有实数以及无穷大和无穷小。超现实数可能能够解释宇宙的波澜壮阔和量子的秋毫之末。
然而,他认为自己有如此多兴味恰恰说明自身是浅薄的。
康威把自身放在数学这座古老大厦的何处呢?他有时把自己比作在时间的街道上,一支笙鼓齐鸣的行进乐队中的一员。
除非有人刻意提起,他其实很少考虑自己在数学名人堂中的地位。世界最老的周日报刊《观察家报》(the Observer)将康威列入改变了世界的数学先贤祠中。对此,他颇为不屑:
“他们这样想让我感觉不错。这意味着我可能是在世的最优秀的数学家之一。但这和最优秀的数学家是有差别的。我的名气可能来自于生命游戏。这让我不舒服,因为人们认为我是创造它的人。我可以保证我不是最优秀的数学家,因为至少这些优秀数学家榜单并没有把阿基米德和牛顿列进去。”
康威认为自己的一生都是在游戏中度过的,而他钟爱的游戏也给了他最诚挚的回馈。对于游戏和消遣,他给后生们提出了这样一则忠告:
无患无疚,毋宁逍遥。
Thou shalt stop worrying and feeling guilty
Thou shalt do whatever thou pleasest

烟花。图片来源:basilisk.fr
参考资料:
Gardner, M. "The Fantastic Combinations of John Conways New Solitaire Games." Mathematical Games (1970).
Berlekamp, Conway, and Guy: Winning Ways (for your Mathematical Plays), Volume 2, (c)1982. ISBN 0-12-091152-3.
Gardner, Martin: Wheels, Life, and Other Mathematical Amusements, (c)1983. ISBN 0-7167-1589-9.
Dennett, D.C. (2003). Freedom Evolves. New York: Penguin Books. ISBN 0142003840
conwaylife.com/wiki/Conway%27s_Game_of_Life
en.wikipedia.org/wiki/Speed_of_light_(cellular_automaton)
www.wired.com/2015/09/life-games-playful-genius-john-conway/
www.martin-gardner.org/SciAm1.html
en.wikipedia.org/wiki/Life-like_cellular_automaton
en.wikipedia.org/wiki/Conway's_Game_of_Life
www.newscientist.com/article/mg20627653.800-first-replicating-creature-spawned-in-life-simulator/
http://web.stanford.edu/~cdebs/GameOfLife/
无特殊注明的图片均来源于http://web.stanford.edu/~cdebs/GameOfLife/,读者可移步该网站体验“生命游戏”。(建议 PC 端体验)
编辑:J.C
本文由微信公众号“科研圈”(ID:keyanquan)授权转载。
转载请先联系[email protected]。
近期热门文章Top10
↓ 点击标题即可查看 ↓
1. 通往物理学世界的地图
2. 史上最难逻辑题!据说99.9%的人都做不出来……
3. 学校教给你的N个谎言
4. 不能说的秘密:薛定谔方程是怎么推导出来的
5. 你好,我在10维时空等你
6. 正经向 | 葫芦娃中的那些“黑科技”
7. 圣诞老人的真面目
8. 妹子办公室进老鼠了,能忍?
9. 十个问题带你认识弦理论!
10. 物质本身有颜色吗?
点此查看以往全部热门文章
















