作者:曾庆存 (中国科学院大气物理研究所)
6.1 模式的理性检验——数学物理基础问题
大气作为连续介质的流体,其动力学方程的每一项都是就每一个数学上的点而写出的,并且还做了一定的近似。这就产生了许多问题,例如单从这些偏微分方程出发,大气的整体是不是满足质量守恒、能量守恒和角动量守恒等定律?内能与动能和位能是怎样相互转换的?热机的效率如何?所引入的近似,如薄层近似(大气的有效厚度与地球半径相比非常小,在大气中各点离地心的距离可近似视为等于地球半径——如它以系数的形式出现在方程中的话),表观重力近似(重力加惯性离心力取为常数,且垂直于球面)和准静力平衡近似(忽略了惯性力中的垂直分量)等,是否在整体上破坏了物理原则,或只改变了能量、角动量等的表达式?引入的近似是不是相容的或自洽的?大气有底界而无上界(在数学上讲是在无穷远处),边界条件应怎样提才是正确的和符合物理原则的?初始条件该怎样提法?等等。作为预报问题应怎样提才是物理上合理的且数学上也是严谨的和适定的?即是否有解,解是否唯一,和对初边值条件是否连续依赖?这些都是基础问题。我们不能满足于数值预报的一时胜利,而应就上述这些问题进行理性的检验,对离散化了的计算格式更应如此,这样才能把数值预报建立在坚实的严格数学物理基础之上,才能健康地发展。其实,在以往的某些个别的具体数值预报模式中,不乏有在整体上破坏物理原则的和不自洽的,甚至无解的或多解的。
笔者在实际工作中注意了这些问题,进行了长期研究,大部分问题大体上已给出了解答。自上世纪80 年代中期起,在国内外已有许多进行理论研究的大气科学家、地球流体力学(即大气和海洋动力学的共性问题)学家投身研究,为原始方程模式的具体形式打好了可靠的数理基础,但有些很抽象的理论问题还有待解决。
其次,大气运动演变的基本规律也得弄清,以便认识为何有些天气过程能预报得好,而另一些则预报得不好。例如大气中有各种尺度运动的相互作用,大气绕地轴旋转的环流称为带状环流(或基流),迭加于其上的就叫做扰动,包括大气长波和天气系统。在什么条件下和有什么样结构的扰动是发展的?什么样的条件和什么样结构的扰动是衰减的?等等,这些都是基本规律性的基础研究问题。
6.2 非绝热(adiabatic)物理过程
6.2.1 水汽相变和云雨(雪)物理过程的复杂性
水汽在空中凝结变成云滴(水滴、雪花、冰晶),释放出大量潜热,直接加热当地大气,并通过扩散混合和对流运动等进一步加热周围的大气;而当云滴增大后由空中下降至地面,并不把已释放的热量带走,除非它在空气中又蒸发成水汽。在自然界大气中,不比在物理实验室中,凝结是在自然界尚未很好认识的凝结核和云滴表面上发生的,影响的因素很多,非常复杂,就连饱和水汽压与温度的关系也不能完全依赖热力学理论推出,其中包含了不少经验的修正和经验常数。尽管如此,尚可以半理论半经验地将水汽相变过程引入模式之中,以计算其对大气运动场(天气系统)的影响,但因其复杂性,公式有待进一步改善。
由云滴增长到雨雪形式以及形成降水的过程更为复杂,还须考虑凝结、蒸发以及粒子在湍流、重力和电场作用下的碰并,在云中还有更复杂而尚不大清楚的过冷却水滴的存在以及它与冰晶相互作用的过程,这些均是物理学研究的对象。在大气科学界中到目前也只能粗略考虑这些因素,故至今尚难准确预报降水量。
6.2.2 辐射传输过程和云与辐射相互作用的复杂性
大气对太阳光有散射和吸收作用,这些都可以用物理学的散射理论和量子力学进行计算,而对悬浮在大气中的粗粒子(包括云滴)的作用的计算则相当复杂,较密厚的云顶甚至可视为反射面。大气对红外辐射的吸收和发射的计算就更为复杂得多。就以纯粹的大气气体成分来说,例如CO2和水汽(H2O)对红外辐射的吸收是由众多的吸收谱线造成的,要对每条吸收线逐一进行积分才能得到一个谱带(仍然是很狭小的)的吸收,甚至是用现代的超级计算机来计算也是非常耗时的。大气科学界现在采用两种方法解决:一种是利用谱带吸收的实验资料拟合的公式;另一种是将吸收线吸收沿透过系数进行重整,将沿频率的黎曼积分变换成沿透过率的勒贝格积分。尤其是后者,既大为省时,又有相当好的精度(理论上说是完全精确的),也是一个将物理问题和数学方法很好结合的典型例子。
难办的是大气中粗粒子(即所谓气溶胶,aerosol)和云雨的存在,它们的化学成分复杂,又与辐射有很复杂的相互作用。辐射作用使它们的微物理特性(如凝结率、粒径及其谱分布)发生改变,而这又反过来影响辐射传输过程本身。这些是直到目前数值天气预报和气候预测中最不确定的问题,尤其是当云等为空间不均匀的情况时。
6.3 次网格尺度过程和参数化方法
进行数值计算总要离散化,于是在空间上总有一个可表达的最小尺度,俗称网格距(grid size)。小于网格距的过程称为次网格尺度过程(subgrid processes),它们本来在计算模式中是没有的,但在实际大气中是客观存在的,而且多种多样,做天气预报时不能不考虑;它们甚至对模式中可表达的尺度过程(天气系统,或简称大尺度过程)还有强烈作用,故在数值天气预报中必须进一步考虑这一点。为此,就得使用参数化方法(parameterization),即通过物理考虑(甚至是经验),将次网格过程的特性及其对大尺度过程的影响用大尺度的状态变量来表达,得到一些公式,其中包括一些参数。下面举两个有名的例子。
6.3.1 积云对流参数化
在很多情况下,降水往往是由积云对流(cumulus convection)产生的,而一朵积云的水平尺度为几公里到几十公里,即使在现代的数值天气预报模式中都无法很好表达,因此需要参数化处理。有两种典型的方法:郭晓岚(Kuo H. L.)方法和荒川(Arakama A)方法。目前使用的是它们的细化改进或混合改进。
这些参数化方法都将大尺度大气变量看作在水平方向是均一的,只有垂直结构。小尺度扰动在这种环境中发生,特别是因地面不均匀,总有气块上升,若环境合适(即达到对流发展的判据),使其所受到的浮力大于其自身的重力时,气块就能继续上升而温度降低,达到一定高度后,其中的水汽就会凝结成云,释放的潜热使气块温度升高而更易上升,释放更多的热量,最终使网格内的大气加热。设定扰动的类型(云体形态)和取某种统计分布,就可算得网格内积云对流加热率的垂直分布。郭晓岚方法设云为云泡,内部均匀,成云降水的总量由大气最底层的水汽辐合量决定,不必考虑云尺寸的分布,由此得到的加热率垂直廓线很简明,即其参数化公式主要由“水汽辐合量”这个参数决定。荒川方法则设每朵云是互相独立的,都有相似的结构,其水平尺寸有谱分布,决定于云底的风速辐合量。假设云的发展在瞬间即达平衡态,由此决定谱形,对云谱积分就可算出加热率曲线。这种参数化方法看似更仔细,但仅是有相似的云形这点就与实际不符。所以两种方法都留有很大的改进空间,但无论如何,都使在数值天气预报中计入积云的影响成为可能而被大量应用。
6.3.2 不均匀云与辐射的相互作用参数化
大气中的云种类繁多,按其出现的高度分,有低层云、中层云和高层云;按其状貌来分,有积状云、层状云、浅薄的卷状云以及三者的混合,它们的微物理特性各不相同,对辐射传输的影响也各异。严重的是,它们在一个网格内很不均匀,沿高度又可能相互重叠。它们对辐射的影响不是相互独立的,例如,当太阳光垂直下照时,要先经过上层云的削弱,才能达到下面一层云的顶部,经它的削弱后再向下传输,这种影响是以乘积的形式出现的。但我们无法确知次网格的云在三度空间中的分布,故要计算一个网格上的辐射量,必须按某种物理的或纯粹计算上的考虑,对云分布的几何学和微物理特性做种种统计考虑,从而得到次网格云与辐射相互作用的参数化方案,它由各种云的参数化、云的微物理特性参数化以及辐射传输计算的参数化方案等组成,十分复杂。大抵这样的次网格云与辐射相互作用的参数化方案就是几个非线性算子的乘积,不满足交换律和分配律,各家方案各有所长,计算得到的辐射值则有可观的差异。
于是人们尝试将各种参数化拆开,再进行重组,用统一的计算顺序和统一的编程,进行集合平均,结果是可以在相当程度上消去不确定度。此外,按此法还可找到合理且最优的参数化方法,目前正在全面探索之中。
6.3.3 大气边界层和下垫面的影响
大气的最低层就是所谓的边界层(boundary layer),它与地表面接触而产生一些特有的相互作用过程,影响着热量传输、水汽传输以及相变、动量传输和表面摩擦等过程。这些都会影响边界层上的大气运动,甚至会影响到一些剧烈的天气系统发展与否,例如海面的蒸发和水汽在边界层内的辐合量是台风形成与发展的重要过程,陆表上的对流和积云的生成亦大多由边界层内的扰动演变而成,而这些扰动则大多是由地形和陆表特性的不均匀所致。正如一般流体力学中边界层问题一样,大气边界层也只能半理论、半经验地将动量、能量、物质等的传输作为湍流扩散过程来处理。此外,如果地表特性的不均匀性与随机性相差很远,即可有次网格尺度的结构,则不能套用统计模式计算网格上边界层的通量等,而必须用小范围但具有更高分辨率的模式计算,如山谷风环流、海陆风环流等,然后再嵌入到原来的模式中。
6.4 可预报时限和预报能力
由于观测资料的不完备,且必有误差,模式又有各种各样的简化,其中的参数也有不确定性,再加上计算上的截断误差和舍入误差,这些必然会通过误差的累积过程(非常复杂而大多尚不可知晓)使预报越来越不准确,而最终使某时刻的预报不可信,这个时刻离始报时刻的时间长度就称为可预报时限。它是考察一种模式或一种预报方法的能力的一种指标,通称为预报能力(predictability)。这是很重要的实际问题。
就用模式做预报来说,可有两种方法确定可预报时限。一是在模式中引入随机误差,无论是引入到初始场中,还是引人到模式中所包含的诸多参数中,误差的标准方差(standard deviation)应等于实际的标准方差。于是预报场就是一个集合,研究其离散度随时间的变化,当它达到大气变量自身变化的方差时,这个时刻离初始时刻的时间长度就是可预报时限。此后的预报就是不可信的。另一种方法是根据已累积的预报个例的集合,计算预报和实况的离散度来定出可预报时限。最初人们是按第一种方法,所用的模式相当简单,得到了较乐观的估计,可预报时限为半个月。但后来,按第二种方法计算,即使到现在,可预报时限也只有7 天。其原因除模式的复杂性和观测的误差之外,也许还因为模式中还包含有未被我们认识的过程以及模式无法表达的天然不确定性或测不准之处,这些都是数值天气预报发展过程当中必须逐步研究解决的。
6.5 突变、分叉、混沌和韵律
无论是实际的天气过程还是数值天气预报,都发现有突变现象(abrupt change)和分叉现象(bifurcation),尽管不像数学上定义的纯粹突变和分叉那样。还有混沌现象(chaos),就是现在大家早已熟知的所谓“蝴蝶效应”,首先是由气象学家Lorenz通过非常简化的大气动力—热力学方程而发现的。Lorenz 的原话是,南方一只海鸥(并非蝴蝶)鸣叫会引来北方一场大雪。这当然是文艺的极度夸张譬喻,而非科学的真实。其实,海鸥(或蝴蝶)的动作只能引起它周边空气的极微小的运动,经过气体分子或湍流扩散,信号很快会在很小范围内消散殆尽。他只是以譬喻方式强调初值的误差会使预报差别很大,即中国战国时期的思想家早已指出的“差之毫厘,谬以千里”。后来,这个问题便用来讨论中期天气预报问题。
从统计意义上说,突变、分叉和混沌就是限制可预报时限的一些主要动力学过程,而就个例而言,它们都是很难预报的对象——如果未明了其动力学机理和规律的话,但它们的发生往往对应于剧烈的甚至形成重大灾害的天气。关于这些,正是天气学和数值天气预报应加以针对性研究的对象,理当别论。
天气和气候中还有所谓的“ 韵律” 现象(rhythm),例如,一种天气(或气候)形势在某地域某时段出现后,就会减弱甚至消失到无痕,可是经过一定时段之后,又会在原地域或别地域出现相似天气(或气候)形势。它主要是由动力学过程自身或模式结构自身所决定,初值误差的影响并不大。它在气候预测中尤其具有很重要意义,即寻找所谓的遥相关型(teleconnection pattern)。
突变、分叉和混沌现象,在经过初值误差决定的可预报时限之后,都可能产生韵律现象。但即使没有上述三者,也可以产生韵律现象。一个简单的物理例子是:两个频率相差不大的振动叠加起来,会产生一种被很低频率调制的群波传输出去,群波的包络线幅度就是一种韵律,它是动力过程自身所具有的特性。下面一个例子说明,并非在上小节定义的模式可预报时限之外,该模式就不具有预报能力。例如:对一个线性的简谐波f =cos(x-ct)来说,如果计算模式给出的相速为c+Δc,预报的波就是fp=cos(x-(c+Δc)t),预报误差为Δf = (fp - f ),它是t 的函数,如果取| Δf |第一次达到1/2 的时刻为可预报时限tp,则在tp之后,但在2π/Δc< t < 2π/Δc+ tp 之间,又有一段时间| Δf |≤1/2,也就是预报仍可满足要求。可见,如果人们有长时期的经验积累,不论是主观的,还是通过数值预报等总结出来的,只要善于总结,总可以参透玄机,悟其妙道,找到尽可能多的可以预报的天气和气候的类型。上节所定义的可预报时限和预报能力并非绝对的,天气的演变及其预报有许多奥妙呵。
7 大气环流模式的应用和集合预报方法——数值天气预报的成年
有了原始方程自洽的动力框架和合理的大气上下界边界条件之后,计入上节所述的物理过程,并将预报区域扩展到全球,数值天气预报模式就从物理和数学上说是理论严谨的了。不仅可以提高短期数值天气预报的精度,而且可以做全球范围和中期数值天气预报(即尽量达到自然的可预报时限)。所谓中期是指三天以上至一周或两周,而短期则指直到第三天。
1980 年前后,欧盟成立了中期天气预报中心(ECMWF),凝聚全欧科学家进行研究,并建立了日常业务,很快就发现数值预报中出现了本文第6.4 和6.5 节中提到的问题,并设想必须解决提高模式的精度问题(本文第6.2 和6.3 节)和碰到的与6.1 节有关的计算方法问题。上世纪90 年代,中期数值天气预报进入了成年期。
这里单讲提高可预报时限的一些问题。由观测资料得到的初始场中含有误差不可避免,但又不能确切知道其大小和分布。若模式足够好,则预报中所出现的巨大误差,尤其是由此引起的虚假的突变等现象,必定是由初始场中误差的某些有组织的结构及其演变所致。记误差场为δ (x,y,z,t),其范数为ε (t)(例如其全空间在t 时刻的能量)。显然,在初始时刻t=0 时, ε (0)就是初始场的观测误差的范数ε0 ,它等于观测误差的均方差。不难由模式推出误差场δ 随时间的演变方程,故在t 时刻范数最大的误差场就是在限制ε (0)= ε0 条件下, ε (t)为最大的那种结构δ (x,y,z,t),这可由数学运算求得(在数值预报情况下,当然要通过数值求解)。在上世纪90 年代初,Palmer 等最初设误差为小扰动,于是问题归结为求线性算子的一系列特征值和特征函数(在离散情况下为特征向量,Palmer 等称之为奇异向量(singular vector))。穆穆则进一步求解非线性扰动方程的特征向量。不难想象,这样的由奇异向量或特征向量表达的扰动在初始时刻必定是发展型的(否则不足以强大到改变原流场形态),但演变后期则可能变成衰减型(把能量反馈回已变形的基本流场),这正是本文6.1 节最后一段所指出的研究对象。将各个这样的向量( δn (x,y,z,0),n=1,2,…)加到初始场中去做预报,于是得到一个预报集合,取这个集合的数学期望作为正式的预报,这就叫做集合预报方法(ensemble forecast)。后来的实践表明,这样做确实既提高了预报准确度,也延长了模式的可预报时限。
8 四维同化方法和广义的初值问题——数值天气预报的成熟
将数值天气预报作为一个由初始场决定的初值问题,只用到了初始时刻的观测资料。其实我们有很多资料,也应该想办法在数值预报中应用起来,以提高预报精度和可预报时限。例如,我们还有卫星遥感、雷达观测、飞机观测、船舶观测、海上浮标观测等非定点定时的所谓非正规或非直接的观测资料。特别是随着预报的进行,还有不同时刻的观测资料逐次而来。而历史天气的某些有用的统计特性,则既可用来检验预报,更可以把这些检验结果作为订正,引入到预报模式和预报方案中去。这样的方法则不是狭义的初值问题,而是更实际、更有用的广义初值问题:从过去的经历预报未来,尽管这些经历在任何时刻都有误差,而且往往是不完全的。
这样,就发展出四维同化方法(4D data assimilation)。在有观测资料的三维子空间和时刻,使观测到的量和由模式直接算得的或间接推出的量相接近(融合),而没有观测资料的地域和时刻又有预报场作补充,于是在一定时段内就有一套更好更全面的混合而成的资料,故不断地随时有资料更新的预报必定比只用原来方法预报为好。欧洲中期天气数值预报就是这样做的,其预报是当今世界上最好的,其全球平均的可预报的时限已超过7 天,有望达到10天(图4)。这里可预报时限是取距平相关系数rop ≥0.5 的时段,rop是指气象变量与其标准值之差的实况和预报值的相关系数,一般取为在一定区域内(如全球或半球)的平均。
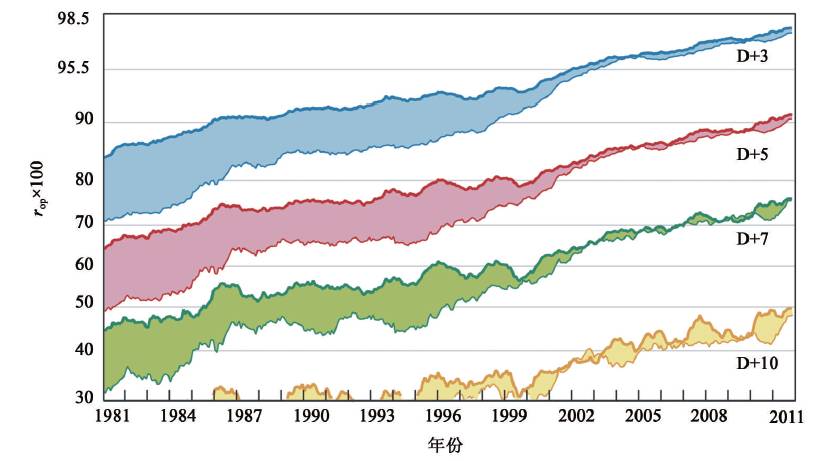
图4 ECMWF500hPa位势高度的预报能力逐年提高(纵坐标rop×100≥50 被认为预报可信。D+n 为第n天的预报。上下曲线各为北半球和南半球)
这种方法在世界各地和ECMWF同时发展和应用,而且模式的分辨率和物理过程的精细程度都已大为提高,其计算量之大则是“超级的”。好在电子计算机的进展能够与数值天气预报发展的速度同步,今天的数值预报已经变成数学物理理论和超级计算很好结合的成熟的巨大系统工程。
在全球中期天气预报发展的同时,区域性的短期天气数值预报也已发展到用更精细和分辨率更高的模式和四维同化方法,并把它嵌套到全球模式中去。图5 和图6 就是中国气象局做出的一个台风路径和强度预报及台风登陆时的天气形势预报图(钱传海和高拴柱提供)。
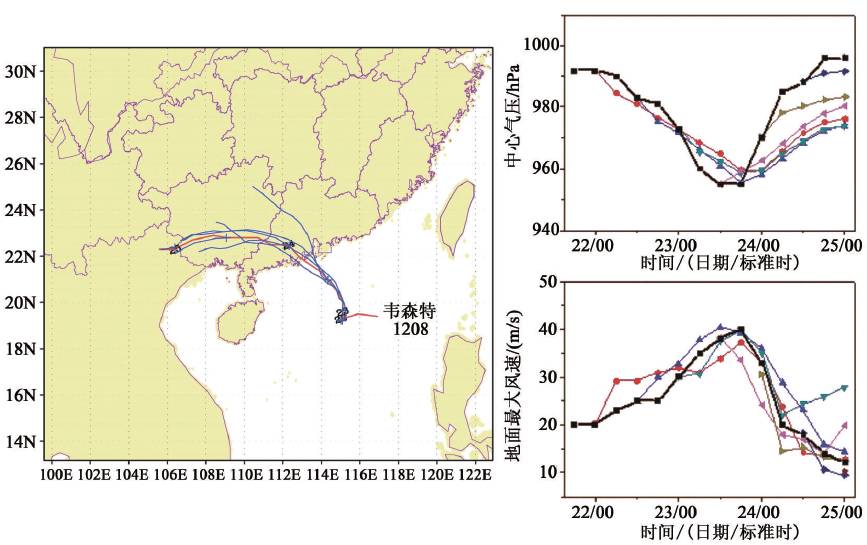
图5 2012 年韦森特(1208)台风路径(左图)和强度(右图)的24 小时预报(粗黑线为实况,其余是集合预报中的一些个例)
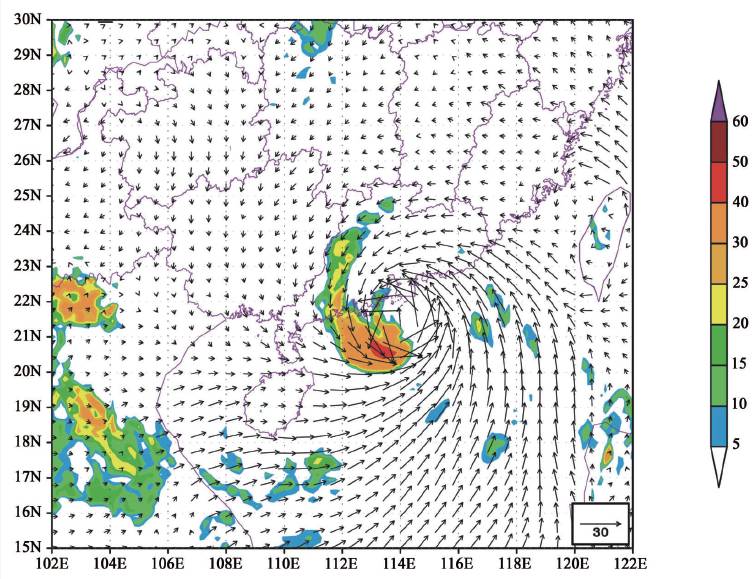
图6 韦森特(1208)台风登陆时的地面天气形势预报图(箭头为风速矢量,风速大小用线之长短表示。彩色为观测到的雷达回波强度,它越强则降雨越强)
数值天气预报已经成熟,其前景更辉煌。在前进的道路上,人们的需求将提出更多的有待解决的问题,而且受数值天气预报成功的鼓舞,气象预报也已逐步拓广到新领域中去了。
9.1 灾害天气及相关灾害的预报和防治
目前,对灾害天气还预报得不好。例如大多的暴雨的强度预报得太弱,甚至连落区都预报得不好;台风的预报精度也需提高;龙卷风和猛烈的雷暴对流及雷电过程还基本上无法预报。这些需要有更好的探测手段,也需要有针对性的特殊数值预报模式。至于由灾害天气引发的次生灾害,如山崩、泥石流和滑坡、林火、水库和河流溃坝等,也是更需要预报和防治的对象,为此需要建立相应的物理数学模式,与数值天气预报模式耦合起来。
9.2 探测网的完善和规划
不能想象,只用一个探测网就可以将所有要预报的天气现象“一网打尽”。其实,现有的探测网(包括其时空分布和探测的变量)是相当不完全和不够精确的,从而有漏网的和探测模糊的天气。因此,很自然就会提出这样的问题:为了在某地域和对某种危险的天气(例如台风和暴雨)预报好,应在何时何地做何种更精确的补充探测?这就是确定“观测目标区”问题,今已开始了研究,其本质上仍然是求优化问题,与求奇异向量和四维同化等的方法类似,但具体方法不同。
9.3 气候预测
作为数值天气预报的直接拓宽就是气候预测的动力学方法,或简称为动力学气候预测(dynamical climate prediction)或数值气候预测(numerical climate prediction)。它几乎与数值预报同时发展,也经历过从滤波模式(但计入与陆表和海表的热量交换)到全球原始方程模式等阶段,但由于其更为复杂和更为长期,短期气候预测至今只达到可准业务使用的阶段。
气候的成因和演变更为复杂,影响因素更多。首先,海洋(包括洋冰)和陆表层状态及其演变对大气中的气候有重大的影响,故预测气候,除大气环流模式外,还必须建立较好的大洋环流模式和陆表过程模式,并将大气环流模式与之耦合起来,这是一个更为复杂的模式系统。
海洋和陆表层的观测资料更为不足,四维同化就更显得重要。集合预测显然也是必须的。注意到气候预测的时段已完全超出初值问题的可预测时限,预测误差最主要的来源可能是模式自身的误差,故不能像中期天气数值预报那样,由初始场加小扰动产生集合,我国的经验是可用逐天做的预测作为集合,这是因为这样有前后一大串预报,它们合在一起,可在一定程度上反映模式误差导致的大范围较长期的流场系统间的相互作用。更长时段内的流场即气候系统(以别于天气系统),才是产生气候异常的主要载体。尽管如此,气候预测仍然还有较大的不确定度,需要由过去的样品集里找出一些统计特性来建立预报的订正系统。除此之外,不只给出数学期望,同时给出集合预测的离散度和某种气候型(例如多雨型)的概率,可能对用户更为有益,这是因为气候预测主要用于规划,而规划是可以有多种方案选择的。我国最早就是这样做的,现今世界上也大体这样做,大同小异。
9.4 气候与生态和环境系统的预测及调控
人们的居住和活动与其周围的生态和环境系统更为密切相关,这里的“生态”是指有生命活动的植物界(在这里称为“植被”)、动物界和微生物界的状态。它们和气候变化等一起,还有物种演替等的演变进展和灾害过程(如荒漠化、传染病和病虫害的发生和传播等过程)都是人类所关心的。人们在更长时期内的活动规划,尤其是为了可持续发展,正在要求对气候与生态和环境系统的变化做预测和调控规划。预测的需求不说自明,调控规划的例子如大规模改变自然环境、城市化和工业化、人类活动带来的排放和污染等等。总之,人们应如何顺应自然之理来合理规划自身的活动,使自然环境能承载人类的可持续发展。
现在,科学界已经在建立“气候与生态和环境系统模式”,或简称为“地球系统模式”(Earth system model)。大体上可归纳为7 个分系统模式,即大气环流模式(AGCM)、大洋环流加洋冰模式(OGCM+OICM)、陆表物理过程模式(LSM)、植被动力学模式(DGVM)、气溶胶和大气化学模式(AACM)、陆地生物地球化学模式(LBCM)和海洋生物地球化学模式(OBCM)及其耦合。这样的地球系统模式雏形虽已建立起来了,但对这样超大规模的系统模式的合理研制和模拟,对它演化过程的研究、预测和调控,还要求地球科学、数学、物理学以及化学和生物学界共同合作才能有成。
9.5 人工影响天气工程理论问题
人工影响天气(如增雨、消雹、消雾等)有巨大现实意义,其提出已有几十年历史,主要方法是通过在云雾中撒播催化剂来控制其中各态水滴的变化过程,以达到人们的目的。无疑,即使在现有方法和技术条件下,要达到目的,必须将观测、预报、作业方案和效果检验一体化,提成一个“自然控制论”问题,这里包括资料同化、适时和滚动方式预报和最优规划问题等,大约5 年后可变成可行的业务。至于更进一步的提高则要在催化材料和物理过程方面多下功夫,还要探索人工控制雷电的可能性,这些也都需要多学科共同努力。
致谢 本工作得到了中国气象局李泽椿院士与陈德辉、钱传海和高拴柱诸位数值天气预报专家提供的资料以及中国科学院大气物理研究所吴琳博士的协助,谨此致谢。
天气预报——由经验到物理数学理论和超级计算(一)
















